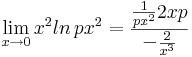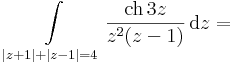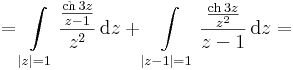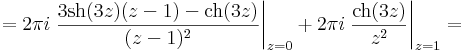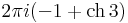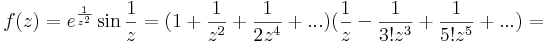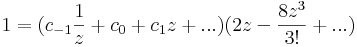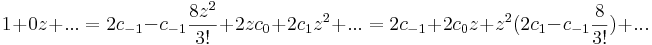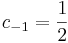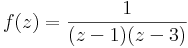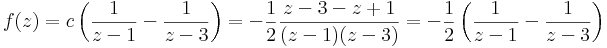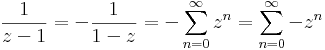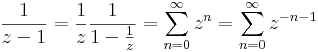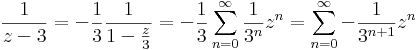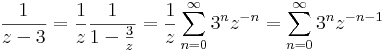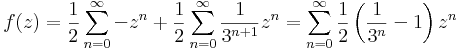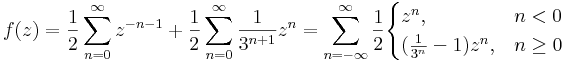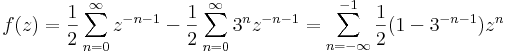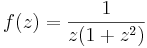A3 2009 gyak 2
Tartalomjegyzék |
Szeparábilis differenciálegyenlet
1. Oldjuk meg az
egyenletet az
- a)
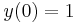
- b)
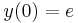
kezdeti feltételek mellett!
Mo. a) Az egyenlet konstans megoládsa az y(x)=1. Ez a kezdeti feltételnek megfelel.
b) Az általános megoldásból keressük a kezdeti feltételt kielégítő megoldást:
ez az implicit egyenlet. Ha x=0 és y=e, akkor
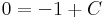 ,
, 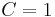
és
Megjegyzés. Minden R× R+-beli kezdeti feltételre egyértelműen létezik a megoldás.
Homogén fokszámú egyenlet
Azt mondjuk, hogy az y' = F(x,y) egyenlet homogén fokszámú, ha
A homogén fokszámú egyenlet megoldása visszavazethető a szeparálásra az
új változó bevezetésével, ahol u = u(x) az ismeretlen függvény. Tehát:
Ekkor
azaz
2. Oldjuk meg az
egyenletet! Mo. Általános megoldás:
A szinguláris megoldás: ha x0 = 0, akkor y szükségképpen 0. Itt viszont nem reguláris a differenciálegyenlet:
azaz a 0-hoz tart, így legalább kettő (valójában végtelen) megoldás halad át a (0,0) ponton.
Cauchy-típusú integrálok
3.
- a)
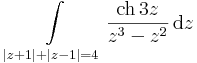
- (a görbe egy pozitívan irányított 0 középponttú ellipszis) és a
- b)
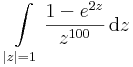
integrálokat!
- c) Milyen szakadások vannak z=0-ban?
- d) Adja meg a reziduumokat a z=0-ban!
Mo. a)
az első másodfokú pólus, a második tagban egy elsőfokú pólust fedezhtünk föl. A reziduumok az integrálok a 2 pi i-k nélkül.
b) A nullabeli 99. deriváltra van szükségünk:
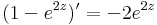 , n = 1
, n = 1
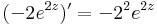 , n = 2
, n = 2
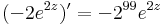 , n = 99
, n = 99
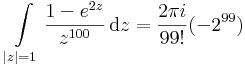 Ez egy 99-edfokú pólus, residuuma a 2pi i nélküli tényező.
Ez egy 99-edfokú pólus, residuuma a 2pi i nélküli tényező.
Reziduumszámítás
4. Számítsuk ki az alábbi függvények 0-beli reziduumát, egységkörön vett integrálját és a szakadás jellegét!
- a)
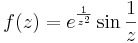
- b)
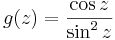
- c)
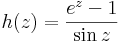
- d)
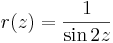
Mo.a)
Tehát Res=1
Lényeges szakadás.
c) Megszüntethető szakadású. Reguláris, res = 0
d) másodfokú pólus.
Laurent-sorfejtés
5. Határozzuk meg az
nulla körüli Laurent-sorait!
Mo.
alkalmas tehát a c=-1/2.
Ha |z|<1, akkor
Ha |z|>1, akkor
A másik tag:
Ha |z/3|<1, azaz |z|<3
Ha |z|>3 , akkor
Tehát a Laurent-sorok:
|z|<1 esetén reguláris:
1<|z|<3 esetén vegyes:
|z|>3 esetén csak főrész:
HF Fejtsük sorba a 0 körül az
függvényt!
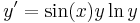
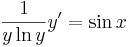
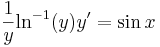
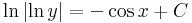
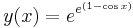
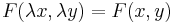
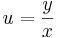
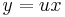
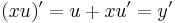
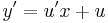
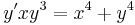
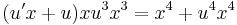
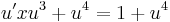
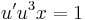
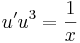
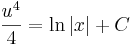
![u=\pm\sqrt[4]{4\mathrm{ln}\,|x|+4C}\,](/upload/math/9/2/c/92c828e446155e1571510d03bc9aa230.png)
![y=\pm x\sqrt[4]{\mathrm{ln}\,px^4}\,](/upload/math/c/5/2/c52a3cc885656d8c54e3886552790237.png)