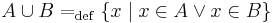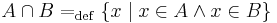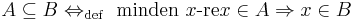Haladó szintre hozó kurzus/1
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Kijelentéslogika) |
Mozo (vitalap | szerkesztései) (→Kijelentéslogika) |
||
| 14. sor: | 14. sor: | ||
:c) <math>\neg (p\vee q)\quad \equiv\quad (\neg p)\wedge (\neg q),\qquad\neg(p\wedge q)\quad \equiv\quad (\neg p)\vee (\neg q)\qquad</math> (De-Morgan-szabályok) | :c) <math>\neg (p\vee q)\quad \equiv\quad (\neg p)\wedge (\neg q),\qquad\neg(p\wedge q)\quad \equiv\quad (\neg p)\vee (\neg q)\qquad</math> (De-Morgan-szabályok) | ||
:d) <math>(p\vee q)\wedge r\quad \equiv\quad (p \wedge r) \vee (q\wedge r),\qquad(p\wedge q)\vee r\quad \equiv\quad (p \vee r) \wedge (q\vee r)</math> (disztributív szabályok) | :d) <math>(p\vee q)\wedge r\quad \equiv\quad (p \wedge r) \vee (q\wedge r),\qquad(p\wedge q)\vee r\quad \equiv\quad (p \vee r) \wedge (q\vee r)</math> (disztributív szabályok) | ||
| + | |||
| + | ==Halmazok== | ||
| + | |||
| + | ''3.''' Tudva hogy: | ||
| + | :<math>A\cup B=_\mathrm{def}\{x\mid x\in A \vee x\in B\}</math> | ||
| + | :<math>A\cap B=_\mathrm{def}\{x\mid x\in A \wedge x\in B\}</math> | ||
| + | :<math>A\subseteq B\Leftrightarrow_\mathrm{def}\mbox{ minden }x\mbox{-re} x\in A \Rightarrow x\in B</math> | ||
| + | |||
A lap 2016. június 28., 21:24-kori változata
- Ez az szócikk a Haladó szintre hozó szócikk alszócikke.
Kijelentéslogika
1. Igazoljuk igazságtáblázattal, hogy a következő kijelentések mindig igazak:
- a)
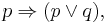
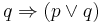 (a "vagy" alaptulajdonsága)
(a "vagy" alaptulajdonsága)
- b)
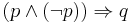 (a "hamisból" minden következik)
(a "hamisból" minden következik)
- c)
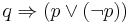 (az "igaz" mindenből következik)
(az "igaz" mindenből következik)
- d)
![[(p\Rightarrow r) \wedge (q\Rightarrow r)\wedge (p\vee q)]\Rightarrow r](/upload/math/a/f/6/af6a1f4b08d74a659f06d8ad51bd32e5.png) (az esetszétválasztás szabálya)
(az esetszétválasztás szabálya)
2. Igazoljuk igazságtáblázattal, hogy alább a ≡ két oldalán álló kifejezés mindig ugyanolyan igazságértékű!
- a)
![\neg(p\Rightarrow q)\quad \equiv\quad [(\neg q)\Rightarrow (\neg p)]\qquad](/upload/math/d/b/6/db67b43351e75f3dd2b823e8385f6084.png) (a kontrapozíció szabálya)
(a kontrapozíció szabálya)
- b)
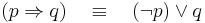 (a "ha-akkor" jellemzése "vagy"-gyal és "nem"-mel)
(a "ha-akkor" jellemzése "vagy"-gyal és "nem"-mel)
- c)
 (De-Morgan-szabályok)
(De-Morgan-szabályok)
- d)
 (disztributív szabályok)
(disztributív szabályok)
Halmazok
3.' Tudva hogy:
| Haladó szintre hozó | 2. téma |