Informatika1-2015
(→Latex Házi Még nem végleges, ma este még változik!!!) |
(→Pótlási lehetőségek) |
||
| (4 szerkesztő 73 közbeeső változata nincs mutatva) | |||
| 38. sor: | 38. sor: | ||
*** regex | *** regex | ||
*** olvassátok el a gyakorlati anyagokat a [[#Gyakorlatok|wiki]]-n! | *** olvassátok el a gyakorlati anyagokat a [[#Gyakorlatok|wiki]]-n! | ||
| − | * 9. hét, péntek, '''11.06. 14:00-15:00 K275''' | + | * 9. hét, péntek, '''11.06. 14:00-15:00 K275''' ([http://math.bme.hu/~kkovacs/info1/i1_15_ZH2_minta.pdf mintaZH] csak a feladatok mennyiségére példa, a gyakorló kérdéseket az elõadások végén találjátok) |
| − | * 14. hét, péntek, '''12.11. 14:00-15:00 K275''' | + | * 14. hét, péntek, '''12.11. 14:00-15:00 K275''' [[Informatika1-2015/OsszefoglaloZH3|Összefoglaló]] |
* RöpZH 10 alkalommal, a gyakorlatok elején (első héten természetesen nem lesz) | * RöpZH 10 alkalommal, a gyakorlatok elején (első héten természetesen nem lesz) | ||
| + | |||
| + | === Pótlási lehetőségek === | ||
| + | PóZH-k: | ||
| + | * december 16, szerda 14:00-15:00, H607 | ||
| + | * december 18, péntek 14:00-15:00, H607 (pótpót, jelentkezni kell a Neptuban) | ||
== Előadások == | == Előadások == | ||
| 52. sor: | 57. sor: | ||
[http://www.math.bme.hu/~wettl/okt/info1/2015/h04_15i1.pdf 4. előadás: Számok és karakterek] | [http://www.math.bme.hu/~wettl/okt/info1/2015/h04_15i1.pdf 4. előadás: Számok és karakterek] | ||
| − | [http://www.math.bme.hu/~wettl/okt/info1/2015/h05_15i1.pdf 5. előadás: WWW, HTML, CSS] | + | [http://www.math.bme.hu/~wettl/okt/info1/2015/h05_15i1.pdf 5. előadás: WWW, HTML, CSS (kérdésekkel frissítve 2011-11-03)] |
[http://www.math.bme.hu/~wettl/okt/info1/2015/h06_15i1.pdf 6-7. előadás: LaTeX alapjai] + egy [http://www.math.bme.hu/~wettl/okt/info1/2015/h08_15i1_prez.pdf prezentáció a prezentációról] a gyakorlathoz | [http://www.math.bme.hu/~wettl/okt/info1/2015/h06_15i1.pdf 6-7. előadás: LaTeX alapjai] + egy [http://www.math.bme.hu/~wettl/okt/info1/2015/h08_15i1_prez.pdf prezentáció a prezentációról] a gyakorlathoz | ||
| − | [http://www.math.bme.hu/~wettl/okt/info1/2015/h07_15i1_mat.pdf 8. előadás: Matematika szedése LaTeX-ben (V. 2015-10- | + | [http://www.math.bme.hu/~wettl/okt/info1/2015/h07_15i1_mat.pdf 8. előadás: Matematika szedése LaTeX-ben (V. 2015-11-03) kérdések frissítve] |
| + | |||
| + | [http://www.math.bme.hu/~wettl/okt/info1/2015/h09_15i1_octave.pdf 9. előadás: Mátrixalapú nyelvek -- octave (V. 2015-11-03)] | ||
| + | |||
| + | [http://www.math.bme.hu/~wettl/okt/info1/2015/Elso_gyors_tura.sws 10-11. előadás: Komputer algebra rendszerek -- sage (V. 2015-11-24)] [https://leibniz.math.bme.hu:8000/home/pub/5/ Link csak nézésre] | ||
| + | |||
| + | [http://www.math.bme.hu/~kkovacs/info1/i1_15_ea12.nb 12. előadás: Komputer algebra rendszerek -- Wolfram Mathematica (V. 2015-12-01)] [http://www.math.bme.hu/~kkovacs/info1/wolfram1.pdf Link csak nézésre] | ||
| + | |||
| + | [http://www.math.bme.hu/~kkovacs/info1/i1_15_ea13.nb 13. előadás: Komputer algebra rendszerek -- Wolfram Mathematica (V. 2015-12-01)] [http://www.math.bme.hu/~kkovacs/info1/i1_15_ea13.pdf Link csak nézésre] | ||
== Gyakorlatok == | == Gyakorlatok == | ||
| 68. sor: | 81. sor: | ||
* [[Informatika1-2015/Gyakorlat7|7. gyakorlat]] | * [[Informatika1-2015/Gyakorlat7|7. gyakorlat]] | ||
* [[Informatika1-2015/Gyakorlat8|8. gyakorlat]] | * [[Informatika1-2015/Gyakorlat8|8. gyakorlat]] | ||
| + | * [[Informatika1-2015/Gyakorlat9|9. gyakorlat]] ([[Informatika1-2015/Gyakorlat9megoldasok|megoldások]]) | ||
| + | * [[Informatika1-2015/Gyakorlat10|10. gyakorlat]] ([[Informatika1-2015/Gyakorlat10megoldasok|megoldások]]) | ||
| + | * [[Informatika1-2015/Gyakorlat11|11. gyakorlat]] ([[Informatika1-2015/Gyakorlat11megoldasok|megoldások]]) | ||
| + | * [[Informatika1-2015/Gyakorlat12|12. gyakorlat]] ([http://math.bme.hu/~kkovacs/info1/i1_15_gy12_megold.nb megoldások], [http://math.bme.hu/~kkovacs/info1/i1_15_gy12_megold.pdf pdf-ben]) | ||
| + | * [[Informatika1-2015/Gyakorlat13|13. gyakorlat]] (ezek csak a csütörtöki gyak után lesznek fent) | ||
== Házi feladatok == | == Házi feladatok == | ||
| 125. sor: | 143. sor: | ||
** [https://regex101.com/r/pR7gA1/3 link] | ** [https://regex101.com/r/pR7gA1/3 link] | ||
| − | ===HTML Házi feladat (12 pont)=== | + | === HTML Házi feladat (12 pont) === |
A feladat egy érvényes (https://validator.w3.org/ szerint a html, valamint https://jigsaw.w3.org/css-validator/ szerint a css fájl) HTML5 weboldal elkészítése. | A feladat egy érvényes (https://validator.w3.org/ szerint a html, valamint https://jigsaw.w3.org/css-validator/ szerint a css fájl) HTML5 weboldal elkészítése. | ||
A következőképp pontozunk: az első három pont kritérium, aki ezekből valamelyiket nem teljesíti, annak nem jár pont a többiért sem! | A következőképp pontozunk: az első három pont kritérium, aki ezekből valamelyiket nem teljesíti, annak nem jár pont a többiért sem! | ||
| 146. sor: | 164. sor: | ||
A plagizálást 0 ponttal honoráljuk! | A plagizálást 0 ponttal honoráljuk! | ||
| − | === Latex Házi | + | === Latex Házi === |
| − | + | Beadandó egy legalább 2.5, legfeljebb 3 oldalas LaTeX dokumentum. | |
| − | A | + | A dokumentum felépítése a következő legyen: |
| − | * néhány házi | + | * Az első fejezet álljon néhány, általatok előzőleg megoldott és beadott házi feladatból (analízis, algebra etc., 6 pont) |
| − | * matematikai képletek | + | ** terjedelme legalább egy oldal; |
| − | * táblázat vagy mátrix ( | + | ** kötelező a matematikai képletek használata (kiemelt és sorfolytonos)! |
| − | * beillesztett kép ( | + | * A dolgozat második fejezete rövid, tetszőleges matematikai témájú írás. Mindenképp használjuk a következőket: |
| − | * hivatkozás egy képletre, képre vagy hasonlóra a dokumentumban (\ref, \aref | + | ** legalább egy táblázat vagy mátrix (1 pont); |
| − | * | + | ** beillesztett kép (úszó ábraként, 1 pont); |
| − | * | + | ** hivatkozás egy képletre, képre vagy hasonlóra a dokumentumban (\ref, \aref stb., 1 pont); |
| − | '''Beadási határidő: 2015.11.08 23:59:59''', viszont erősen ajánlott a ZH előtt elkezdeni, gyakorlásnak tökéletes!!! | + | ** Legalább egy definíció és tétel (1-1 pont); |
| + | Az elérhető összpontszám '''12 pont'''. | ||
| + | Pontlevonás jár | ||
| + | * olvashatatlan a forráskódért (tagoljunk, ahol lehet); | ||
| + | * felesleges parancsok használatáért (pl. indokolatlan térköz); | ||
| + | * Nem megfelelő terjedelem esetén. | ||
| + | '''Beadási határidő: 2015.11.08 23:59:59''', viszont erősen ajánlott a ZH előtt elkezdeni, gyakorlásnak tökéletes! | ||
| + | |||
| + | === TikZ Házi === | ||
| + | * Fejezzük be a gyakorlaton elkezdett ábrát: [http://math.bme.hu/~kkovacs/info1/haromszog.pdf haromszog.pdf] (csak a végleges kell) | ||
| + | |||
| + | * Rajzoljunk egy analóg órát, pl: [http://download.rimelek.hu/php/AnalogOra/ora1.gif óra], elég az 5 perces közöket jelezni, nem kell minden percet. Legyen meg mind a 3 mutatója, látszódjon mindegyik és megfelelõ méretûek és más színûek legyenek. Az órának legyen egy fehértõl különbözõ alapszíne (pl a képen lilás kés). | ||
| + | |||
| + | * Körhöz, ellipszishez segítség: [http://cremeronline.com/LaTeX/minimaltikz.pdf minimaltikz.pdf], valamint ne felejtsétek el, hogy lehet használni '''sin''', '''cos''' függvényeket TikZ-ben. | ||
| + | '''Beadási határidő: 2015.11.13 23:59:59''' | ||
| + | |||
| + | ==== Tipikus hibák ==== | ||
| + | * A bekeretezett képlet a háromszög mellett. | ||
| + | |||
| + | NEM JÓ: | ||
| + | \draw (0,2) -- (0,3) node[pos=0.5,left]{$T=\frac{c\cdot m_c}{2}$} -- (-1.6,3) -- (-1.6,2) -- cycle; | ||
| + | JÓ: | ||
| + | \draw(-1,2)node[draw]{$T=\frac{c\cdot m_c}{2}$}; | ||
| + | |||
| + | * A zárt vonalakat, íveket zárjuk le <tt>--cycle</tt> paranccsal. | ||
| + | * A zöld szögtartomány belesüllyed a háromszög oldalaiba: [[http://math.bme.hu/~borbely/LaTeX/hiba1.png hiba1]]. | ||
| + | |||
| + | Egy lehetséges megoldás, hogy a kitöltött körívet és a feliratot a háromszög megrajzolása ELÉ tesszük: | ||
| + | \draw[fill=green](0,0)--(1,0)arc(0:59:1)--cycle; | ||
| + | \draw(0,0)--(4,0)node[pos=0.15,above]{$59^\circ$}; | ||
| + | \draw[ultra thick](0,0)--(4,0)--(3,5)--cycle; | ||
| + | |||
| + | Vagy legyen a háromszög oldala a szögtartománnyal egyenlő vastagságú: | ||
| + | \draw[thick](0,0)--(4,0)--(3,5)--cycle; | ||
| + | \draw[fill=green,thick](0,0)--(1,0)arc(0:59:1)--cycle; | ||
| + | \draw(0,0)--(4,0)node[pos=0.15,above]{$59^\circ$}; | ||
| + | |||
| + | Ez végül is nem hiba, feltéve hogy direkt ez volt a megoldó szándéka. | ||
| + | |||
| + | * Az óra számlapján a számjegyek megadása a rovátka helyéhez viszonyítva. Polár koordinátákat érdemes használni. | ||
| + | NEM JÓ: | ||
| + | \draw (cos{60}*1.7,sin{60}*1.7) node[below left]{1} -- (cos{60}*2,sin{60}*2); | ||
| + | \draw (cos{30}*1.7,sin{30}*1.7) node[below left]{2} -- (cos{30}*2,sin{30}*2); | ||
| + | \draw (2,0) -- (1.7,0) node[left]{3}; | ||
| + | . | ||
| + | . | ||
| + | . | ||
| + | Érdemesebb a számjegyeket egy kisebb sugarú körön elhelyezni és <tt>\foreach</tt> parancsot használni: | ||
| + | |||
| + | JÓ: | ||
| + | \foreach \hour in {1,2,...,12} | ||
| + | { | ||
| + | \draw ({90-\hour*30}:2) -- ({90-\hour*30}:1.8); | ||
| + | \draw ({90-\hour*30}:1.5) node{$\hour$}; | ||
| + | } | ||
| + | * A számlapon a számjegyeket érdemes math módba tenni (<tt>$1$</tt>). Ez nem kötelező, inkább ajánlás. Én a háromszög csúcsait is inkább így nevezném el: <tt>$A$</tt>, <tt>$B$</tt>, <tt>$C$</tt>. | ||
| + | * Az óra közepén a fekete pontra ez nem jó: | ||
| + | \draw (0,0) node{$\bullet$}; | ||
| + | helyette mondjuk: | ||
| + | \filldraw (0,0) circle(0.1); | ||
| + | És szebb ha a mutatókat rajzoljuk ki először és utána a pontot, mert akkor fedi a mutatókat. | ||
| + | |||
| + | ==== Egy megoldás az órás feladatra ==== | ||
| + | Egy saját megoldás az órára, ami a fordításkori időt mutatja: [[http://math.bme.hu/~borbely/LaTeX/T0_HF4_borbely.tex pontos idő]]. A stílust ''Gál Kristóf''tól vettem. | ||
| + | |||
| + | === Octave === | ||
| + | Adjunk meg <tt>octave</tt>-ban egy | ||
| + | x = megoldas(n,c) | ||
| + | alakban hívható függvényt, ami megadja egy <math>n</math>-ismeretlenes lineáris egyenletrendszer egy megoldását. Ez az egyenletrendszer <math>n=6</math> esetén a következő alakot ölti: | ||
| + | A*x = [1; 1; 1; 1; 1; 1] | ||
| + | ahol | ||
| + | A = | ||
| + | -1.0 1.0 0.0 0.0 0.0 0.0 | ||
| + | -0.5 0.0 0.5 0.0 0.0 0.0 | ||
| + | 0.0 -0.5 0.0 0.5 0.0 0.0 | ||
| + | 0.0 0.0 -0.5 0.0 0.5 0.0 | ||
| + | 0.0 0.0 0.0 -0.5 0.0 0.5 | ||
| + | 0.0 0.0 0.0 0.0 -1.0 1.0 | ||
| + | Az első argumentumban megadott <math>n</math> változótól függjön az <tt>A</tt> mátrix mérete (<math>n\times n</math>-es) és egyben a jobb oldali vektor mérete is (<math>n\times1</math>-es)!<br> | ||
| + | Az <tt>A</tt> mátrix rangja <math>n - 1</math> (tesztelés közben ellenőrizzük), így nulltere 1-dimenziós, tehát az összes megoldás <math>x_0+cy</math> alakba írható, ahol <math>x_0</math> az egyetlen sortérbe eső megoldás, <math>y</math> pedig a nullteret kifeszítő vektor. A függvény tehát az <math>(n,c)</math> bemenetre az <math>x_0+cy</math> megoldást adja vissza. | ||
| + | |||
| + | Segítség: | ||
| + | * Az <tt>A</tt> mátrix nem invertálható, de a beépített balról osztás műveletével ('''<tt>\</tt>''') épp az egyetlen sortérbe eső megoldást kapjuk meg. | ||
| + | * A nulltér meghatározásához használhatjátok a <tt>null</tt> parancsot! | ||
| + | |||
| + | Formai követelmények: | ||
| + | * A megoldást egy <tt>.m</tt> kiterjesztésű szövegfájlban küldjétek el. | ||
| + | * A fájl a feladatban kitűzött egyetlen függvény definícióját tartalmazza és semmi mást | ||
| + | * A fájl végén legyen egy üres sor. | ||
| + | * A fájl neve a következő formátumú legyen: | ||
| + | T<tankör>_HF5_<account>.m | ||
| + | |||
| + | '''Beadási határidő: dec. 1. 23:59:59, 3 pont''' | ||
| + | |||
| + | Tanács: | ||
| + | * A <tt>megoldas</tt> függvény belsejében minden parancsot pontosvesszővel ('''<tt>;</tt>''') zárjunk le. | ||
| + | * Érdemes [[Putty_haszn%C3%A1lata|Putty]]-al belépni a <tt>leibniz</tt>-re és ott használni az <tt>octave</tt>-ot és [[WinScp_haszn%C3%A1lata|WinScp]]-vel szerkeszteni a beküldendő fájlt. | ||
| + | * Teszteléshez használhatjuk az <tt>octave</tt>-ot parancssorból így: | ||
| + | borbely@leibniz:~$ <b>octave T9_HF5_borbely.m</b> | ||
| + | |||
| + | Egy megoldás: | ||
| + | function x=megoldas(n,c) | ||
| + | A=[-1 1 zeros(1,n-2); (diag(0.5*ones(n-1,1),1)-diag(0.5*ones(n-1,1),-1))(2:n-1,:); zeros(1,n-2) -1 1]; | ||
| + | x=A\ones(n,1)+null(A)*c; | ||
| + | endfunction | ||
| + | |||
| + | === Sage === | ||
| + | |||
| + | A feladatokat a [http://sage.math.bme.hu Sage]-en oldjátok meg. | ||
| + | |||
| + | A kész házit úgy tudjátok elküldeni, ha lementitek a worksheetet: bal fent ''File...'' -> ''Save worksheet to a file...'', majd csatoljátok az így lementett file-t emailben, a két feladat megoldását küldhetitek egy worksheet-ben. | ||
| + | |||
| + | ==== 1. feladat (2 pont) ==== | ||
| + | |||
| + | A következõ mátrixok adottak (ahol ''x'' egy szimbolikus változó): | ||
| + | X = x 1 | ||
| + | 1 x | ||
| + | |||
| + | Y = 2 x | ||
| + | -1 -1 | ||
| + | |||
| + | Z = -1 2 | ||
| + | x 2 | ||
| + | |||
| + | keressük, meg, hogy milyen ''x'' értékekre lesznek az alábbi blokkmátrixok invertálhatók: | ||
| + | A = X X | ||
| + | X X | ||
| + | |||
| + | B = X Y | ||
| + | Y X | ||
| + | |||
| + | C = X Z | ||
| + | Y Z | ||
| + | |||
| + | A C mátrix determinánsa egy polinom x-ben. Ábrázoljuk a [-3,2] intervallumon! | ||
| + | |||
| + | ==== 2. feladat (1 pont) ==== | ||
| + | |||
| + | Generáljuk le az összes olyan [https://hu.wikipedia.org/wiki/Pitagoraszi_sz%C3%A1mh%C3%A1rmasok pithagoraszi számhármas] listáját, ahol mindhárom szám kisebb mint száz és legalább az egyik szám prím! (Segítség: ''and'' és ''or''-t használjatok a logikai kifejezésekhez) | ||
| + | '''Beadási határidő: dec. 10. 23:59:59''' (A ZH-ra jó készülésnek.) | ||
| + | |||
| + | === Wolfram Mathematica === | ||
| + | A beadandó házi feladat a 13. gyakorlat feladatai közül a 24. (2 pont) és a 25. (1 pont). | ||
| + | * 24. feladatban érdemes a <tt>NestWhileList</tt> parancsot nézegetni | ||
| + | * 25. feladatban érdemes a <tt>Relpace</tt> és <tt>RelpaceAll</tt> (<tt>/.</tt>) parancsokat nézegetni | ||
| + | Beadási határidő: '''2015.12.17. 23:59:59''' | ||
| + | |||
| + | A szokásos levélben mellékeljetek egy Mathematica notebook-ot a szokásos névkonvencióval (<tt>tankör_HF7_felhasználó.nb</tt>). | ||
== Hasznos dolgok == | == Hasznos dolgok == | ||
* [http://techsalsa.com/wp-content/uploads/2009/03/us_keyboard_layout.png Angol billentyűzet kiosztás] | * [http://techsalsa.com/wp-content/uploads/2009/03/us_keyboard_layout.png Angol billentyűzet kiosztás] | ||
A lap jelenlegi, 2015. december 14., 09:46-kori változata
Tartalomjegyzék |
Általános információk
- Előadó
- dr. Wettl Ferenc: wettl
- Gyakorlatok:
- Borbély Gábor: borbely
- Kovács Kristóf: kkovacs
- Nyíri Dávid Ákos: nyida
Minden matekos hallgatónak és dolgozónak van egy alanyi jogon járó honlapja és email címe:
- A valaki felhasználónak
- email: valaki@math.bme.hu
- honlap: math.bme.hu/~valaki
- Az előadás időpontja és helye
- Kedd 10:15-11:00 H406
- Gyakorlatok
- Kedd 11:15-13:00 H507
- Csütörtök 12:15-14:00 H507
- Csütörtök 14:15-16:00 H507
Laborhasználat
A H507-es labor belépőkártyás, a gyakorlatok alatt nyitva lesz a terem. Aki szeretné órán kívül használni a gépeket, az tud igényelni kártyát Elekné Barna Ibolyánál 2000Ft letét ellenében. A kártyákat a félév végeztével, vagy ha már nem kell, akkor adjátok vissza. A labor használat csak egy lehetőség a sok közül, saját gépen és távoli eléréssel is lehet dolgozni, ebben igény szerint segítünk.
ZH időpontok és helyek
- 5. hét, péntek, 10.09. 14:00-15:00 K275
- első 4 előadás anyaga
- hardver, operációs rendszer, absztrakt gépek, számábrázolás, karakterkódolás
- előadás végén összegyűjtött kérdések és azokhoz hasonlók
- olvassátok végig az előadás diák-at!
- első 3 gyakorlat anyaga
- alapvető bash parancsok
- regex
- olvassátok el a gyakorlati anyagokat a wiki-n!
- első 4 előadás anyaga
- 9. hét, péntek, 11.06. 14:00-15:00 K275 (mintaZH csak a feladatok mennyiségére példa, a gyakorló kérdéseket az elõadások végén találjátok)
- 14. hét, péntek, 12.11. 14:00-15:00 K275 Összefoglaló
- RöpZH 10 alkalommal, a gyakorlatok elején (első héten természetesen nem lesz)
Pótlási lehetőségek
PóZH-k:
- december 16, szerda 14:00-15:00, H607
- december 18, péntek 14:00-15:00, H607 (pótpót, jelentkezni kell a Neptuban)
Előadások
3. előadás: Operációs rendszerek
4. előadás: Számok és karakterek
5. előadás: WWW, HTML, CSS (kérdésekkel frissítve 2011-11-03)
6-7. előadás: LaTeX alapjai + egy prezentáció a prezentációról a gyakorlathoz
8. előadás: Matematika szedése LaTeX-ben (V. 2015-11-03) kérdések frissítve
9. előadás: Mátrixalapú nyelvek -- octave (V. 2015-11-03)
10-11. előadás: Komputer algebra rendszerek -- sage (V. 2015-11-24) Link csak nézésre
12. előadás: Komputer algebra rendszerek -- Wolfram Mathematica (V. 2015-12-01) Link csak nézésre
13. előadás: Komputer algebra rendszerek -- Wolfram Mathematica (V. 2015-12-01) Link csak nézésre
Gyakorlatok
- 1. gyakorlat
- 2. gyakorlat
- 3. gyakorlat
- 4. gyakorlat
- 5. gyakorlat
- 6. gyakorlat
- 7. gyakorlat
- 8. gyakorlat
- 9. gyakorlat (megoldások)
- 10. gyakorlat (megoldások)
- 11. gyakorlat (megoldások)
- 12. gyakorlat (megoldások, pdf-ben)
- 13. gyakorlat (ezek csak a csütörtöki gyak után lesznek fent)
Házi feladatok
A házi feladatok beadásának határideje minden esetben a gyakorlat előtti nap éjfél.
Szabályok: Lehet a házi feladatokról beszélni, konzultálni bárkivel, együtt készülni, tanulni. Nem szabad más kódját elkérni, átvenni, elolvasni, sajátként beküldeni. Mindenkinek a saját házi feladatát magának kell megírnia és beküldenie! A saját loginnevét és jelszavát senki nem adhatja át másnak!
Az emailben beadott házi feladatokat az info1hazi KUKAC gmail PONT com cimre várjuk. Mindenki a házi feladatát a matematika intézeti (user@math.bme.hu) email címéről küldje be a könnyebb azonossíthatóság kedvéért! Más címről érkező házi feladatot nem áll módunkban kijavítani!
A levél tárgya a következő formátumú legyen:
- <tankör>_HF<a feladat száma>_<felhasználói név>
Tehát ha pl. a T2 tankör kovacspisti loginnevű hallgatójának 3. házijához az email tárgya
- T2_HF3_kovacspisti
Csatolt fájlok esetén is ezt a konvenciót használjátok. (Pl. "T2_HF3_kovacspisti.txt", "T2_HF3_kovacspisti2.txt"...)
Egyéb levelek tárgyának elejére kerüljön a <tankör>_<felhasználói név>, majd utána a valódi tárgy, pl.
- T3_szabomari nem működik a szerver
Ha a házi feladatok javításával kapcsolatban kérdésetek van, azt is az info1hazi KUKAC gmail PONT com címre írjátok.
RegEx
3 pont, határidő 2015.09.30, 23:59:59
- a. Írjunk reguláris kifejezést, amely az angol mm/dd/yyyy formátumó dátumokat átírja yyyy.mm.dd formába! A kifejezést /regex/csere/ alakban küldjük be, ahol a regex az illeszkedő (Regular Expression), a csere pedig a Substitution sztring! (1 pont)
Minta szöveg, amire illeszkedni kell:
09/11/2001
Amire cserélni kéne:
2001.09.11
- b. Válogassuk ki egy Linux terminál utasításból kizárólag a parancsokat! Ehhez illesszünk reguláris kifejezést a parancs1 -arg11 arg21 ... | parancs2 arg21 arg22 ... | ... > file1 formátumú parancsokra (nem kell ellenőrizni, hogy értelmes-e, csak a formátumot), majd a Substitution sztringet formáljuk meg úgy, hogy az a parancs1 parancs2 ... parancs_n sztringet adja vissza! Használjuk a g kapcsolót! (2 pont)
Minta szöveg, amire illeszkedni kell:
cat ezmeg.az | grep "azta" | sort -n > ez.txt
Amire cserélni kéne:
cat grep sort
Megoldás
- a. Ez viszonylag egyértelmű volt: /(\d{2})\/(\d{2})\/(\d{4})/\3\.\1\.\2/, vagyis:
- regex:
(\d{2})\/(\d{2})\/(\d{4}) - csere:
\3\.\1\.\2
- regex:
- b. egy viszonylag jó megoldás: /(\"[^\"]+\"|[^\|\>\<\:\s\"]+)([^\|\<\>\n\r]*)(\||\>.*)?/\1/, vagyis:
- regex:
(\"[^\"]+\"|[^\|\>\<\:\s\"]+)([^\|\<\>\n\r]*)(\||\>.*)?
- csere:
\1
- g kapcsolóval
- link
- regex:
HTML Házi feladat (12 pont)
A feladat egy érvényes (https://validator.w3.org/ szerint a html, valamint https://jigsaw.w3.org/css-validator/ szerint a css fájl) HTML5 weboldal elkészítése. A következőképp pontozunk: az első három pont kritérium, aki ezekből valamelyiket nem teljesíti, annak nem jár pont a többiért sem! Az oldal a www.math.bme.hu/~user/info1hazi.html oldalon legyen elérhető! A forrás html és css fájlokat ezzel együtt el kell küldeni az info1hazi@gmail.com címre a fent említett módon!
- HTML5 valid oldal (1 pont)
- Külön CSS fájl, stíluselemek definíciójával (1 pont)
- Nem véletlenszerűen generált, értelmes tartalom (1 pont)
Egyéb szerezhető pontok:
- Többféle címsor (1 pont)
- Linkek használata (több külső- és belső link) (1 pont)
- CSS selectorok használata (class és id egyaránt, 1 pont)
- Táblázat (legalább 12 cella, 1 pont)
- Összetett táblázat, összevont sorok, oszlopok, formázott cellák (1 pont)
- Több aloldal, navigációval, esetleg menüvel (2 pont)
- Ízléses stílus (1 pont)
- Képek (lokális és globális URL-lel hivatkozva, 1 pont)
Beadási határidő:
- 1. tankör - 2015.10.19 23:59:59
- 2. és 3. tankör - 2015.10.21. 23:59:59
A plagizálást 0 ponttal honoráljuk!
Latex Házi
Beadandó egy legalább 2.5, legfeljebb 3 oldalas LaTeX dokumentum. A dokumentum felépítése a következő legyen:
- Az első fejezet álljon néhány, általatok előzőleg megoldott és beadott házi feladatból (analízis, algebra etc., 6 pont)
- terjedelme legalább egy oldal;
- kötelező a matematikai képletek használata (kiemelt és sorfolytonos)!
- A dolgozat második fejezete rövid, tetszőleges matematikai témájú írás. Mindenképp használjuk a következőket:
- legalább egy táblázat vagy mátrix (1 pont);
- beillesztett kép (úszó ábraként, 1 pont);
- hivatkozás egy képletre, képre vagy hasonlóra a dokumentumban (\ref, \aref stb., 1 pont);
- Legalább egy definíció és tétel (1-1 pont);
Az elérhető összpontszám 12 pont. Pontlevonás jár
- olvashatatlan a forráskódért (tagoljunk, ahol lehet);
- felesleges parancsok használatáért (pl. indokolatlan térköz);
- Nem megfelelő terjedelem esetén.
Beadási határidő: 2015.11.08 23:59:59, viszont erősen ajánlott a ZH előtt elkezdeni, gyakorlásnak tökéletes!
TikZ Házi
- Fejezzük be a gyakorlaton elkezdett ábrát: haromszog.pdf (csak a végleges kell)
- Rajzoljunk egy analóg órát, pl: óra, elég az 5 perces közöket jelezni, nem kell minden percet. Legyen meg mind a 3 mutatója, látszódjon mindegyik és megfelelõ méretûek és más színûek legyenek. Az órának legyen egy fehértõl különbözõ alapszíne (pl a képen lilás kés).
- Körhöz, ellipszishez segítség: minimaltikz.pdf, valamint ne felejtsétek el, hogy lehet használni sin, cos függvényeket TikZ-ben.
Beadási határidő: 2015.11.13 23:59:59
Tipikus hibák
- A bekeretezett képlet a háromszög mellett.
NEM JÓ:
\draw (0,2) -- (0,3) node[pos=0.5,left]{$T=\frac{c\cdot m_c}{2}$} -- (-1.6,3) -- (-1.6,2) -- cycle;
JÓ:
\draw(-1,2)node[draw]{$T=\frac{c\cdot m_c}{2}$};
- A zárt vonalakat, íveket zárjuk le --cycle paranccsal.
- A zöld szögtartomány belesüllyed a háromszög oldalaiba: [hiba1].
Egy lehetséges megoldás, hogy a kitöltött körívet és a feliratot a háromszög megrajzolása ELÉ tesszük:
\draw[fill=green](0,0)--(1,0)arc(0:59:1)--cycle;
\draw(0,0)--(4,0)node[pos=0.15,above]{$59^\circ$};
\draw[ultra thick](0,0)--(4,0)--(3,5)--cycle;
Vagy legyen a háromszög oldala a szögtartománnyal egyenlő vastagságú:
\draw[thick](0,0)--(4,0)--(3,5)--cycle;
\draw[fill=green,thick](0,0)--(1,0)arc(0:59:1)--cycle;
\draw(0,0)--(4,0)node[pos=0.15,above]{$59^\circ$};
Ez végül is nem hiba, feltéve hogy direkt ez volt a megoldó szándéka.
- Az óra számlapján a számjegyek megadása a rovátka helyéhez viszonyítva. Polár koordinátákat érdemes használni.
NEM JÓ:
\draw (cos{60}*1.7,sin{60}*1.7) node[below left]{1} -- (cos{60}*2,sin{60}*2);
\draw (cos{30}*1.7,sin{30}*1.7) node[below left]{2} -- (cos{30}*2,sin{30}*2);
\draw (2,0) -- (1.7,0) node[left]{3};
.
.
.
Érdemesebb a számjegyeket egy kisebb sugarú körön elhelyezni és \foreach parancsot használni:
JÓ:
\foreach \hour in {1,2,...,12}
{
\draw ({90-\hour*30}:2) -- ({90-\hour*30}:1.8);
\draw ({90-\hour*30}:1.5) node{$\hour$};
}
- A számlapon a számjegyeket érdemes math módba tenni ($1$). Ez nem kötelező, inkább ajánlás. Én a háromszög csúcsait is inkább így nevezném el: $A$, $B$, $C$.
- Az óra közepén a fekete pontra ez nem jó:
\draw (0,0) node{$\bullet$};
helyette mondjuk:
\filldraw (0,0) circle(0.1);
És szebb ha a mutatókat rajzoljuk ki először és utána a pontot, mert akkor fedi a mutatókat.
Egy megoldás az órás feladatra
Egy saját megoldás az órára, ami a fordításkori időt mutatja: [pontos idő]. A stílust Gál Kristóftól vettem.
Octave
Adjunk meg octave-ban egy
x = megoldas(n,c)
alakban hívható függvényt, ami megadja egy n-ismeretlenes lineáris egyenletrendszer egy megoldását. Ez az egyenletrendszer n = 6 esetén a következő alakot ölti:
A*x = [1; 1; 1; 1; 1; 1]
ahol
A = -1.0 1.0 0.0 0.0 0.0 0.0 -0.5 0.0 0.5 0.0 0.0 0.0 0.0 -0.5 0.0 0.5 0.0 0.0 0.0 0.0 -0.5 0.0 0.5 0.0 0.0 0.0 0.0 -0.5 0.0 0.5 0.0 0.0 0.0 0.0 -1.0 1.0
Az első argumentumban megadott n változótól függjön az A mátrix mérete (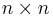 -es) és egyben a jobb oldali vektor mérete is (
-es) és egyben a jobb oldali vektor mérete is (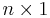 -es)!
-es)!
Az A mátrix rangja n − 1 (tesztelés közben ellenőrizzük), így nulltere 1-dimenziós, tehát az összes megoldás x0 + cy alakba írható, ahol x0 az egyetlen sortérbe eső megoldás, y pedig a nullteret kifeszítő vektor. A függvény tehát az (n,c) bemenetre az x0 + cy megoldást adja vissza.
Segítség:
- Az A mátrix nem invertálható, de a beépített balról osztás műveletével (\) épp az egyetlen sortérbe eső megoldást kapjuk meg.
- A nulltér meghatározásához használhatjátok a null parancsot!
Formai követelmények:
- A megoldást egy .m kiterjesztésű szövegfájlban küldjétek el.
- A fájl a feladatban kitűzött egyetlen függvény definícióját tartalmazza és semmi mást
- A fájl végén legyen egy üres sor.
- A fájl neve a következő formátumú legyen:
T<tankör>_HF5_<account>.m
Beadási határidő: dec. 1. 23:59:59, 3 pont
Tanács:
- A megoldas függvény belsejében minden parancsot pontosvesszővel (;) zárjunk le.
- Érdemes Putty-al belépni a leibniz-re és ott használni az octave-ot és WinScp-vel szerkeszteni a beküldendő fájlt.
- Teszteléshez használhatjuk az octave-ot parancssorból így:
borbely@leibniz:~$ octave T9_HF5_borbely.m
Egy megoldás:
function x=megoldas(n,c) A=[-1 1 zeros(1,n-2); (diag(0.5*ones(n-1,1),1)-diag(0.5*ones(n-1,1),-1))(2:n-1,:); zeros(1,n-2) -1 1]; x=A\ones(n,1)+null(A)*c; endfunction
Sage
A feladatokat a Sage-en oldjátok meg.
A kész házit úgy tudjátok elküldeni, ha lementitek a worksheetet: bal fent File... -> Save worksheet to a file..., majd csatoljátok az így lementett file-t emailben, a két feladat megoldását küldhetitek egy worksheet-ben.
1. feladat (2 pont)
A következõ mátrixok adottak (ahol x egy szimbolikus változó):
X = x 1
1 x
Y = 2 x
-1 -1
Z = -1 2
x 2
keressük, meg, hogy milyen x értékekre lesznek az alábbi blokkmátrixok invertálhatók:
A = X X
X X
B = X Y
Y X
C = X Z
Y Z
A C mátrix determinánsa egy polinom x-ben. Ábrázoljuk a [-3,2] intervallumon!
2. feladat (1 pont)
Generáljuk le az összes olyan pithagoraszi számhármas listáját, ahol mindhárom szám kisebb mint száz és legalább az egyik szám prím! (Segítség: and és or-t használjatok a logikai kifejezésekhez) Beadási határidő: dec. 10. 23:59:59 (A ZH-ra jó készülésnek.)
Wolfram Mathematica
A beadandó házi feladat a 13. gyakorlat feladatai közül a 24. (2 pont) és a 25. (1 pont).
- 24. feladatban érdemes a NestWhileList parancsot nézegetni
- 25. feladatban érdemes a Relpace és RelpaceAll (/.) parancsokat nézegetni
Beadási határidő: 2015.12.17. 23:59:59
A szokásos levélben mellékeljetek egy Mathematica notebook-ot a szokásos névkonvencióval (tankör_HF7_felhasználó.nb).