Informatika1-2016/HF5
(→Octave házi feladat) |
|||
| 33. sor: | 33. sor: | ||
* Érdemes [[Putty_haszn%C3%A1lata|Putty]]-al belépni a <tt>leibniz</tt>-re és ott használni az <tt>octave</tt>-ot és [[WinScp_haszn%C3%A1lata|WinScp]]-vel szerkeszteni a beküldendő fájlt. | * Érdemes [[Putty_haszn%C3%A1lata|Putty]]-al belépni a <tt>leibniz</tt>-re és ott használni az <tt>octave</tt>-ot és [[WinScp_haszn%C3%A1lata|WinScp]]-vel szerkeszteni a beküldendő fájlt. | ||
* Teszteléshez használhatjuk az <tt>octave</tt>-ot parancssorból így: | * Teszteléshez használhatjuk az <tt>octave</tt>-ot parancssorból így: | ||
| + | borbely@leibniz:~$ <b>octave T9_HF5_borbely.m</b> | ||
| + | |||
| + | == Másik lehetőség == | ||
| + | |||
| + | Mielőtt a beadandó házi feladat megoldásához kezdenétek, végezzétek el a következő lépéseket, melyek segítenek a feladat megoldásában! | ||
| + | |||
| + | Adjatok pozitív egész értéket egy változónak, pl. | ||
| + | >> n = 4 | ||
| + | Nézzétek meg mi történik a pascal(n) és a pascal(n,-1) parancsok hatására! Állítsatok elő egy $n\times(2n)$ méretű mátrixot, melynek első blokkja egy Pascal-háromszög (alsó háromszögmátrix), mellette egy egységmátrix, azaz például $n=4$ esetén | ||
| + | 1 0 0 0 1 0 0 0 | ||
| + | 1 1 0 0 0 1 0 0 | ||
| + | 1 2 1 0 0 0 1 0 | ||
| + | 1 3 3 1 0 0 0 1 | ||
| + | Nevezzétek el e mátrixot P-nek. Ezután képezzetek egy <math>n</math>-dimenziós b vektort, melynek elemei 2-hatvány plusz 1 alakúak <math>2^0+1</math>-től indulva, például esetünkben | ||
| + | 2 | ||
| + | 3 | ||
| + | 5 | ||
| + | 9 | ||
| + | Aki kicsit utánaszámol, láthatja, hogy a <math>\mathbf{Px}=\mathbf b</math> egyenletrendszer megoldható, egy megoldása a csupa 1-esből álló vektor. Határozzátok meg ennek a sortérbe eső egyetlen megoldását (mátrixosztás!). Az összes megoldáshoz meg kell még határozni a nullteret kifeszítő vektorokat. Ezt az octave a | ||
| + | null(P) | ||
| + | paranccsal megadja. | ||
| + | |||
| + | Végül a '''beadandó feladat''': Írjatok egy függvényt, melynek egyetlen paramétere <math>n</math>, és amely válaszul kiírja a fenti egyenletrendszer egyetlen sortérbe eső megoldását és a nullteret generáló vektorok mátrixát abban az esetben, ha <math>n<8</math>! Ha <math>n\ge8</math>, a program csak annyit írjon ki, hogy "Túl nagy adat!". Például <math>n=4</math> esetén | ||
| + | 1.3333e+00 | ||
| + | 1.3333e+00 | ||
| + | 1.0000e+00 | ||
| + | 3.3333e-01 | ||
| + | 6.6667e-01 | ||
| + | 3.3333e-01 | ||
| + | 4.4409e-16 | ||
| + | 3.3333e-01 | ||
| + | |||
| + | -0.616696 -0.106047 -0.043625 0.021813 | ||
| + | 0.399665 -0.409452 -0.144854 -0.010906 | ||
| + | -0.165320 0.570204 -0.172812 -0.163594 | ||
| + | -0.067442 -0.293872 0.778499 -0.389249 | ||
| + | 0.616696 0.106047 0.043625 -0.021813 | ||
| + | 0.217031 0.515499 0.188479 -0.010906 | ||
| + | -0.017314 0.354746 0.506146 0.163594 | ||
| + | -0.018896 -0.082339 0.218125 0.890937 | ||
| + | Formai követelmények: | ||
| + | * A megoldást egy <tt>.m</tt> kiterjesztésű szövegfájlban küldjétek el. Igyekezzetek a szövegfájlt a program értelme szerint formázni 2 szóközzel beljebb húzva a sorokat (ez nem kötelező). Például így: | ||
| + | function ... | ||
| + | if ... | ||
| + | ... | ||
| + | else | ||
| + | ... | ||
| + | endif | ||
| + | endfunction | ||
| + | |||
| + | * A fájl a feladatban kitűzött egyetlen függvény definícióját tartalmazza és semmi mást! (pl. ne legyen benne prompt sem, azaz >>) | ||
| + | * A fájl végén legyen egy üres sor. | ||
| + | * A fájl neve a következő formátumú legyen: | ||
| + | T<tankör>_HF5_<felhasználónév>.m | ||
| + | |||
| + | '''Beadási határidő: TBD''' | ||
| + | |||
| + | Tanács: | ||
| + | * A <tt>megoldas</tt> függvény belsejében minden olyan parancsot pontosvesszővel ('''<tt>;</tt>''') zárjunk le. | ||
| + | * Aki nem töltötte le az octave-ot, megoldhatja a feladatot otthonról a [[Putty_haszn%C3%A1lata|Putty]]-al, belépve a <tt>leibniz</tt>-re és ott használni az <tt>octave</tt>-ot és [[WinScp_haszn%C3%A1lata|WinScp]]-vel szerkeszteni a beküldendő fájlt. Teszteléshez használhatjuk az <tt>octave</tt>-ot parancssorból így: | ||
borbely@leibniz:~$ <b>octave T9_HF5_borbely.m</b> | borbely@leibniz:~$ <b>octave T9_HF5_borbely.m</b> | ||
A lap 2016. november 13., 12:54-kori változata
Octave házi feladat
Adjunk meg octave-ban egy
x = megoldas(n,c,d)
alakban hívható függvényt, ami megadja egy n-ismeretlenes, homogén lineáris egyenletrendszer egy megoldását. Ez az egyenletrendszer n = 6 esetén a következő alakot ölti:
A*x = b
ahol
b = [0; 0; 0; 0; 0; 0] A = 1 -2 1 0 0 0 1 -2 1 0 0 0 0 1 -2 1 0 0 0 0 1 -2 1 0 0 0 0 1 -2 1 0 0 0 1 -2 1
Az első argumentumban megadott n változótól függjön az A mátrix mérete (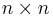 -es) és egyben a jobb oldali vektor mérete is (
-es) és egyben a jobb oldali vektor mérete is (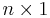 -es)!
-es)!
Az A mátrix rangja n − 2 (tesztelés közben ellenőrizzük), így nulltere 2-dimenziós, tehát az összes megoldás 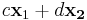 alakba írható, ahol
alakba írható, ahol 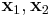 a nullteret kifeszítő vektorok. A függvény tehát az (n,c,d) bemenetre az
a nullteret kifeszítő vektorok. A függvény tehát az (n,c,d) bemenetre az 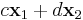 megoldást adja vissza.
megoldást adja vissza.
Segítség:
- Használhatjátok a null vagy rref parancsot!
Formai követelmények:
- A megoldást egy .m kiterjesztésű szövegfájlban küldjétek el.
- A fájl a feladatban kitűzött egyetlen függvény definícióját tartalmazza és semmi mást
- A fájl végén legyen egy üres sor.
- A fájl neve a következő formátumú legyen:
T<tankör>_HF5_<felhasználónév>.m
Beadási határidő: TBD
Tanács:
- A megoldas függvény belsejében minden parancsot pontosvesszővel (;) zárjunk le.
- Érdemes Putty-al belépni a leibniz-re és ott használni az octave-ot és WinScp-vel szerkeszteni a beküldendő fájlt.
- Teszteléshez használhatjuk az octave-ot parancssorból így:
borbely@leibniz:~$ octave T9_HF5_borbely.m
Másik lehetőség
Mielőtt a beadandó házi feladat megoldásához kezdenétek, végezzétek el a következő lépéseket, melyek segítenek a feladat megoldásában!
Adjatok pozitív egész értéket egy változónak, pl.
>> n = 4
Nézzétek meg mi történik a pascal(n) és a pascal(n,-1) parancsok hatására! Állítsatok elő egy $n\times(2n)$ méretű mátrixot, melynek első blokkja egy Pascal-háromszög (alsó háromszögmátrix), mellette egy egységmátrix, azaz például $n=4$ esetén
1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 1 2 1 0 0 0 1 0 1 3 3 1 0 0 0 1
Nevezzétek el e mátrixot P-nek. Ezután képezzetek egy n-dimenziós b vektort, melynek elemei 2-hatvány plusz 1 alakúak 20 + 1-től indulva, például esetünkben
2 3 5 9
Aki kicsit utánaszámol, láthatja, hogy a 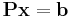 egyenletrendszer megoldható, egy megoldása a csupa 1-esből álló vektor. Határozzátok meg ennek a sortérbe eső egyetlen megoldását (mátrixosztás!). Az összes megoldáshoz meg kell még határozni a nullteret kifeszítő vektorokat. Ezt az octave a
egyenletrendszer megoldható, egy megoldása a csupa 1-esből álló vektor. Határozzátok meg ennek a sortérbe eső egyetlen megoldását (mátrixosztás!). Az összes megoldáshoz meg kell még határozni a nullteret kifeszítő vektorokat. Ezt az octave a
null(P)
paranccsal megadja.
Végül a beadandó feladat: Írjatok egy függvényt, melynek egyetlen paramétere n, és amely válaszul kiírja a fenti egyenletrendszer egyetlen sortérbe eső megoldását és a nullteret generáló vektorok mátrixát abban az esetben, ha n < 8! Ha 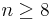 , a program csak annyit írjon ki, hogy "Túl nagy adat!". Például n = 4 esetén
, a program csak annyit írjon ki, hogy "Túl nagy adat!". Például n = 4 esetén
1.3333e+00 1.3333e+00 1.0000e+00 3.3333e-01 6.6667e-01 3.3333e-01 4.4409e-16 3.3333e-01
-0.616696 -0.106047 -0.043625 0.021813 0.399665 -0.409452 -0.144854 -0.010906 -0.165320 0.570204 -0.172812 -0.163594 -0.067442 -0.293872 0.778499 -0.389249 0.616696 0.106047 0.043625 -0.021813 0.217031 0.515499 0.188479 -0.010906 -0.017314 0.354746 0.506146 0.163594 -0.018896 -0.082339 0.218125 0.890937
Formai követelmények:
- A megoldást egy .m kiterjesztésű szövegfájlban küldjétek el. Igyekezzetek a szövegfájlt a program értelme szerint formázni 2 szóközzel beljebb húzva a sorokat (ez nem kötelező). Például így:
function ...
if ...
...
else
...
endif
endfunction
- A fájl a feladatban kitűzött egyetlen függvény definícióját tartalmazza és semmi mást! (pl. ne legyen benne prompt sem, azaz >>)
- A fájl végén legyen egy üres sor.
- A fájl neve a következő formátumú legyen:
T<tankör>_HF5_<felhasználónév>.m
Beadási határidő: TBD
Tanács:
- A megoldas függvény belsejében minden olyan parancsot pontosvesszővel (;) zárjunk le.
- Aki nem töltötte le az octave-ot, megoldhatja a feladatot otthonról a Putty-al, belépve a leibniz-re és ott használni az octave-ot és WinScp-vel szerkeszteni a beküldendő fájlt. Teszteléshez használhatjuk az octave-ot parancssorból így:
borbely@leibniz:~$ octave T9_HF5_borbely.m