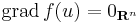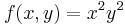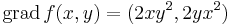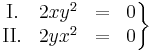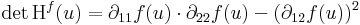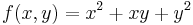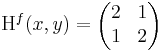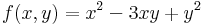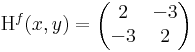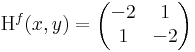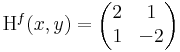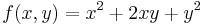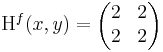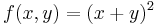|
|
| 1. sor: |
1. sor: |
| − | :''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.''
| + | ==Többváltozós függvény szélsőértéke== |
| − | | + | ===Szélsőérték szükséges feltétele=== |
| − | | + | '''Tétel''' - ''Fermat-tétel'' - Legyen ''f'': '''R'''<sup>n</sup> <math>\supset\!\to</math> '''R''', ''u'' ∈ int Dom(''f''), ''f'' differenciálható ''u''-ban. |
| − | | + | :Ha ''u''-ban ''f''-nek (lokális) szélsőértéke van, akkor |
| − | ==Differenciálhatóság== | + | ::<math>\mathrm{grad}\,f(u)=0_{\mathbf{R}^n}\,</math> |
| − | Legyen ''f'': '''R'''<sup>n</sup> <math>\supset\!\longrightarrow</math> '''R'''<sup>m</sup> és ''u'' ∈ int Dom(f). Azt mondjuk, hogy ''f'' '''differenciálható''' az ''u'' pontban, ha létezik olyan ''A'': '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés, hogy
| + | ''U.is:'' minden ''i''-re az ''i''-edik parciális függvénynek szélsőértéke van ''u''<sub>i</sub>-ben, így az egyváltozós Fermat-tétel miatt ezeknek a deriváltja ''u''<sub>i</sub>-ben 0, így a gradiens értéke 0. |
| − | :<math>\lim\limits_{x\to u}\frac{f(x)-f(u)-\mathcal{A}(x-u)}{||x-u||_{\mathbf{R}^n}}=0_{\mathbf{R}^m}</math>
| + | |
| − | Ekkor ''A'' egyértelmű és az ''f'' leképezés ''u''-bent beli '''deriválttenzor'''ának vagy '''differenciál'''jának nevezzük és d''f''(''u'')-val vagy D''f''(u)-val jelöljük. Ezt a fogalmat néha ''teljes differenciál''nak, ''totális differenciál''nak vagy ''Fréchet-derivált''nak is mondjuk.
| + | |
| − | | + | |
| − | '''Megjegyzés.''' A fenti határérték 0 volta egyenértékű a következő kijelentéssel. Létezik ''A''': ''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés és ε: Dom(''f'') <math>\to</math> '''R'''<sup>m</sup> függvény, melyre:
| + | |
| − | : ε folytonos u-ban és ε(u)=0, továbbá
| + | |
| − | minden ''x'' ∈ Dom(''f'')-re:
| + | |
| − | : <math>f(x)=f(u)+\mathcal{A}(x-u)+\varepsilon(x)||x-u||</math>
| + | |
| − | '''Megjegyzés.''' Azt, hogy ''A'' egyértelmű, a következőkkel bizonyíthatjuk. Legyen ''A'' és ''B'' is a mondott tuljadonságú, azaz létezzenek ε és η az ''u''-ban eltűnő és ott folytonos Dom(''f'')-en értelmezett függvények, melyekre teljesül, hogy minden ''x'' ∈ Dom(''f'')-re
| + | |
| − | :<math>f(x)=f(u)+\mathcal{A}(x-u)+\varepsilon(x)||x-u||</math>
| + | |
| − | :<math>f(x)=f(u)+\mathcal{B}(x-u)+\eta(x)||x-u||</math>
| + | |
| − | ezeket kivonva egymásból és használva '''minden''' ''x''-re:
| + | |
| − | :<math>(\mathcal{A}-\mathcal{B})(x-u)+(\varepsilon(x)-\eta(x))||x-u||=0</math>
| + | |
| − | így minden x = u + ty értékre is az azonosan nullát kapjuk, ha t pozitív szám, y pedig rögzített nemnulla vektor, azaz minden t-re
| + | |
| − | :<math>(\mathcal{A}-\mathcal{B})ty+(\varepsilon(u+ty)-\eta(u+ty))||ty||=0</math>
| + | |
| − | az azonosan 0 függény határértéke t<math>\to</math> 0 esetén szintén nulla:
| + | |
| − | :<math> 0=\lim\limits_{t\to 0}\frac{(\mathcal{A}-\mathcal{B})(ty)+(\varepsilon(u+ty)-\eta(u+ty))||ty||}{t}=(\mathcal{A}-\mathcal{B})y</math>
| + | |
| − | hiszen t-t kiemelhetünk és egyszerűsíthatünk és t<math>\to</math> 0 esetén
| + | |
| − | ε és η nullává válik.
| + | |
| − | Ez viszont pont azt jelenti, hogy a két lineéris operátor a 0 egy környezetében azonosan egyenlő, így ilyen kicsi bázisokon egyenlő, azaz mindenhol egyenlő.
| + | |
| − | ==Jacobi-mátrix==
| + | |
| − | Vizsgáljuk mibe viszi a bázisokat d''f''(''u'') komponensleképezésenként. A d''f''(''u'') lineáris leképezés (<math>e_1</math>,<math>e_2</math>,...,<math>e_n</math>) szetenderd bázisbeli mátrixa legyen: [d''f''(''u'')] = '''A'''. Világos, hogy (d''f''(''u''))(''x'')='''A''' ''x''. Először vegyük az '''A''' első sorvektorát, '''A'''<sub>1</sub>-et és az <math>e_1</math> egységvektor mentén tartunk ''u''-hoz: ''x'' = ''u'' + ''t''<math>e_1</math>. A d''f''(''u'')-t definiáló határértékegyenlőség ekkor a következő alakot ölti:
| + | |
| − | :<math>0=\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)-\mathbf{A}_1\cdot(te_1)}{t}=</math>
| + | |
| − | :::<math>=\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)-t\mathbf{A}_1\cdot(e_1)}{t}=</math>
| + | |
| − | :::<math>=-\mathbf{A}_1\cdot e_1+\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)}{t}</math>
| + | |
| − | azaz
| + | |
| − | :<math>\mathbf{A}_1\cdot e_1=\lim\limits_{t\to 0}\frac{f_1(u+te_1)-f_1(u)}{t}=\partial_1 f_1(u)</math>
| + | |
| − | vagyis ''f'' első koordinátafüggvényének <math>f_1</math>-nek az első változó szerinti parciális deriváltja az ''u'' pontban. A többi mátrixelemet ugyanígy:
| + | |
| − | | + | |
| − | :<math>[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix}
| + | |
| − | \partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\ | + | |
| − | \partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\
| + | |
| − | \vdots & \vdots & \ddots & \vdots \\
| + | |
| − | \partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\
| + | |
| − | \end{bmatrix}</math>
| + | |
| − | amelyet '''Jacobi-mátrix'''nak nevezünk.
| + | |
| − | | + | |
| − | ==A differenciálás tulajdonságai==
| + | |
| − | ===Lineáris és affin függvény deriváltja===
| + | |
| − | Az ''A'' : '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
| + | |
| − | | + | |
| − | ''Ugyanis, '' legyen ''u'' ∈ '''R'''<sup>n</sup>. Ekkor | + | |
| − | | + | |
| − | :<math>\lim\limits_{x\to u}\frac{\mathcal{A}(x)-\mathcal{A}(u)-\mathcal{A}(x-u)}{||x-u||}=\lim\limits_{x\to u}0=0</math>
| + | |
| − | | + | |
| − | c konstans függény esetén az d''c''(''u'') <math>\equiv</math> 0 alkalmas differenciálnak, mert
| + | |
| − | :<math>\lim\limits_{x\to u}\frac{c-c-0\cdot(x-u)}{||x-u||}=\lim\limits_{x\to u}0=0</math>
| + | |
| − | így világos, hogy c + ''A'' alakú affin függvények is differenciálhatóak, és differenciáljuk minden pontban az az ''A'' lineáris leképezés, melynek eltolásából az affin származik. Ezt szintén behelyettesítéssel ellenőrizhetjük. | + | |
| − | | + | |
| − | Tehát minden ''u'' ∈ '''R'''<sup>n</sup>-re
| + | |
| − | :<math>\mathrm{d}\mathcal{A}(u)=\mathcal{A},\quad\quad\mathrm{d}c(u)\equiv 0,\quad\quad\mathrm{d}(b+\mathcal{A}\circ(id-a))(u)=\mathcal{A}</math>
| + | |
| | | | |
| | ====Példa==== | | ====Példa==== |
| | + | :<math>f(x,y)=x^2y^2\,</math> |
| | + | Ennek gradiense: |
| | + | :<math>\mathrm{grad}\,f(x,y)=(2xy^2,2yx^2)</math> |
| | + | Az |
| | + | :<math>\left. |
| | + | \begin{matrix} |
| | + | \mathrm{I.} & 2xy^2 & = & 0\\ |
| | + | \mathrm{II.} & 2yx^2 & = & 0\\ |
| | + | \end{matrix} |
| | + | \right\}</math> |
| | + | egyenletrendszer megoldásai: ''x'' = 0, ''y'' tetszőleges ill. ''y'' = 0 és ''x'' tetszőleges. A szélsőértékek helyei csak ezek közül kerülhetnek ki és ezek valóban szélsőértékek is, mert ezeken a függvény 0-t vesz fel, ami a lehetséges legkisebb értéke. |
| | + | :<gnuplot> |
| | + | set pm3d |
| | + | set size 0.8,0.8 |
| | + | set xrange [-1:1] |
| | + | set yrange [-1:1] |
| | + | set zrange [-2:2] |
| | + | set view 50,30,1,1 |
| | + | unset xtics |
| | + | unset ytics |
| | + | unset ztics |
| | + | unset key |
| | + | unset colorbox |
| | + | splot 5*x*x*y*y |
| | + | </gnuplot> |
| | + | ===Másodikderivált próba=== |
| | + | Kétszer differenciálható függvényre vonatkozóan megfogalmazhatjuk a lokális maximum és minimum létezésének elégséges feltételét. Csak a kétváltozós függvényekkel foglalkozunk. Tegyük fel, hogy grad ''f''(u) = 0 és H<sup>f</sup>(u) az ''f'' Hesse-mátrixa |
| | + | # ha det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') < 0, akkor ''f''-nek ''u''-ban '''maximuma''' van |
| | + | # ha det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') > 0, akkor ''f''-nek ''u''-ban '''minimuma''' van |
| | + | # ha det H<sup>f</sup>(u) < 0, akkor ''f''-nek biztosan nincs szélsőértéke, ún. '''nyeregpont'''ja van |
| | + | # ha det H<sup>f</sup>(u) = 0, akkor a próba nem járt sikerrel, azaz további vizsgálatokat igényel annak eldöntése, hogy ''u'' szélsőérték hely-e. |
| | | | |
| − | Az ''A'': '''x''' <math>\mapsto</math> 2<math>x_1</math> + 3<math>x_2</math> - 4<math>x_3</math> lineáris leképezés differenciálja az '''u''' pontban az '''u'''-tól független
| + | ''Megjegyzések.'' Mivel kétváltozós esetben |
| − | :<math>(\mathrm{d}\mathcal{A}(\mathbf{u}))(x_1,x_2,x_3)=2x_1+3x_2-4x_3\,</math> | + | :<math>\mathrm{det}\,\mathrm{H}^f(u)=\partial_{11}f(u)\cdot \partial_{22}f(u)-(\partial_{12}f(u))^2</math> |
| − | és Jacobi-mátrixa a konstans
| + | ezért olyan eset nem létezik, hogy det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') = 0. |
| − | :<math>\mathbf{J}^\mathcal{A}(\mathbf{u})=\begin{bmatrix}2 & 3 & -4\end{bmatrix}</math>
| + | |
| − | mátrix.
| + | |
| | | | |
| − | Világos, hogy a | + | Világos, hogy a másodikderivált tipikusan azoknál a függvényeknél jár sikerrel, melyeket egy másodfokú függvény közelít a legjobban (aszimptotikusan másodfokúak). Ha a függvény ennél magasabb fokú, akkor a második deriváltak eltűnnek és a Hesse-mártix elfajul (vagy legalább is tipikusan elfajul). |
| − | :<math>\mathrm{pr}_i:(x_1,x_2,...,x_i,...,x_n)\mapsto x_i</math>
| + | |
| − | koordináta vagy projekciófüggvény lineáris, differenciálja minden '''u''' pontban saját maga és ennek mátrixa:
| + | Ha tehát |
| − | :<math>[\mathrm{grad}\,\mathrm{pr_i}]=\mathbf{J}^{\mathrm{pr}_i}(\mathbf{u})=\begin{bmatrix}0 & 0 & ... & 1 & ...& 0\end{bmatrix}</math> | + | :<math>\mathrm{H}^{f}(u)=\begin{pmatrix} |
| − | ahol az 1 az i-edik helyen áll. Másként
| + | A & B \\ |
| − | :<math>\partial_kx_i=\delta_{ki}</math>
| + | B & C |
| − | ahol
| + | \end{pmatrix}</math>, akkor <math>\mathrm{det\,H}^{f}(u)=AC - B^2 </math>, |
| − | :<math>\delta_{ij}=\left\{\begin{matrix}1, \mbox{ ha }i=j\\0, \mbox{ ha }i\ne j \end{matrix}\right.</math>
| + | és így a tipikus példák a következők. |
| − | azaz a Kronecker-féle δ szimbólum.
| + | |
| | | | |
| − | ===Függvények lineáris kombinációja=== | + | ====Példák==== |
| − | Ha ''f'' és ''g'' a ''H'' ⊆ '''R'''<sup>n</sup> halmazon értelmezett '''R'''<sup>m</sup>-be képező, az ''u'' ∈ ''H''-ban differenciálható függvények, akkor minden λ számra
| + | |
| − | :<math>\lambda.f\,</math> is differenciálható ''u''-ban és <math>\mathrm{d}(\lambda.f)(u)=\lambda.\mathrm{d}f(u)\,</math> és
| + | |
| − | :<math>f+g\,</math> is differenciálható ''u''-ban és <math>\mathrm{d}(f+g)(u)=\mathrm{d}f(u)+\mathrm{d}g(u)\,</math>
| + | |
| − | ''Ugyanis,'' a mondott differenciálokkal és a
| + | |
| − | :<math>\varepsilon_{\lambda.f}=\lambda.\varepsilon_{f}\,</math>
| + | |
| − | :<math>\varepsilon_{f+g}=\varepsilon_{f}+\varepsilon_{g}\,</math>
| + | |
| − | választással, ezek az ''u''-ban folytonosak lesznek és a lineáris résszekel együtt ezek előállítják a skalárszoros és összegfüggvények megváltozásait.
| + | |
| − | ===Függvénykompozíció differenciálja===
| + | |
| − | '''Tétel. ''' Legyen ''g'': '''R'''<sup>n</sup> ⊃<math>\to</math> '''R'''<sup>m</sup>, az ''u''-ban differenciálható, ''f'': '''R'''<sup>m</sup> ⊃<math>\to</math> '''R'''<sup>k</sup> a ''g''(''u'')-ban differenciálható függvény, ''u'' ∈ int Dom(''f'' <math>\circ</math> ''g''). Ekkor az
| + | |
| − | :<math>f\circ g</math> differenciálható ''u''-ban és
| + | |
| − | :<math> \mathrm{d}(f\circ g)(u)=\mathrm{d}f(g(u))\circ\mathrm{d}g(u)</math>
| + | |
| | | | |
| − | ''Bizonyítás. '' Alkalmas ε, ''A'' és η ''B'' párral, minden ''x'' ∈ Dom(''f'' <math>\circ</math> ''g'')-re: | + | '''1.''' Ha B kicsi, azaz az AC-hez képest kis abszolútrétékű szám, akkor a szélsőérték irányába mozdul el a feladat. |
| − | :<math>f(g(x))=f(g(u))+\mathcal{A}(g(x)-g(u))+\varepsilon(g(x))||g(x)-g(u)||)=</math>
| + | :<math>f(x,y)=x^2+xy+y^2\,</math> |
| − | ::<math>=f(g(u))+\mathcal{A}(\mathcal{B}(x-u)+\eta(x)||x-u||)+\varepsilon(g(x))||g(x)-g(u)||)=</math>
| + | |
| − | ::<math>=f(g(u))+(\mathcal{A}\circ\mathcal{B})(x-u)+\mathcal{A}(\eta(x)||x-u||)+\varepsilon(g(x))||g(x)-g(u)||)=</math>
| + | |
| − | ::<math>=f(g(u))+(\mathcal{A}\circ\mathcal{B})(x-u)+(\mathcal{A}(\eta(x))+\varepsilon(g(x))||\mathcal{B}\frac{x-u}{||x-u||}+\eta(x)||)||x-u||</math>
| + | |
| − | Innen leolvasható a differenciál és a másodrendben eltűnő mennyiség vektortényezője, az
| + | |
| − | :<math>\varepsilon_{f\circ g}(x)=\mathcal{A}(\eta(x))+\varepsilon(g(x))||\mathcal{B}\frac{x-u}{||x-u||}+\eta(x)||</math> | + | |
| − | melyben az első tag a 0-hoz tart, mivel a lineáris leképezés a 0-ban folytonos, és η a 0-hoz tart az ''u''-ban. A második tag nulla szor korlátos alakú, hiszen a lineáris leképezés Lipschitz-tuladonsága folytán ''B'' minden egységvektoron korlátos értéket vesz fel.
| + | |
| | | | |
| − | Ennek a tételnek a legegyszerűbb, de már vektorokat tartalmazó formáját írja át "fogyasztható" formába az alábbi
| + | Ekkor grad ''f'' = ( 2x + y , 2y + x ) és |
| − | | + | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix} |
| − | '''Következmény.''' Ha ''g'': '''R'''<sup>n</sup> ⊃<math>\to</math> '''R''', az ''u''-ban differenciálható, ''f'': '''R''' ⊃<math>\to</math> '''R''' a ''g''(''u'')-ban differenciálható függvény, ''u'' ∈ int Dom(''f'' <math>\circ</math> ''g''), akkor
| + | 2 & 1 \\ |
| − | :<math>f\circ g</math> differenciálható ''u''-ban és
| + | 1 & 2 |
| − | :<math> \mathrm{grad}(f\circ g)(u)=f'(g(u)).\mathrm{grad}\,g(u)</math> | + | \end{pmatrix}</math> |
| − | Ahol . a skalárral való szorzást jelöli.
| + | azaz 4 - 1 = 3 > 0 és 2 > 0 miatt minimum. |
| − | | + | :<gnuplot> |
| − | ====1. Példa==== | + | set pm3d |
| − | :<math>\Phi(\mathbf{r})=|\mathbf{r}|=\sqrt{\mathbf{r}^2}</math>
| + | set size 0.8,0.8 |
| − | Először a gradienst számítjuk ki. Mivel a gyökfüggvény nem differenciálható a 0-ban, ezért a differenciál csak nemnulla '''r'''-re számítható ki. 0-ban a függvény tényleg nem differenciálható, mert a parciális deriváltak nem léteznek.
| + | set xrange [-1:1] |
| − | :<math>\Phi=\sqrt{.}\circ (.)^2\,</math>
| + | set yrange [-1:1] |
| − | és
| + | set zrange [-2:2] |
| − | :<math>\sqrt{.}\,'=\frac{1}{2\sqrt{.}}</math> illetve <math>\mathrm{grad}\, \mathbf{r}^2=2\mathbf{r}\,</math>
| + | set view 50,30,1,1 |
| − | Ezért
| + | unset xtics |
| − | :<math>\mathrm{grad}\,\Phi(\mathbf{r})=\sqrt{.}'(\mathbf{r}^2). \mathrm{grad}\,\mathbf{r}^2=\frac{1}{2\sqrt{\mathbf{r}^2}}\cdot 2\mathbf{r}=\frac{\mathbf{r}}{|\mathbf{r}|}</math>
| + | unset ytics |
| − | Ha valakinek a differenciál leképezés kell, akkor pedig:
| + | unset ztics |
| − | :<math>\mathrm{d}\sqrt{v}:y\mapsto \frac{1}{2\sqrt{v}}\cdot y </math>
| + | unset key |
| − | :<math>v=\mathbf{r}^2\,</math>
| + | unset colorbox |
| − | :<math>\mathrm{d}\mathbf{r}^2:\mathbf{x}\mapsto 2\mathbf{r}\cdot \mathbf{x}</math> | + | splot x*x+x*y+y*y |
| − | Ezek kompozíciója:
| + | </gnuplot> |
| − | :<math>\mathrm{d}\Phi(\mathbf{r}):\mathbf{x}\mapsto \frac{1}{2\sqrt{\mathbf{r}^2}}.2\mathbf{r}\cdot\mathbf{x}=\frac{\mathbf{r}}{|\mathbf{r}|}\cdot\mathbf{x}</math>
| + | |
| − | Szemléleti okokból lényeges, hogy itt . a skalárral való szorzás, <math>\cdot</math> a skaláris szorzás.
| + | |
| − | | + | |
| − | ====2. Példa====
| + | |
| − | :<math>\Psi(\mathbf{r})=|\mathbf{r}|^{\alpha}</math> | + | |
| − | :<math>\mathrm{d}\Psi(\mathbf{r}):\mathbf{x}\mapsto \alpha|\mathbf{r}|^{\alpha-1}.\frac{\mathbf{r}}{|\mathbf{r}|}\cdot\mathbf{x}</math>
| + | |
| − | illetve a gradiens:
| + | |
| − | :<math>\mathrm{grad}\,|\mathbf{r}|^\alpha=\alpha|\mathbf{r}|^{\alpha-1}.\frac{\mathbf{r}}{|\mathbf{r}|}</math>
| + | |
| − | | + | |
| − | ===Folytonosság mint szükséges feltétel===
| + | |
| − | Ha ''f'' differenciálható ''u''-ban, akkor ott folytonos is, ugyanis minden ''x''-re:
| + | |
| − | :<math>f(x)=f(u)+(\mathrm{d}f(u))(x-u)+\varepsilon(x)||x-u||</math>
| + | |
| − | amely tagjai mind folytonosak ''u''-ban.
| + | |
| − | | + | |
| − | ===Skalárfüggvények szorzata===
| + | |
| − | λ, μ: ''H'' <math>\to</math> '''R''', ahol ''H'' ⊆ '''R'''<sup>n</sup> és az ''u'' ∈ ''H''-ban mindketten differenciálhatók, akkor λμ is és
| + | |
| − | :<math>[\mathrm{d}(\lambda\mu)(u)]_{1j}=\partial_j(\lambda\mu)=\mu\partial_j\lambda+\lambda\partial_j\mu=[\mu(u).\mathrm{grad}\,\lambda(u)+\lambda(u).\mathrm{grad}\,\mu(u)]_{j}</math>
| + | |
| − | azaz
| + | |
| − | :<math>\mathrm{grad}(\lambda\mu)(u)=\mu(u).\mathrm{grad}\,\lambda(u)+\lambda(u).\mathrm{grad}\,\mu(u)</math>
| + | |
| − | ====Példa====
| + | |
| − | Számoljuk ki '''r'''<sup>2</sup> deriváltját a szorzat szabálya szerint.
| + | |
| | | | |
| − | Egyrészt, ha '''r''' ≠ '''0''', akkor
| + | '''2.''' Ha |B| nagy (azaz AC-hez képest nagy), akkor a bizonyosan nemszélsőérték irányába. |
| − | :<math>\mathrm{grad}\,\mathbf{r}^2=\mathrm{grad}\,|\mathbf{r}|\cdot|\mathbf{r}|=2|\mathbf{r}|.\mathrm{grad}|\mathbf{r}|=2|\mathbf{r}|.\frac{\mathbf{r}}{|\mathbf{r}| } =2\mathbf{r}\,</math> | + | :<math>f(x,y)=x^2-3xy+y^2\,</math> |
| | | | |
| − | Másrészt, ha '''r''' = '''0''', akkor
| + | Ekkor grad ''f'' = ( 2x + -3y , 2y + -3x ) és |
| − | :<math> \mathbf{r}^2=0+\mathbf{0}\cdot\mathbf{r}+|\mathbf{r}|\cdot |\mathbf{r}|\,</math> | + | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix} |
| − | minden '''r'''-re fennáll, így grad('''id'''<sup>2</sup>)('''0''') = '''0''' alkalmas az ε('''r''')=|'''r'''|-rel, tehát '''r'''<sup>2</sup> differenciálható 0-ban is.
| + | 2 & -3 \\ |
| | + | -3 & 2 |
| | + | \end{pmatrix}</math> |
| | + | azaz 4 - 9 = -5 < 0 miatt nincs szélsőérték: nyeregpont. |
| | + | :<gnuplot> |
| | + | set pm3d |
| | + | set size 0.8,0.8 |
| | + | set xrange [-1:1] |
| | + | set yrange [-1:1] |
| | + | set zrange [-2:2] |
| | + | set view 50,30,1,1 |
| | + | unset xtics |
| | + | unset ytics |
| | + | unset ztics |
| | + | unset key |
| | + | unset colorbox |
| | + | splot x*x -3*x*y+y*y |
| | + | </gnuplot> |
| | | | |
| − | =='''a''' × ... operátor==
| + | '''3.''' Negatív A és C-re és kis B-re: |
| − | Differenciálható-e és ha igen mi a differenciálja, divergenciája, rotációja a
| + | :<math>f(x,y)=-x^2+xy-y^2\,</math> |
| − | :<math>\mathbf{v}:\mathbf{R}^3\to\mathbf{R}^3;\quad \mathbf{v}(\mathbf{r})=\mathbf{a}\times\mathbf{r}</math> | + | |
| − | leképezésnek, ahol '''a''' előre megadott konstans vektor.
| + | |
| − | ===Megoldás===
| + | |
| − | Az '''a''' × ..., azaz az
| + | |
| − | :<math>\mathbf{a}\times\mathrm{I}\,</math> | + | |
| − | (itt I az identitás leképezés) leképezés lineáris, minthogy a vektoriális szorzás mindkét változójában lineáris ('''v''' ∈ ''Lin''('''R'''<sup>3</sup>;'''R'''<sup>3</sup>)), így differenciálható és differenciálja saját maga: | + | |
| − | :<math>\mathrm{d}(\mathbf{a}\times\mathrm{I})(\mathbf{r})=\mathbf{a}\times\mathrm{I}</math>
| + | |
| − | azaz
| + | |
| − | :<math>(\mathrm{d}(\mathbf{a}\times\mathrm{I})(\mathbf{r}))\mathbf{h}=\mathbf{a}\times\mathbf{h}</math>
| + | |
| − | minden '''h''' és '''r''' ∈ '''R'''<sup>3</sup> vektorra.
| + | |
| | | | |
| − | Jacobi-mátrixa (a sztenderd bázisbeli mátrixa) tetszőleges (x,y,z) pontban:
| + | Ekkor grad ''f'' = ( -2x + 3y , -2y + 3x ) és |
| − | : <math>\mathrm{J}^{\mathbf{a}\times\mathrm{I}}(x,y,z)= | + | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix} |
| − | \begin{bmatrix} | + | -2 & 1 \\ |
| − | \;\,0 & -a_3& \;\;\,a_2\\
| + | 1 & -2 |
| − | \;\;\,a_3 & \;\,0 & -a_1\\
| + | \end{pmatrix}</math> |
| − | -a_2 & \;\;\,a_1& \;\,0\\
| + | azaz 4 - 1 = 3 > 0 és -2 < 0 miatt maximum. |
| − | \end{bmatrix}</math> | + | :<gnuplot> |
| − | Mivel a főátlóbeli elemek mind nullák, ezért ebből rögtön következik, hogy div('''a''' × I)('''r''') = 0.
| + | set pm3d |
| − | :<math>[\mathrm{rot}\,\mathbf{v}]_i=\varepsilon_{ijk}\partial_j\varepsilon_{klm}a_lx_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\partial_j x_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\delta_{jm}=\varepsilon_{ijk}\varepsilon_{klj}a_l=</math> | + | set size 0.8,0.8 |
| − | :<math>=\delta_{kk}\delta_{il}a_l-\delta_{ki}\delta_{lk}a_l=3a_i-a_i=2a_i\,</math>
| + | set xrange [-1:1] |
| − | azaz rot '''v''' ('''r''') = 2'''a'''. Az előbb felhasználtuk a kettős vektoriális szorzatra vonatkozó kifejtési tétel indexes alakját, a
| + | set yrange [-1:1] |
| − | :<math>\varepsilon_{ijk}\varepsilon_{klm}=\delta_{jm}\delta_{li}-\delta_{jl}\delta_{im}\,</math> | + | set zrange [-2:2] |
| − | ami azt mondja, hogy ha az ijk és klm-ben a nem azonos párok jó sorrendben következnek, akkor az epszolon 1-et, ha rossz sorrendben, akkor -1-et ad.
| + | set view 50,30,1,1 |
| | + | unset xtics |
| | + | unset ytics |
| | + | unset ztics |
| | + | unset key |
| | + | unset colorbox |
| | + | splot -x*x +x*y-y*y |
| | + | </gnuplot> |
| | | | |
| | + | '''4.''' Ha A és C előjele ellenkező, akkor rögtön következik, hogy nincs sz.é. |
| | + | :<math>f(x,y)=x^2+xy-y^2\,</math> |
| | | | |
| − | =='''a''' <math>\cdot</math> ... operátor==
| + | Ekkor grad ''f'' = ( 2x + y , -2y + x ) és |
| − | Differenciálható-e és ha igen mi a differenciálja
| + | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix} |
| − | :<math>\Phi:\mathbf{R}^3\to\mathbf{R};\quad \Phi(\mathbf{r})=\mathbf{a}\cdot\mathbf{r}</math> | + | 2 & 1 \\ |
| − | leképezésnek, ahol '''a''' előre megadott konstans vektor.
| + | 1 & -2 |
| − | ===Megoldás===
| + | \end{pmatrix}</math> |
| − | Skalártér lévén Φ gradiensét kell kiszámolnunk. Mivel ez is lineáris leképezés, ezért differenciálható és differenciálja saját maga, azaz a gradiens vektor pont '''a''':
| + | azaz -4 - 1 = -5 < 0 azaz nyeregpont. |
| − | :<math>\mathrm{grad}\,(\mathbf{a}\cdot\mathbf{r})=\mathbf{a}</math>
| + | :<gnuplot> |
| − | Ezt persze indexes deriválással is kiszámítható:
| + | set pm3d |
| − | :<math>[\mathrm{grad}\,\Phi]_i=\partial_ia_kx_k=a_k\partial_ix_k=a_k\delta_{ik}=a_i\,</math>
| + | set size 0.8,0.8 |
| − | ==További példa skalárfüggvényre==
| + | set xrange [-1:1] |
| − | Hatérozzuk meg a Φ
| + | set yrange [-1:1] |
| − | :<math>\Phi:\mathbf{R}^3\to\mathbf{R};\quad \Phi(\mathbf{r})=|\mathbf{i}\times\mathbf{r}|</math> | + | set zrange [-2:2] |
| − | (ahol '''i''' az ''x'' irányú egységvektor, |.| a vektor hossza) függvény szintvonalait, differenciálhatóságát, gradiensét!
| + | set view 50,30,1,1 |
| − | ===Megoldás===
| + | unset xtics |
| − | Érdemes koordinátás írásmódra áttérni, hiszen az '''i''' vektor úgy is a koordinátarendszerhez kapcsolódik. A vektoriális szorzás definíciója miatt
| + | unset ytics |
| − | :<math>\Phi(x,y,z)=\Phi(\mathbf{r})=|\mathbf{r}|\cdot\sin(\mathbf{i},\mathbf{r})_\angle=\sqrt{y^2+z^2}</math> | + | unset ztics |
| − | Tehát azok a pontok vannak azonos szintfelületen, melyeknek az [yz] síkra vett vetületük azonos hosszúságú ('''i''' × '''r''' hossza az '''i'''-re merőleges komponense '''r'''-nek). Az
| + | unset key |
| − | :<math>y^2+z^2=0</math> | + | unset colorbox |
| − | egyenlettel megadott pontokban (másként: ''y'' = 0 & ''z'' = 0 & ''x'' tetszőleges) a függvény nem differenciálható, ugyanis a Φ=0 szintfelület elfajúlt módon csak egy egyenes, az ''x'' tengely, így a gradiens vektor iránya nem egyértelmű. Ezt azzal is igazolhatjuk, ha vesszük ezekben a pontokban például az ''y'' irányú parciális függvényt:
| + | splot x*x +x*y-y*y |
| − | :<math>\Phi(x_0,0+t,0)=\sqrt{t^2}=|t|</math>
| + | </gnuplot> |
| − | azaz az (<math>x_0</math>,0,0) pontokhoz tartozó Φ(<math>x_0</math>, . ,0) parciális függvény nem differenciálható a 0-ban.
| + | |
| | | | |
| − | Máshol a gradiensvektor, a parciális deriváltakat kiszámítva
| + | '''5.''' Atipikus eset, ha AC = B<sup>2</sup>. Ekkor nem jár sikerrel a próba: |
| − | :<math>\mathrm{grad}\,\Phi(x,y,z)=\left(0,\frac{y}{\sqrt{y^2+z^2}}, \frac{z}{\sqrt{y^2+z^2}}\right)</math> | + | :<math>f(x,y)=x^2+2xy+y^2\,</math> |
| − | vagy másként:
| + | |
| − | :<math>\mathrm{grad}\,\Phi(\mathbf{r})=\mathbf{i}\times \frac{\mathbf{i}\times \mathbf{r}}{|\mathbf{i}\times \mathbf{r}|}</math>
| + | |
| | | | |
| − | Megjegyezzük, hogy ehhez még a függvénykompozíció deriválási szabályával is lejuthattunk volna:
| + | Ekkor grad ''f'' = ( 2x + 2y , 2y + 2x ) és |
| − | :<math>\mathrm{grad}\,\Phi(\mathbf{r})=\mathrm{grad}\sqrt{(\mathbf{i}\times\mathbf{r})^2}=\frac{1}{2\sqrt{(\mathbf{i}\times\mathbf{r})^2}}\cdot 2(\mathbf{i}\times\mathbf{r})\times(-\mathbf{i})</math> | + | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix} |
| | + | 2 & 2 \\ |
| | + | 2 & 2 |
| | + | \end{pmatrix}</math> |
| | + | azaz 4 - 4 = 0, azaz határozatlan eset. |
| | + | De tudjuk, hogy |
| | + | :<math>f(x,y)=(x+y)^2\,</math> |
| | + | ami pontosan akkor minimális, ha x = -y, azaz ezeken a helyeken van szélsőérték. |
| | + | :<gnuplot> |
| | + | set pm3d |
| | + | set size 0.8,0.8 |
| | + | set xrange [-1:1] |
| | + | set yrange [-1:1] |
| | + | set zrange [-2:2] |
| | + | set view 50,30,1,1 |
| | + | unset xtics |
| | + | unset ytics |
| | + | unset ztics |
| | + | unset key |
| | + | unset colorbox |
| | + | splot (x+y)*(x+y) |
| | + | </gnuplot> |
| | | | |
| | | | |
Kétszer differenciálható függvényre vonatkozóan megfogalmazhatjuk a lokális maximum és minimum létezésének elégséges feltételét. Csak a kétváltozós függvényekkel foglalkozunk. Tegyük fel, hogy grad f(u) = 0 és Hf(u) az f Hesse-mátrixa
Világos, hogy a másodikderivált tipikusan azoknál a függvényeknél jár sikerrel, melyeket egy másodfokú függvény közelít a legjobban (aszimptotikusan másodfokúak). Ha a függvény ennél magasabb fokú, akkor a második deriváltak eltűnnek és a Hesse-mártix elfajul (vagy legalább is tipikusan elfajul).
ami pontosan akkor minimális, ha x = -y, azaz ezeken a helyeken van szélsőérték.
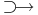R, u ∈ int Dom(f), f differenciálható u-ban.
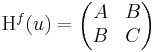, akkor 
,
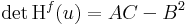