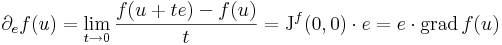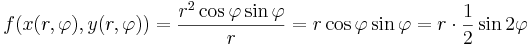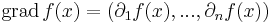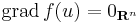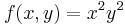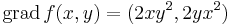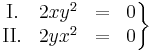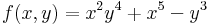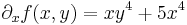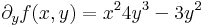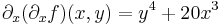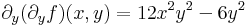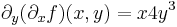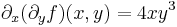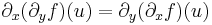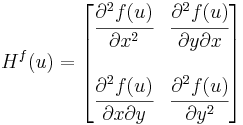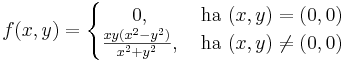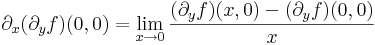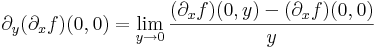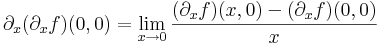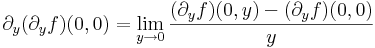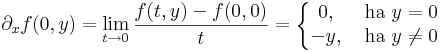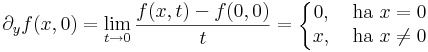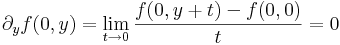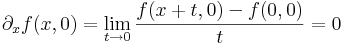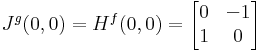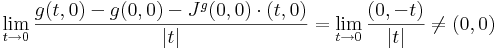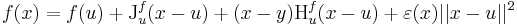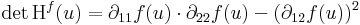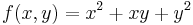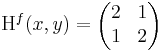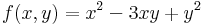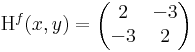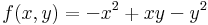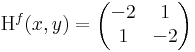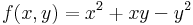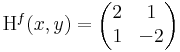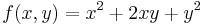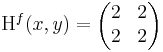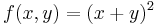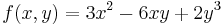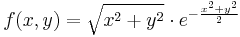Matematika A2a 2008/4. gyakorlat
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
Teljes differenciálhatóság, gyakorlás
1. Hol deriválható?
2. Hol deriválható?
Iránymenti deriválhatóság és differenciálhatóság
Ha e tetszőleges egységvektor, akkor
Példa.
Ekkor
Ha tehát differenciálható, akkor az iránymenti deriváltak (Gateau-deriváltak) is léteznek (e egységvektor):
Ám, polárkoordinátákra áttérve:
φ = π/4-et és π + π/4-et véve a vetületfüggvény a
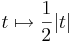 ,
,
ami nem differenciálható a 0-ban.
Illetve nézzük meg a (3,4) vektor mentén!
Megjegyzés. Persze abból, hogy az összes iránymenti derivált létezik, abból nem következik, hogy a függvény totálisan deriválható.
Szélsőérték szükséges feltétele
Egyelőre állapodjunk meg abban, hogy gradiensnek nevezzük a következő többváltozós vektorértékű függvényt: ha f: Rn  R parciálisan differenciálható, akkor
R parciálisan differenciálható, akkor
mely lényegében az f elsőrendű parciális deriváltjaiból képezett vektor.
Később a gradienst egy kissé másképp fogjuk értelmezni és amit most definiáltunk, az a gradiens sztenderd bázisbeli mátrixa lesz (adott pontra vonatkozóan).
Tétel - Fermat-féle szésőértéktétel - Legyen f: Rn  R, u ∈ int Dom(f), f parciálisan differenciálható u-ban.
R, u ∈ int Dom(f), f parciálisan differenciálható u-ban.
- Ha u-ban f-nek (lokális) szélsőértéke van, akkor
U.is: minden i-re az i-edik parciális függvénynek szélsőértéke van ui-ben, így az egyváltozós Fermat-tétel miatt ezeknek a deriváltja ui-ben 0, így a gradiens értéke 0.
Példa
Ennek gradiense:
Az
egyenletrendszer megoldásai: x = 0, y tetszőleges ill. y = 0 és x tetszőleges. A szélsőértékek helyei csak ezek közül kerülhetnek ki és ezek valóban szélsőértékek is, mert ezeken a függvény 0-t vesz fel, ami a lehetséges legkisebb értéke.
Magasabbrendű parciális deriváltak
Ha f parciálisan deriválható, akkor ∂1f és ∂2f szintén kétváltozós függvények (a pontonként a deriváltak, mint függvényértékek értelmezésével) és érdeklődhetünk ezek parciális differenciálhatóságuk iránt. Például:
És valóban:
Tétel. (Young-tétel) Ha a másodrendű parciális deriváltak léteznek az u egy környezetében és folytonosak az u pontban, akkor az u-beli vegyes másodrendű parciláis deriváltak egyenlőek:
Azaz az alábbi, úgy nevezett Hesse-mátrix szimmetrikus:
Feladat. Az a kitétel, hogy az u-ban a másodrenrű parciláis deriváltak folytonosak, nem hagyható el, ugyanis. Legyen
Ekkor a 0-ban nem egyenlő a két vegyes parciális derivált.
Tekintsük a parciális deriváltakat:
Ehhez tehát elegendő kiszámítani a következő föggvényeket: y  (∂xf)(0,y), x
(∂xf)(0,y), x  (∂yf)(x,0). Ehhez a parciális deriváltak:
(∂yf)(x,0). Ehhez a parciális deriváltak:
Megjegyezzük, hogy a g=(∂xf,∂yf) függvény (0,0)-beli parciális deriváltjai nem lehetnek folytonosak, mert ott a függvény nem totálisan diffható. Ugyanis a g Jacobi-mátrixa:
ami a 90˚-os forgatás. Ekkor a g-t a (t,0) vektorral közelítve a 0-ba:
márpedig ha g minden parciális deriváltja folytonos lenne a (0,0)-ban, akkor g totálisan is deriválható lenne.
Többváltozós függvény szélsőértéke
Másodikderivált-próba
Kétszer differenciálható függvényre vonatkozóan megfogalmazhatjuk a lokális maximum és minimum létezésének elégséges feltételét. Csak a kétváltozós függvényekkel foglalkozunk. Tegyük fel, hogy grad f(u) = 0 és Hf(u) az f Hesse-mátrixa
- ha det Hf(u) > 0 és ∂11f(u) < 0, akkor f-nek u-ban maximuma van
- ha det Hf(u) > 0 és ∂11f(u) > 0, akkor f-nek u-ban minimuma van
- ha det Hf(u) < 0, akkor f-nek biztosan nincs szélsőértéke, ún. nyeregpontja van
- ha det Hf(u) = 0, akkor a próba nem járt sikerrel, azaz további vizsgálatokat igényel annak eldöntése, hogy u szélsőérték hely-e.
Megjegyzések. Mivel kétváltozós esetben
ezért olyan eset nem létezik, hogy det Hf(u) > 0 és ∂11f(u) = 0.
Világos, hogy a második derivált tipikusan azoknál a függvényeknél jár sikerrel, melyeket egy másodfokú függvény közelít a legjobban (aszimptotikusan másodfokúak). Ha a függvény ennél magasabb fokú, akkor a második deriváltak eltűnnek és a Hesse-mártix elfajul (vagy legalább is tipikusan elfajul).
Ha tehát
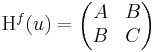 , akkor
, akkor 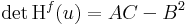 ,
,
és így a tipikus példák a következők.
Példák
1. Ha B kicsi, azaz az AC-hez képest kis abszolútrétékű szám, akkor a szélsőérték irányába mozdul el a feladat.
Ekkor grad f = ( 2x + y , 2y + x ) és
azaz 4 - 1 = 3 > 0 és 2 > 0 miatt minimum.
2. Ha |B| nagy (azaz AC-hez képest nagy), akkor a bizonyosan nemszélsőérték irányába.
Ekkor grad f = ( 2x + -3y , 2y + -3x ) és
azaz 4 - 9 = -5 < 0 miatt nincs szélsőérték: nyeregpont.
3. Negatív A és C-re és kis B-re:
Ekkor grad f = ( -2x + 3y , -2y + 3x ) és
azaz 4 - 1 = 3 > 0 és -2 < 0 miatt maximum.
4. Ha A és C előjele ellenkező, akkor rögtön következik, hogy nincs sz.é.
Ekkor grad f = ( 2x + y , -2y + x ) és
azaz -4 - 1 = -5 < 0 azaz nyeregpont.
5. Atipikus eset, ha AC = B2. Ekkor nem jár sikerrel a próba:
Ekkor grad f = ( 2x + 2y , 2y + 2x ) és
azaz 4 - 4 = 0, azaz határozatlan eset. De tudjuk, hogy
ami pontosan akkor minimális, ha x = -y, azaz ezeken a helyeken van szélsőérték.
6.
7.
| pótló gyakorlat | 5. gyakorlat |
![f(x,y)=\sqrt[3]{x^4+y^4}](/upload/math/2/c/3/2c335aa3afa0bf0f307a9be26d78c087.png)
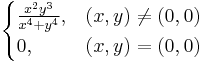
![\lim\limits_{t\to 0}\frac{f(u+te)-f(u)}{t}=\partial_{e}f(u)=[\mathrm{grad}\,f(u)]\cdot e=[\nabla f(u)]\cdot e](/upload/math/6/8/f/68fffe8f513e9e456ec239b3c12e2069.png)
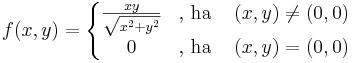
![\mathrm{J}^f(0,0)=[0, 0]\,](/upload/math/5/8/4/5844bda58422be338e9d02beef5b1e3e.png)