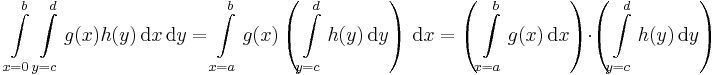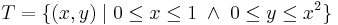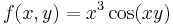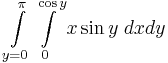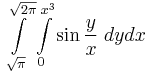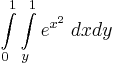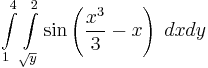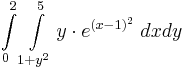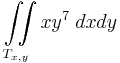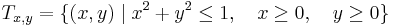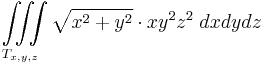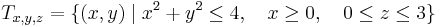Matematika A2a 2008/7. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) |
||
| (egy szerkesztő 27 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
:''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.'' | :''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.'' | ||
| − | + | '''1.''' | |
| − | + | :<math>f(x,y)=xy\sin(x^2y)\,</math> | |
| − | :<math> | + | :''T'' = [0,1]×[0,π/2] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | '''2.''' | |
| + | :<math>f(x,y)=2xy^2e^{x^2y}\,</math> | ||
| + | :''T'' = [0,1]×[0,1] | ||
| + | '''3.''' | ||
| + | :<math>f(x,y)=x^7+\dfrac{\mathrm{arctg}(y)}{1+y^2}\,</math> | ||
| + | :''T'' = [0,1]×[0,1] | ||
| − | ''' | + | '''4.''' |
| + | :T = [-1,1] × [0,π/4] | ||
| + | :<math>f(x,y)=\sin(x^3)\frac{1}{\cos^2 y}</math> | ||
| − | + | '''5.''' | |
| + | :T = [-1,1] × [e,<math>e^2</math>] | ||
| + | :<math>f(x,y)=\sin(x^3)\frac{\sin^{2017}(\mathrm{sh}(y))}{\mathrm{ln}\,y}</math> | ||
| − | + | '''6.''' | |
| − | :<math> | + | :T = [a,b] × [c,d] |
| − | + | :<math>f(x,y)=g(x)h(y)</math> | |
| − | + | ''téglalapon'' szeparálható integrandus integrálja szorzattá esik szét: | |
| − | + | ||
| − | + | :<math>\int\limits_{x=0}^b\int\limits_{y=c}^{d}g(x)h(y)\,\mathrm{d}x\,\mathrm{d}y=\int\limits_{x=a}^b g(x)\left(\int\limits_{y=c}^{d} h(y)\,\mathrm{d}y\right)\,\mathrm{d}x=\left(\int\limits_{x=a}^b g(x)\,\mathrm{d}x\right)\cdot\left(\int\limits_{y=c}^{d} h(y)\,\mathrm{d}y\right)</math> | |
| − | ''' | + | '''7.''' |
| − | : | + | :T = [1,e] × [1,2] |
| − | + | :<math>f(x,y)=\frac{\mathrm{ln}^9\,x}{xy}</math> | |
| − | :<math> | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | '''8.''' | |
| − | :<math> | + | :<math>T=\{(x,y)\mid 0\leq x\leq 1\;\wedge\;0\leq y\leq x^2\}</math> |
| − | + | :<math>f(x,y)=x^3\cos(xy)\,</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | \ | + | |
| − | \ | + | |
| − | \ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | :< | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | '''9.''' | |
| − | + | :<math>\int\limits_{y=0}^\pi\int\limits_{0}^{\cos y}x\sin y\;dxdy</math> | |
| − | + | ||
| − | :<math>\ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | '''10.''' | |
| + | :<math>\int\limits_{\sqrt{\pi}}^{\sqrt{2\pi}}\int\limits_{0}^{x^3}\sin \frac{y}{x}\;dydx</math> | ||
| − | ''' | + | '''11.''' |
| − | :<math> | + | :<math>\int\limits_{0}^{1}\int\limits_{y}^{1}e^{x^2}\;dxdy</math> |
| − | + | '''12.''' | |
| − | :<math>\ | + | :<math>\int\limits_{1}^{4}\int\limits_{\sqrt{y}}^{2}\sin\left(\frac{x^3}{3}-x\right)\;dxdy</math> |
| − | + | ||
| − | + | ||
| − | \ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
| − | ''' | + | '''13.''' |
| − | :<math> | + | :<math>\int\limits_{0}^{2}\int\limits_{1+y^2}^{5}y\cdot e^{(x-1)^2}\;dxdy</math> |
| − | + | '''14.''' | |
| − | :<math>\ | + | :<math>\iint\limits_{T_{x,y}} xy^7\;dxdy</math> |
| − | + | :<math>T_{x,y}=\{(x,y)\mid x^2+y^2\leq 1,\quad x\geq 0, \quad y\geq 0\}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | :< | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
| − | |||
| − | |||
| − | + | '''15.''' | |
| − | :<math>\ | + | :<math>\iiint\limits_{T_{x,y,z}} \sqrt{x^2+y^2}\cdot xy^2 z^2\;dxdydz</math> |
| − | + | :<math>T_{x,y,z}=\{(x,y)\mid x^2+y^2\leq 4,\quad x\geq 0, \quad 0\leq z\leq 3\}</math> | |
| − | + | ||
| − | \ | + | |
| − | + | ||
| − | :< | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | + | <!--Comment |
| − | :<math>f(x,y)=x^2+ | + | |
| + | ==Skalárfüggvények szorzata== | ||
| + | λ, μ: ''H'' <math>\to</math> '''R''', ahol ''H'' ⊆ '''R'''<sup>n</sup> és az ''u'' ∈ ''H''-ban mindketten differenciálhatók, akkor λμ is és | ||
| + | :<math>[\mathrm{d}(\lambda\mu)(u)]_{1j}=\partial_j(\lambda\mu)=\mu\partial_j\lambda+\lambda\partial_j\mu=[\mu(u).\mathrm{grad}\,\lambda(u)+\lambda(u).\mathrm{grad}\,\mu(u)]_{j}</math> | ||
| + | azaz | ||
| + | :<math>\mathrm{grad}(\lambda\mu)(u)=\mu(u).\mathrm{grad}\,\lambda(u)+\lambda(u).\mathrm{grad}\,\mu(u)</math> | ||
| + | ===Példa=== | ||
| + | Számoljuk ki '''r'''<sup>2</sup> deriváltját a szorzat szabálya szerint. | ||
| + | |||
| + | Egyrészt, ha '''r''' ≠ '''0''', akkor | ||
| + | :<math>\mathrm{grad}\,\mathbf{r}^2=\mathrm{grad}\,|\mathbf{r}|\cdot|\mathbf{r}|=2|\mathbf{r}|.\mathrm{grad}|\mathbf{r}|=2|\mathbf{r}|.\frac{\mathbf{r}}{|\mathbf{r}| } =2\mathbf{r}\,</math> | ||
| + | |||
| + | Másrészt, ha '''r''' = '''0''', akkor | ||
| + | :<math> \mathbf{r}^2=0+\mathbf{0}\cdot\mathbf{r}+|\mathbf{r}|\cdot |\mathbf{r}|\,</math> | ||
| + | minden '''r'''-re fennáll, így grad('''id'''<sup>2</sup>)('''0''') = '''0''' alkalmas az ε('''r''')=|'''r'''|-rel, tehát '''r'''<sup>2</sup> differenciálható 0-ban is. | ||
| + | ==Függvénykompozíció differenciálja== | ||
| + | '''Tétel. ''' Legyen ''g'': '''R'''<sup>n</sup> ⊃<math>\to</math> '''R'''<sup>m</sup>, az ''u''-ban differenciálható, ''f'': '''R'''<sup>m</sup> ⊃<math>\to</math> '''R'''<sup>k</sup> a ''g''(''u'')-ban differenciálható függvény, ''u'' ∈ int Dom(''f'' <math>\circ</math> ''g''). Ekkor az | ||
| + | :<math>f\circ g</math> differenciálható ''u''-ban és | ||
| + | :<math> \mathrm{d}(f\circ g)(u)=\mathrm{d}f(g(u))\circ\mathrm{d}g(u)</math> | ||
| + | |||
| + | ''Bizonyítás. '' Alkalmas ε, ''A'' és η ''B'' párral, minden ''x'' ∈ Dom(''f'' <math>\circ</math> ''g'')-re: | ||
| + | :<math>f(g(x))=f(g(u))+\mathcal{A}(g(x)-g(u))+\varepsilon(g(x))||g(x)-g(u)||)=</math> | ||
| + | ::<math>=f(g(u))+\mathcal{A}(\mathcal{B}(x-u)+\eta(x)||x-u||)+\varepsilon(g(x))||g(x)-g(u)||)=</math> | ||
| + | ::<math>=f(g(u))+(\mathcal{A}\circ\mathcal{B})(x-u)+\mathcal{A}(\eta(x)||x-u||)+\varepsilon(g(x))||g(x)-g(u)||)=</math> | ||
| + | ::<math>=f(g(u))+(\mathcal{A}\circ\mathcal{B})(x-u)+(\mathcal{A}(\eta(x))+\varepsilon(g(x))||\mathcal{B}\frac{x-u}{||x-u||}+\eta(x)||)||x-u||</math> | ||
| + | Innen leolvasható a differenciál és a másodrendben eltűnő mennyiség vektortényezője, az | ||
| + | :<math>\varepsilon_{f\circ g}(x)=\mathcal{A}(\eta(x))+\varepsilon(g(x))||\mathcal{B}\frac{x-u}{||x-u||}+\eta(x)||</math> | ||
| + | melyben az első tag a 0-hoz tart, mivel a lineáris leképezés a 0-ban folytonos, és η a 0-hoz tart az ''u''-ban. A második tag nulla szor korlátos alakú, hiszen a lineáris leképezés Lipschitz-tuladonsága folytán ''B'' minden egységvektoron korlátos értéket vesz fel. | ||
| + | |||
| + | Ennek a tételnek a legegyszerűbb, de már vektorokat tartalmazó formáját írja át "fogyasztható" formába az alábbi | ||
| + | |||
| + | '''Következmény.''' Ha ''g'': '''R'''<sup>n</sup> ⊃<math>\to</math> '''R''', az ''u''-ban differenciálható, ''f'': '''R''' ⊃<math>\to</math> '''R''' a ''g''(''u'')-ban differenciálható függvény, ''u'' ∈ int Dom(''f'' <math>\circ</math> ''g''), akkor | ||
| + | :<math>f\circ g</math> differenciálható ''u''-ban és | ||
| + | :<math> \mathrm{grad}(f\circ g)(u)=f'(g(u)).\mathrm{grad}\,g(u)</math> | ||
| + | Ahol . a skalárral való szorzást jelöli. | ||
| + | |||
| + | ''Ugyanis,'' a deriváltak lineáris leképezések: | ||
| + | :<math>v\mapsto (\mathrm{d}g(u))v=(\mathrm{grad}\,(u))\cdot v\,</math> | ||
| + | :<math>w\mapsto (\mathrm{d}f(x))w=f'(x)\cdot w\,</math> | ||
| + | Ezek kompozíciója (f-et az x=g(u)-ban felírva): | ||
| + | :<math>(\mathrm{d}(f\circ g)(u))v=(\mathrm{d}f(g(u)))(\mathrm{d}g(u))v=f'(g(u)).(\mathrm{d}g(u))v=f'(g(u)).(\mathrm{grad}\,g(u))\cdot v\,</math> | ||
| + | |||
| + | Hol diffható? | ||
| + | :<math>\Phi(r)=|r|=\sqrt{r^2}\,</math> | ||
| + | |||
| + | (Útmutatás: abs'=sgn, a 0-án kívül.) | ||
| + | |||
| + | 0-ban nem, mert a parciális deriváltak nem léteznek. Azon kívül: | ||
| + | |||
| + | Külső függvény: | ||
| + | :<math>f(x)=\sqrt(x)\,</math> | ||
| + | nemnulla x-re: | ||
| + | :<math>f'(x)=\frac{1}{2}x^{-\frac{1}{2}}\,</math> | ||
| + | |||
| + | A belső: | ||
| + | :<math>r^2\,</math> | ||
| + | gradiense 2r. | ||
| + | |||
| + | Így: | ||
| + | :<math>\mathrm{grad}\,\sqrt{r^2}=\frac{1}{2}\frac{1}{\sqrt{r^2}}. 2r=\frac{r}{|r|}</math> | ||
| + | |||
| + | |||
| + | ===Gömbszimmetrikus feldatok=== | ||
| + | |||
| + | Mi az | ||
| + | :<math>\Phi(r)=|r|^\alpha\quad\quad\alpha>0</math> | ||
| + | függvény gradiense és differenciálja. Hol diffható? | ||
| + | |||
| + | 0-ban α=1 vagy α<1 esetén biztosan nem diffható, mert a parciális deriváltak nem léteznek. | ||
| + | |||
| + | A külső függvény: | ||
| + | :<math>\,f(x)=x^\alpha</math> | ||
| + | :<math>\,f'(x)=\alpha x^{\alpha-1}</math> | ||
| + | |||
| + | A belső függvény: | ||
| + | <math>\,f(x)=|r|</math> | ||
| + | |||
| + | Ez nem diffható 0-ban (mert a parciális deriváltjai nem léteznek), de máshol: | ||
| + | |||
| + | :<math>\mathrm{grad}\,|r|=\frac{r}{|r|}\,</math> | ||
| + | |||
| + | Ekkor r≠0-ban: | ||
| + | :<math>\mathrm{grad}\,\Phi(r)=\alpha |r|^{\alpha-1}.\frac{r}{|r|}=\alpha r |r|^{\alpha-2}</math> | ||
| + | |||
| + | Ha r=0 és α>1, akkor | ||
| + | :<math>\frac{|r|^\alpha-0-0}{|r|}=|r|^{\alpha-1}\to 0</math> | ||
| + | Tehát a derivált | ||
| + | :<math>\mathrm{grad}\,\Phi(r)=\left\{\begin{matrix}0, &\mathrm{ha} & r=0\\\alpha r |r|^{\alpha-2}, &\mathrm{ha} & r\ne 0\end{matrix}\right.</math> | ||
| + | |||
| + | '''Példa.''' r<sup>3</sup>|r|<sup>α</sup> milyen α-ra diffható mindenhol és mi a deriváltja? | ||
| + | |||
| + | ==Folytonos parciális differenciálhatóság== | ||
| + | |||
| + | Megfordításról a következő esetben beszélhetünk. | ||
| + | |||
| + | '''Tétel.''' Ha az ''f'':'''R'''<sup>n</sup> ⊃<math>\to</math> '''R'''<sup>m</sup> függvény minden parciális deriváltfüggvénye létezik az ''u'' egy környezetében és ''u''-ban a parciális deriváltak folytonosak, akkor ''u''-ban ''f'' differenciálható. (Sőt, folytonosan differenciálható.) | ||
| + | |||
| + | ''Bizonyítás.'' Elegendő az m = 1 esetet vizsgálni. Továbbá a bizonyítás elve nem változik, ha csak az n = 2 esetet tekintjük. Legyen x az u mondott környezetéből vett pont, és x = (<math>x_1</math>,<math>x_2</math>), v=(<math>u_1</math>,<math>x_2</math>), u=(<math>u_1</math>,<math>u_2</math>) Ekkor az [x,v] szakaszon ∂<sub>1</sub>f-hez a Lagrange-féle középértéktétel miatt létezik olyan ξ(<math>x_1</math>)∈[<math>x_1</math>,<math>u_1</math>] szám, és a [v,u] szakaszon ∂<sub>2</sub>f-hez ζ(<math>x_2</math>)∈[<math>x_2</math>,<math>u_2</math>] szám, hogy | ||
| + | :<math>f(x)-f(u)=f(x)-f(v)+f(v)-f(u)=\,</math> | ||
| + | :<math>=\partial_1 f(\xi(x_1),x_2)(x_1-u_1)+\partial_2 f(u_1,\zeta(x_2))(x_2-u_2)=</math> | ||
| + | :<math>=\partial_1f(u)(x_1-u_1)+\partial_2f(u)(x_2-u_2)+</math> | ||
| + | :<math>+(\partial_1 f(\xi(x_1),x_2)-\partial_1f(u))(x_1-u_1)+(\partial_2 f(u_1,\zeta(x_2))-\partial_2f(u))(x_2-u_2)</math> | ||
| + | itt az | ||
| + | :<math>\varepsilon_1(x)=\partial_1 f(\xi(x_1),x_2)-\partial_1f(u)</math> és <math>\varepsilon_2(x)=\partial_2 f(x_1,\zeta(x_2))-\partial_2f(u)</math> | ||
| + | függvények folytonosak ''u''-ban (még ha a ξ, ζ függvények nem is azok), és értékük az ''u''-ban 0. Világos, hogy ez azt jelenti, hogy f differenciálható ''u''-ban. | ||
| + | |||
| + | Világos, hogy a parciális deriváltak folytonossága szükséges a fenti tételben. Az alábbi példában léteznek a parciális deriváltfüggvények az ''u'' egy környzetében, de az ''u''-ban nem folytonosak. | ||
| + | ====Nem differenciálható, nem folytonosan parciálisan differenciálható függvény==== | ||
| + | |||
| + | :<math>f(x,y)=\left\{\begin{matrix}\frac{xy}{\sqrt{x^2+y^2}}& \mbox{, ha }&(x,y)\ne (0,0)\\ | ||
| + | 0&\mbox{, ha }&(x,y)=(0,0)\end{matrix}\right.</math> | ||
| + | parciális deriváltfüggvényei léteznek: | ||
| + | :<math>\frac{\partial f(x,y)}{\partial x}=\frac{y}{\sqrt{x^2+y^2}}-\frac{x^2y}{\sqrt{(x^2+y^2)^3}}</math> | ||
| + | a másik hasonlóan. A 0-ban 0 mindkettő, de az (0,1/n) mentén a 0-ba tartva az 1-hez tart, ami nem 0. | ||
| + | |||
| + | :<math>f(x,y)=\left\{\begin{matrix} | ||
| + | 0,& \mbox{ ha }(x,y)=(0,0)\\ | ||
| + | \frac{xy(x^2-y^2)}{x^2+y^2},& \mbox{ ha }(x,y)\ne(0,0) | ||
| + | \end{matrix}\right.</math> | ||
| + | A Young-tételnél beláttuk, hogy ekkor a 0-ban nem egyenlő a két vegyes parciális derivált. Most már azt is tudjuk miért. A függvény gradiense nem differenciálható totálisan a 0-ban. Ehhez elevenítsük föl, hogy | ||
| + | |||
| + | :<math>J^g(0,0)=H^f(0,0)=\begin{bmatrix} | ||
| + | 0 & -1\\ | ||
| + | 1 & 0 | ||
| + | \end{bmatrix}</math> | ||
| + | ami a 90˚-os forgatás. | ||
| + | |||
| + | Számoljuk ki g értékét a (x,x) alakú pontokban: | ||
| + | |||
| + | :<math>\partial_1f(x,x)=\lim\limits_{t\to 0}\frac{f(x+t,x)-f(0,0)}{t}=\lim\limits_{t\to 0}\frac{(x+t)x((x+t)^2-x^2)}{t((x+t)^2+x^2)}=</math> | ||
| + | :<math>\lim\limits_{t\to 0}\frac{(x+t)x(2tx+t^2)}{t(2x^2+2tx+t^2)}=\lim\limits_{t\to 0}\frac{(x+t)x(2x+t)}{2x^2+2tx+t^2}=\lim\limits_{t\to 0}=x</math> | ||
| + | :<math>\partial_2f(x,x)=\lim\limits_{t\to 0}\frac{f(x,x+t)-f(0,0)}{t}=\lim\limits_{t\to 0}\frac{x(x+t)(x^2-(x+t)^2)}{t(x^2+(x+t)^2)}=</math> | ||
| + | :<math>\lim\limits_{t\to 0}\frac{x(x+t)(-2tx-t^2)}{t(2x^2+2tx+t^2)}=-x</math> | ||
| + | |||
| + | Tehát g(t,t)=(t,-t), és emiatt | ||
| + | |||
| + | :<math>\lim\limits_{t\to 0}\frac{g(t,t)-g(0,0)-J^g(0,0)\cdot (t,t)}{|t|}=\lim\limits_{t\to 0}\frac{(t,-t)-(-t,t)}{|t|}=\lim\limits_{t\to 0}\frac{(2t,-2t)}{|t|}=\lim\limits_{t\to 0}(2\mathrm{sgn}(t),-2\mathrm{sgn}(t))\ne (0,0)\,</math> | ||
| + | márpedig ha g minden parciális deriváltja folytonos lenne a (0,0)-ban, akkor g totálisan is deriválható lenne. | ||
| + | |||
| + | ====Differenciálható, de nem folytonosan parciálisan differenciálható==== | ||
| + | A differenciálhatóság azonban nem elég ahhoz, hogy a parciális deriváltak folytonosak legyenek. | ||
| + | |||
| + | Az | ||
| + | :<math>f(x,y)=\left\{\begin{matrix}(x^2+y^2)\sin\cfrac{1}{x^2+y^2}, & \mbox{ha} & (x,y)\ne (0,0)\\\\ | ||
| + | 0, & \mbox{ha} & (x,y) =(0,0) | ||
| + | \end{matrix}\right. | ||
| + | </math> | ||
| + | differenciálható, hiszen ez az | ||
| + | :<math>f(\mathbf{r})=\left\{\begin{matrix} \mathbf{r}^2\cdot\sin(|\mathbf{r}|^{-2}) & \mbox{ha} & \mathbf{r}\ne \mathbf{0}\\\\ | ||
| + | \mathbf{0}, & \mbox{ha} & \mathbf{r}= \mathbf{0}\end{matrix}\right. | ||
| + | </math> | ||
| + | függvény és '''r''' ≠ '''0'''-ban: | ||
| + | :<math>\mathrm{grad}(f)=\sin(|\mathbf{r}|^{-2}).\mathrm{grad}\,\mathbf{r}^2+\mathbf{r}^2.\mathrm{grad}\,\sin(|\mathbf{r}|^{-2})=</math> | ||
| + | :<math>=\sin(|\mathbf{r}|^{-2}).2\mathbf{r}+\mathbf{r}^2\cdot\cos(|\mathbf{r}|^{-2})\cdot(-2)|\mathbf{r}|^{-3}.\frac{\mathbf{r}}{|\mathbf{r}|}</math> | ||
| + | és grad f nem korlátos. Ez persze a parciális deriváltakon is megátszik: azok sem korlátosak. | ||
| − | + | ===Nevezetes függvénysorozat=== | |
| − | + | * <math>f_n(x,y)=\frac{x^ny}{x^2+y^2}\quad f_n(0,0)=0</math> függvényosztály folytonossága parciális és totális deifferenciálhatósága, folytonos parciális és totális differenciálhatósága | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
| + | --> | ||
A lap jelenlegi, 2017. március 20., 12:58-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
1.
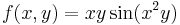
- T = [0,1]×[0,π/2]
2.
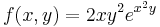
- T = [0,1]×[0,1]
3.
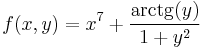
- T = [0,1]×[0,1]
4.
- T = [-1,1] × [0,π/4]
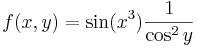
5.
- T = [-1,1] × [e,e2]
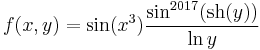
6.
- T = [a,b] × [c,d]
- f(x,y) = g(x)h(y)
téglalapon szeparálható integrandus integrálja szorzattá esik szét:
7.
- T = [1,e] × [1,2]
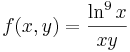
8.
9.
10.
11.
12.
13.
14.
15.
| 6. gyakorlat | 8. gyakorlat |