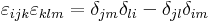Matematika A2a 2008/7. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Megoldás) |
Mozo (vitalap | szerkesztései) (→Megoldás) |
||
| 23. sor: | 23. sor: | ||
:<math>[\mathrm{rot}\,\mathbf{v}]_i=\varepsilon_{ijk}\partial_j\varepsilon_{klm}a_lx_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\partial_j x_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\delta_{jm}=\varepsilon_{ijk}\varepsilon_{klj}a_l=</math> | :<math>[\mathrm{rot}\,\mathbf{v}]_i=\varepsilon_{ijk}\partial_j\varepsilon_{klm}a_lx_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\partial_j x_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\delta_{jm}=\varepsilon_{ijk}\varepsilon_{klj}a_l=</math> | ||
:<math>=\delta_{kk}\delta_{il}a_l-\delta_{ki}\delta_{lk}a_l=3a_i-a_i=2a_i\,</math> | :<math>=\delta_{kk}\delta_{il}a_l-\delta_{ki}\delta_{lk}a_l=3a_i-a_i=2a_i\,</math> | ||
| − | azaz rot '''v''' ('''r''') = 2'''a'''. | + | azaz rot '''v''' ('''r''') = 2'''a'''. Az előbb felhasználtuk a kettős vektoriális szorzatra vonatkozó kifejtési tétel indexes alakját, a |
| + | :<math>\varepsilon_{ijk}\varepsilon_{klm}=\delta_{jm}\delta_{li}-\delta_{jl}\delta_{im}\,</math> | ||
<center> | <center> | ||
A lap 2008. április 4., 20:42-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
a × ... operátor
Differenciálható-e és ha igen mi a differenciálja, divergenciája, rotációja a
leképezésnek, ahol a előre megadott konstans vektor.
Megoldás
Az a × ..., azaz az
(itt I az identitás leképezés) leképezés lineáris, minthogy a vektoriális szorzás mindkét változójában lineáris (v ∈ Lin(R3;R3)), így differenciálható és differenciálja saját maga:
azaz
minden h és r ∈ R3 vektorra.
Jacobi-mátrixa (a sztenderd bázisbeli mátrixa) tetszőleges (x,y,z) pontban:
Mivel a főátlóbeli elemek mind nullák, ezért ebből rögtön következik, hogy div(a × I)(r) = 0.
azaz rot v (r) = 2a. Az előbb felhasználtuk a kettős vektoriális szorzatra vonatkozó kifejtési tétel indexes alakját, a
| 6. gyakorlat | 8. gyakorlat |
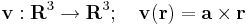
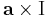
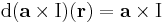
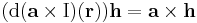
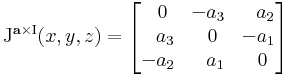
![[\mathrm{rot}\,\mathbf{v}]_i=\varepsilon_{ijk}\partial_j\varepsilon_{klm}a_lx_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\partial_j x_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\delta_{jm}=\varepsilon_{ijk}\varepsilon_{klj}a_l=](/upload/math/6/4/2/642b95a997703a68637ff5897331d591.png)