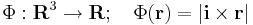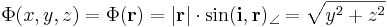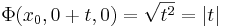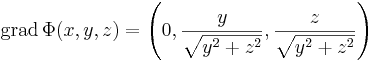Matematika A2a 2008/7. gyakorlat
Mozo (vitalap | szerkesztései) a (→=Megoldás) |
Mozo (vitalap | szerkesztései) (→További példa skalárfüggvényre) |
||
| 41. sor: | 41. sor: | ||
(ahol '''i''' az ''x'' irányú egységvektor, |.| a vektor hossza) függvény szintvonalait, differenciálhatóságát, gradiensét! | (ahol '''i''' az ''x'' irányú egységvektor, |.| a vektor hossza) függvény szintvonalait, differenciálhatóságát, gradiensét! | ||
===Megoldás=== | ===Megoldás=== | ||
| + | Érdemes koordinátás írásmódra áttérni, hiszen az '''i''' vektor úgy is a koordinátarendszerhez kapcsolódik. A vektoriális szorzás definíciója miatt | ||
| + | :<math>\Phi(x,y,z)=\Phi(\mathbf{r})=|\mathbf{r}|\cdot\sin(\mathbf{i},\mathbf{r})_\angle=\sqrt{y^2+z^2}</math> | ||
| + | Tehát azok a pontok vannak azonos szintfelületen, melyeknek az [yz] síkra vett vetületük azonos hosszúságú ('''i''' × '''r''' hossza az '''i'''-re merőleges komponense '''r'''-nek). Az | ||
| + | :<math>y^2+z^2=0</math> | ||
| + | egyenlettel megadott pontokban (másként: ''y'' = 0 & ''z'' = 0 & ''x'' tetszőleges) a függvény nem differenciálható, ugyanis a Φ=0 szintfelület elfajúlt módon csak egy egyenes, az ''x'' tengely, így a gradiens vektor iránya nem egyértelmű. Ezt azzal is igazolhatjuk, ha vesszük ezekben a pontokban például az ''y'' irányú parciális függvényt: | ||
| + | :<math>\Phi(x_0,0+t,0)=\sqrt{t^2}=|t|</math> | ||
| + | azaz az (<math>x_0</math>,0,0) pontokhoz tartozó Φ(<math>x_0</math>, . ,0) parciális függvény nem differenciálható a 0-ban. | ||
| + | Máshol a gradiensvektor, a parciális deriváltakat kiszámítva | ||
| + | :<math>\mathrm{grad}\,\Phi(x,y,z)=\left(0,\frac{y}{\sqrt{y^2+z^2}}, \frac{z}{\sqrt{y^2+z^2}}\right)</math> | ||
| + | vagy másként: | ||
| + | :<math>\mathrm{grad}\,\Phi(\mathbf{r})=\frac{\mathbf{i}\times \mathbf{r}}{|\mathbf{i}\times \mathbf{r}|}\times \mathbf{i}</math> | ||
| − | + | ||
<center> | <center> | ||
{| class="wikitable" style="text-align:center" | {| class="wikitable" style="text-align:center" | ||
A lap 2008. április 5., 08:27-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
a × ... operátor
Differenciálható-e és ha igen mi a differenciálja, divergenciája, rotációja a
leképezésnek, ahol a előre megadott konstans vektor.
Megoldás
Az a × ..., azaz az
(itt I az identitás leképezés) leképezés lineáris, minthogy a vektoriális szorzás mindkét változójában lineáris (v ∈ Lin(R3;R3)), így differenciálható és differenciálja saját maga:
azaz
minden h és r ∈ R3 vektorra.
Jacobi-mátrixa (a sztenderd bázisbeli mátrixa) tetszőleges (x,y,z) pontban:
Mivel a főátlóbeli elemek mind nullák, ezért ebből rögtön következik, hogy div(a × I)(r) = 0.
azaz rot v (r) = 2a. Az előbb felhasználtuk a kettős vektoriális szorzatra vonatkozó kifejtési tétel indexes alakját, a
ami azt mondja, hogy ha az ijk és klm-ben a nem azonos párok jó sorrendben következnek, akkor az epszolon 1-et, ha rossz sorrendben, akkor -1-et ad.
a  ... operátor
... operátor
Differenciálható-e és ha igen mi a differenciálja
leképezésnek, ahol a előre megadott konstans vektor.
Megoldás
Skalártér lévén Φ gradiensét kell kiszámolnunk. Mivel ez is lineáris leképezés, ezért differenciálható és differenciálja saját maga, azaz a gradiens vektor pont a:
Ezt persze indexes deriválással is kiszámítható:
További példa skalárfüggvényre
Hatérozzuk meg a Φ
(ahol i az x irányú egységvektor, |.| a vektor hossza) függvény szintvonalait, differenciálhatóságát, gradiensét!
Megoldás
Érdemes koordinátás írásmódra áttérni, hiszen az i vektor úgy is a koordinátarendszerhez kapcsolódik. A vektoriális szorzás definíciója miatt
Tehát azok a pontok vannak azonos szintfelületen, melyeknek az [yz] síkra vett vetületük azonos hosszúságú (i × r hossza az i-re merőleges komponense r-nek). Az
- y2 + z2 = 0
egyenlettel megadott pontokban (másként: y = 0 & z = 0 & x tetszőleges) a függvény nem differenciálható, ugyanis a Φ=0 szintfelület elfajúlt módon csak egy egyenes, az x tengely, így a gradiens vektor iránya nem egyértelmű. Ezt azzal is igazolhatjuk, ha vesszük ezekben a pontokban például az y irányú parciális függvényt:
azaz az (x0,0,0) pontokhoz tartozó Φ(x0, . ,0) parciális függvény nem differenciálható a 0-ban.
Máshol a gradiensvektor, a parciális deriváltakat kiszámítva
vagy másként:
| 6. gyakorlat | 8. gyakorlat |
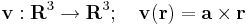
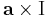
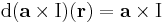
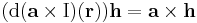
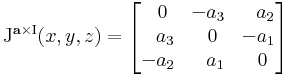
![[\mathrm{rot}\,\mathbf{v}]_i=\varepsilon_{ijk}\partial_j\varepsilon_{klm}a_lx_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\partial_j x_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\delta_{jm}=\varepsilon_{ijk}\varepsilon_{klj}a_l=](/upload/math/6/4/2/642b95a997703a68637ff5897331d591.png)
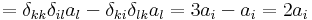
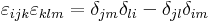
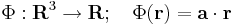
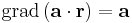
![[\mathrm{grad}\,\Phi]_i=\partial_ia_kx_k=a_k\partial_ix_k=a_k\delta_{ik}=a_i\,](/upload/math/e/6/7/e67c528d00633fe5efe34a67e9c2aef9.png)