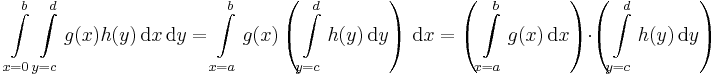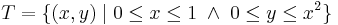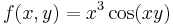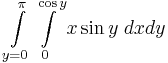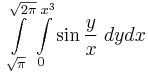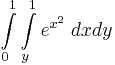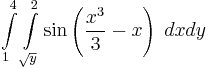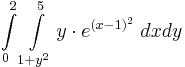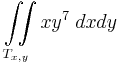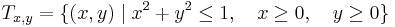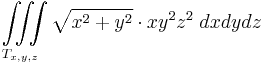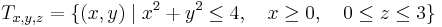Matematika A2a 2008/7. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) |
||
| (egy szerkesztő 11 közbeeső változata nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
:''T'' = [0,1]×[0,1] | :''T'' = [0,1]×[0,1] | ||
'''3.''' | '''3.''' | ||
| − | :<math>f(x,y)=x^7+ | + | :<math>f(x,y)=x^7+\dfrac{\mathrm{arctg}(y)}{1+y^2}\,</math> |
:''T'' = [0,1]×[0,1] | :''T'' = [0,1]×[0,1] | ||
| − | '''4 | + | '''4.''' |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
:T = [-1,1] × [0,π/4] | :T = [-1,1] × [0,π/4] | ||
:<math>f(x,y)=\sin(x^3)\frac{1}{\cos^2 y}</math> | :<math>f(x,y)=\sin(x^3)\frac{1}{\cos^2 y}</math> | ||
| − | ''' | + | '''5.''' |
| − | :T = [-1,1] × [ | + | :T = [-1,1] × [e,<math>e^2</math>] |
| − | :<math>f(x,y)=\sin(x^3)\frac{\sin^{ | + | :<math>f(x,y)=\sin(x^3)\frac{\sin^{2017}(\mathrm{sh}(y))}{\mathrm{ln}\,y}</math> |
| − | ''' | + | '''6.''' |
:T = [a,b] × [c,d] | :T = [a,b] × [c,d] | ||
:<math>f(x,y)=g(x)h(y)</math> | :<math>f(x,y)=g(x)h(y)</math> | ||
| 30. sor: | 26. sor: | ||
:<math>\int\limits_{x=0}^b\int\limits_{y=c}^{d}g(x)h(y)\,\mathrm{d}x\,\mathrm{d}y=\int\limits_{x=a}^b g(x)\left(\int\limits_{y=c}^{d} h(y)\,\mathrm{d}y\right)\,\mathrm{d}x=\left(\int\limits_{x=a}^b g(x)\,\mathrm{d}x\right)\cdot\left(\int\limits_{y=c}^{d} h(y)\,\mathrm{d}y\right)</math> | :<math>\int\limits_{x=0}^b\int\limits_{y=c}^{d}g(x)h(y)\,\mathrm{d}x\,\mathrm{d}y=\int\limits_{x=a}^b g(x)\left(\int\limits_{y=c}^{d} h(y)\,\mathrm{d}y\right)\,\mathrm{d}x=\left(\int\limits_{x=a}^b g(x)\,\mathrm{d}x\right)\cdot\left(\int\limits_{y=c}^{d} h(y)\,\mathrm{d}y\right)</math> | ||
| + | |||
| + | '''7.''' | ||
| + | :T = [1,e] × [1,2] | ||
| + | :<math>f(x,y)=\frac{\mathrm{ln}^9\,x}{xy}</math> | ||
'''8.''' | '''8.''' | ||
:<math>T=\{(x,y)\mid 0\leq x\leq 1\;\wedge\;0\leq y\leq x^2\}</math> | :<math>T=\{(x,y)\mid 0\leq x\leq 1\;\wedge\;0\leq y\leq x^2\}</math> | ||
:<math>f(x,y)=x^3\cos(xy)\,</math> | :<math>f(x,y)=x^3\cos(xy)\,</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''9.''' |
| − | + | :<math>\int\limits_{y=0}^\pi\int\limits_{0}^{\cos y}x\sin y\;dxdy</math> | |
| − | :<math> | + | |
| − | ''' | + | '''10.''' |
| − | + | :<math>\int\limits_{\sqrt{\pi}}^{\sqrt{2\pi}}\int\limits_{0}^{x^3}\sin \frac{y}{x}\;dydx</math> | |
| − | :<math> | + | |
| − | ''' | + | '''11.''' |
| − | + | :<math>\int\limits_{0}^{1}\int\limits_{y}^{1}e^{x^2}\;dxdy</math> | |
| − | :<math> | + | |
| − | + | ||
| − | :<math>\int\limits_{ | + | '''12.''' |
| + | :<math>\int\limits_{1}^{4}\int\limits_{\sqrt{y}}^{2}\sin\left(\frac{x^3}{3}-x\right)\;dxdy</math> | ||
| + | |||
| + | '''13.''' | ||
| + | :<math>\int\limits_{0}^{2}\int\limits_{1+y^2}^{5}y\cdot e^{(x-1)^2}\;dxdy</math> | ||
| + | |||
| + | '''14.''' | ||
| + | :<math>\iint\limits_{T_{x,y}} xy^7\;dxdy</math> | ||
| + | :<math>T_{x,y}=\{(x,y)\mid x^2+y^2\leq 1,\quad x\geq 0, \quad y\geq 0\}</math> | ||
| + | |||
| + | |||
| + | '''15.''' | ||
| + | :<math>\iiint\limits_{T_{x,y,z}} \sqrt{x^2+y^2}\cdot xy^2 z^2\;dxdydz</math> | ||
| + | :<math>T_{x,y,z}=\{(x,y)\mid x^2+y^2\leq 4,\quad x\geq 0, \quad 0\leq z\leq 3\}</math> | ||
| − | |||
| − | |||
| − | |||
A lap jelenlegi, 2017. március 20., 12:58-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
1.
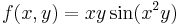
- T = [0,1]×[0,π/2]
2.
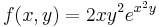
- T = [0,1]×[0,1]
3.
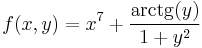
- T = [0,1]×[0,1]
4.
- T = [-1,1] × [0,π/4]
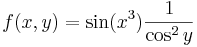
5.
- T = [-1,1] × [e,e2]
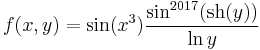
6.
- T = [a,b] × [c,d]
- f(x,y) = g(x)h(y)
téglalapon szeparálható integrandus integrálja szorzattá esik szét:
7.
- T = [1,e] × [1,2]
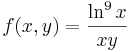
8.
9.
10.
11.
12.
13.
14.
15.
| 6. gyakorlat | 8. gyakorlat |