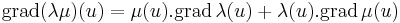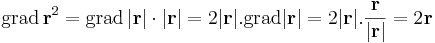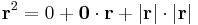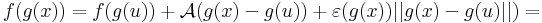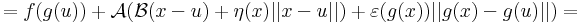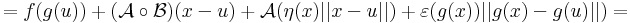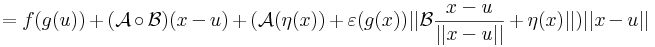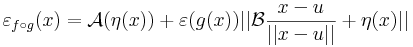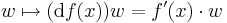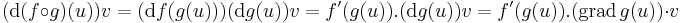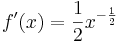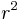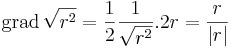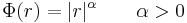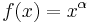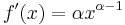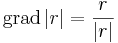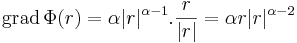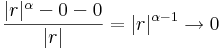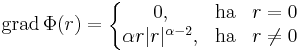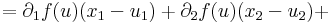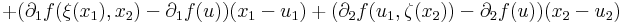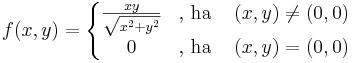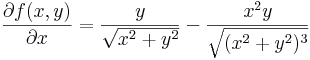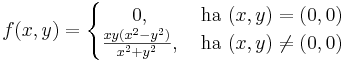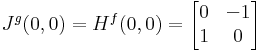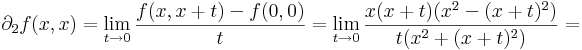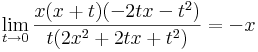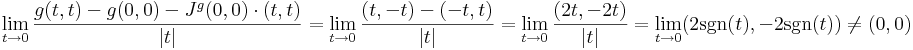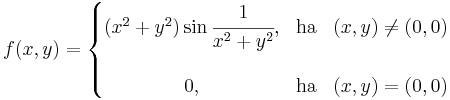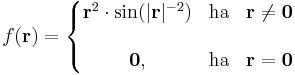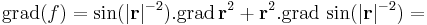|
|
| 159. sor: |
159. sor: |
| | * <math>f_n(x,y)=\frac{x^ny}{x^2+y^2}\quad f_n(0,0)=0</math> függvényosztály folytonossága parciális és totális deifferenciálhatósága, folytonos parciális és totális differenciálhatósága | | * <math>f_n(x,y)=\frac{x^ny}{x^2+y^2}\quad f_n(0,0)=0</math> függvényosztály folytonossága parciális és totális deifferenciálhatósága, folytonos parciális és totális differenciálhatósága |
| | | | |
| − | ==Implicit függvény deriváltja==
| |
| − |
| |
| − | '''Implicit''' megadású '''függvény'''ről akkor beszélünk, amikor egy függvény megadása nem (az explicit módon) ''y'' = ''f''(''x'') alakban történik, hanem az x és y kapcsolatát egy mindkét változót tartalmazó
| |
| − | :<math>F(x,y) = 0 \,</math>
| |
| − | egyenlet írja le.
| |
| − | Például adjunk meg olyan függvényt, melynek grafikonja valamely kör egy szakasza. Az
| |
| − | :<math>x^2+y^2=1\,</math>
| |
| − | egyenletű körből könnyű az ''y'' változót kifejezni, az <math>\mbox{ }_{y=\sqrt{1-x^2}}</math> és <math>\mbox{ }_{y=-\sqrt{1-x^2}}</math> alakokat kapjuk. Bonyolultabb esetekben, például a
| |
| − | :<math>\sin y =x\,</math>
| |
| − | esetén semmi reményünk, hogy az ''y'' változóra valamilyen egyenletrendezéssel általános képletet kapjunk. Az ilyen példák miatt nevezik ezeket a típusú függvényeket ''implicit'', avagy régi, választékos kifejezéssel élve ''bennrekedt'' függvényeknek. A differenciálszámítás szempontjából megelégedhetünk azzal, ha az implicit függvény deriváltját ki tudjuk számolni. Sok esetben ebből már következtethetünk a függvényre vagy annak viselkedésére is.
| |
| − |
| |
| − | A modern analízis szemszögéből egy N × M <math>\rightarrow</math> K normált terek között ható ''F'' függvény ''a'' ∈ ''N'' és ''b'' ∈ ''M'' pontokhoz tartozó implicit függvényén olyan, az ''a'' egy ''U'' környezetén értelmezett és a ''b'' egy ''V'' környezetébe képező ''f'':''U'' <math>\rightarrow </math> ''V'' függvényt értünk, melyre f(a)=b és minden ''x'' ∈ ''U'' pont esetén rendelkezik az
| |
| − | :<math>F(x,f(x))=0\,</math>
| |
| − | tulajdonsággal. Amelyet szavakban úgy fogalmazhatunk meg, hogy az F(x,y)=0 egyenletből az ''y'' változó kifejezhető y=f(x) alakban.
| |
| − |
| |
| − | Most szorítkozzunk csak a kétváltozós esetre és tegyük fel, hogy létezik differenciálható implicit függvénye a differenciálható F függvénynek. Ekkor az F(x,y) függvény implicit függvénye az f(x), ha egy adott (u,v) pontban:
| |
| − | :F(u,v)=0 és
| |
| − | :minden az f értelmezési tartományába eső x-re F(x,f(x))≡0 és
| |
| − | :f(u)=v,
| |
| − | akkor világos, hogy ha
| |
| − | :0 ≡ φ(x) = F(x,f(x)) = (F<math>\circ</math>(id,f))(x) ,
| |
| − | akkor
| |
| − | :φ'(x) ≡ 0
| |
| − | így tehát a függvénykompozíció deriválásának szabálya szerint:
| |
| − | :<math>\varphi'(u)=[\partial_1F(u,v),\partial_2F(u,v)]\cdot \begin{bmatrix}1\\f'(u)\end{bmatrix}=\partial_1 F(u,v)+\partial_2F(u,v)\cdot f'(u)\,=0</math>
| |
| − | így
| |
| − | :<math>f'(u)=-\frac{\partial_1 F(u,v)}{\partial_2 F(u,v)} \,</math>
| |
| − |
| |
| − | ==Implicitfüggvény tétel==
| |
| − |
| |
| − |
| |
| − | '''Tétel''' – ''Implicitfüggvény-tétel '''R'''-beli implicit függvényre'' – Legyen ''F'' az '''R'''<sup>2</sup> egy részhalmazán értelmezett, '''R'''-be képező differenciálható függvény, mely az értelmezési tartománya egy ''(a,b)'' belső pontjában folytonosan differenciálható, F(a,b) = 0 és
| |
| − | :<math>\partial_2 F(a,b)\neq 0</math>
| |
| − | (azaz (a,b)-ben az ''y'' szerinti [[parciális derivált]]ja nem nulla).
| |
| − | Ekkor van a-nak olyan <math>I</math> és b-nek olyan <math>J</math> környezete, hogy F-nek egyértelműen létezik az (a,b) párhoz tartozó f: <math>I</math> <math>\rightarrow</math> <math>J</math> implicit függvénye, mely erősen differenciálható a-ban és deriváltja:
| |
| − | :<math>f'(a)=-\frac{\partial_1 F(a,b)}{\partial_2 F(a,b)}</math>
| |
| − |
| |
| − | ''Vázlatos bizonyítás.'' I. Először megkonstruáljuk az y=y(x) függvényt. Létezik olyan I × J ⊆ Dom(F) az (a,b) körül, hogy ∂<sub>2</sub>F sehol sem nulla, azonos előjelű -- sőt feltehetjük, hogy pozitív. Ez amiatt van, hogy ∂<sub>2</sub>F(a,b) ≠ 0 és ∂<sub>2</sub>F folytonos.
| |
| − |
| |
| − | Az y=y(x) implicit függvény létezése egyenértékű azzal, hogy
| |
| − | :minden ''x'' ∈ <math>I</math>-re az F( x , . ) parciális függvénynek zérushelye van J-ben,
| |
| − | hiszen ekkor minden x-hez létezik olyan ''y'' ∈ J, hogy F(x,y)=0. Belátjuk, hogy minden ilyen x-hez ''egyetlen'' zérushelye van F( x , . )-nek.
| |
| − |
| |
| − | Tekintsük a folytonos F( a , . ) parciális függvényt. A pozitívra választott y-szerinti deriváltból következik, hogy ez <math>I</math>-n szigorúan monoton növekvő. Mivel b-ben zérushelye van ( F(a,b)=0 ), ezért van olyan <math>y_2</math> > b pont, hogy ott F( a , . ) pozitív és <math>y_1</math> < b pont, hogy ott F( a , . ) negatív. Ekkor F folytonossága miatt van az (a,<math>y_1</math>) pontnak olyan környezete, ahol F negatív és
| |
| − | van az (a,<math>y_2</math>) pontnak olyan környezete, ahol F pozitív. Most definiáljuk át <math>I</math>-t és J-t úgy, hogy <math>I</math> × J-n az F egy J-beli elem fölött mindenhol pozitív, egy J-beli elem alatt mindehol negatív értéket vegyen föl.
| |
| − |
| |
| − | A praciális deriváltak folytonosságából az is következik, hogy minden x ∈ <math>I</math>-re az F( x , . ) függvény is szigorúan monoton növekvő, negatív és pozitív értéket is felvevő folytonos függvény, így a [[Bolzano-tétel]] alapján létezik <math>y_x</math> zérushelye és mindegyiknek egyetlen zérushelye létezik.
| |
| − |
| |
| − | II. Állítjuk, hogy a φ:<math>I</math> <math>\rightarrow</math> J, x <math>\mapsto</math> <math>y_x</math> függvény implicit függvénye F-nek, azaz minden x ∈ <math>I</math>-re F(x,φ(x))=0.
| |
| − |
| |
| − | Könnyen belátható, hogy φ folytonos a-ban, hiszen ha a-hoz közeledve mindig találnánk olyan x pontot, hogy φ(x) egy adott ε-nál mindig jobban eltér b-től, akkor φ(x) egy olyan környezetbe esne bele, ahol F mindenhol egy pozitív számnál nagyobb vagy mindenhol egy negatív számnál kisebb. Ám, F(x,φ(x))=0, így ez ellentmondana
| |
| − | F folytonos tulajdonságának.
| |
| − |
| |
| − | III. Végül az implicit függvény differenciálható a-ban, mert ha van (a,b)-ben érintősík, akkor az az érintőegyenesben metszi az [x,y] síkot.
| |
| − |
| |
| − |
| |
| − | === Példák===
| |
| − |
| |
| − | Tekintsük a következő egyenletű síkgörbét:
| |
| − | :<math>x^5+xy+y^5=3\,</math>
| |
| − | Nem lenne könnyű feladat kifejezni belőle y-t, mert az ötödfokú egyenletnek nincs általános megoldóképlete. Mivel a baloldal akárhányszor differenciálható, ezért joggal feltételezhetjük, hogy bizonyos pontokban létezik implicit függvénye. Tegyük fel, hogy φ ilyen függvény. Ekkor az egyenlet
| |
| − | :<math>x^5+x\varphi(x)+(\varphi(x))^5=3</math>
| |
| − | alakú, melynek minden olyan x-nél, ahol φ differenciálható:
| |
| − | :<math>5x^4+\varphi(x)+x\varphi'(x)+5\varphi^4(x)\cdot\varphi'(x)=0</math>
| |
| − | ahonnan a derivált:
| |
| − | <math>\varphi'(x)=-\frac{5x^4+\varphi(x)}{5\varphi^4(x)+x}</math> vagy szimbolikusan: <math>y'=-\frac{5x^4+y}{5y^4+x}</math>.
| |
| − | Alaposabb vizsgálatokkal kideríthető, hogy ez a derivált minden pontban létezik és negatív, így az implicit függvény mindenhol létezik és szigorúan monoton csökkenő. Vegyük észre, hogy a nevezőben lévő kifejezés pont ∂<sub>y</sub>F(x,y) és az implicit függvény létezésének feltétele pont a nevező nullától különböző volta.
| |
| − |
| |
| − | ==Többváltozós eset==
| |
| − |
| |
| − | Ebben az esetben is az „érintősík” végtelenül közelítő tulajdonsága játszik majd fontos szerepet. Jól látható az összefüggés, ha feltesszük, hogy ''F'' egy '''R'''<sup>n</sup>×'''R'''<sup>m</sup>-en értelmezett affin függvény, azaz egy lineáris leképezés eltoltja. Ekkor
| |
| − | :''F(x,y) = F(a+h,b+k) = F(a,b)+dF<sub>1</sub>(a,b)h+dF<sub>2</sub>(a,b)k''.
| |
| − | Amennyiben ''y = y(x)'' olyan, hogy ''y(a) = b'' és ''F(x,y(x)) = 0'', akkor fennáll a ''0 = dF<sub>1</sub>(a,b)h + dF<sub>2</sub>(a,b)k''
| |
| − | egyenlőség és ''k'' kifejezhető, amennyiben az ''A = dF<sub>2</sub>(a,b)'' mátrix invertálható. A ''B = dF<sub>1</sub>(a,b)'' jelöléssel ekkor
| |
| − | :''k = -(A<sup>-1</sup><math>\cdot</math>B) h''.
| |
| − | Általános esetben ez csak egy másodrendűen kicsiny tag hozzávételével lesz igaz, de az implicit függvény létezésének belátásához szükséges a fenti gondolatmenet is.
| |
| − |
| |
| − | [[Banach-tér|Banach-terek]] esetén (melyek akár végtelen [[dimenzió]]sak is lehetnek) a tétel a következő.
| |
| − |
| |
| − | '''Tétel''' – ''Implicitfüggvény-tétel Banach-terekre'' – Legyen E, H, G Banach-terek, F:E × H <math>\rightarrow</math> G olyan függvény, mely (a,b) ∈ E × H-ban erősen differenciálható. Ha a ∂<sub>2</sub>F(a,b) lineáris leképezés injektív és az inverzével együtt folytonos, akkor egyértelműen létezik az F-nek egy az (a,b) párhoz tartozó f lokális implicit függvénye, ez erősen differenciálható a-ban és differenciálja:
| |
| − | : <math>df(a)=-(\partial_2 F(a,b))^{-1}\circ(\partial_1 F(a,b))</math>
| |
| − |
| |
| − | Vagy egy kevésbé absztrakt tétel:
| |
| − |
| |
| − | '''Tétel''' – ''Implicitfüggvény-tétel '''R'''<sup>n</sup>-re'' – Legyen F:'''R'''<sup>n</sup>×'''R'''<sup>m</sup><math>\rightarrow</math>'''R'''<sup>m</sup> folytonosan differenciálható függvény, (a,b) ∈ '''R'''<sup>n</sup>×'''R'''<sup>m</sup>olyanok, hogy F(a,b)=0 és <math>\mbox{ }_{\det\left(\frac{\partial F_i(a,b)}{\partial y_k}\right)_{i,k=1,...,m}\ne 0}</math>. Ekkor egyértelműen létezik F-nek egy az (a,b)-hez tartozó lokális implicit függvénye.
| |
| | | | |
| | | | |
Innen leolvasható a differenciál és a másodrendben eltűnő mennyiség vektortényezője, az
melyben az első tag a 0-hoz tart, mivel a lineáris leképezés a 0-ban folytonos, és η a 0-hoz tart az u-ban. A második tag nulla szor korlátos alakú, hiszen a lineáris leképezés Lipschitz-tuladonsága folytán B minden egységvektoron korlátos értéket vesz fel.
Ennek a tételnek a legegyszerűbb, de már vektorokat tartalmazó formáját írja át "fogyasztható" formába az alábbi
Ahol . a skalárral való szorzást jelöli.
0-ban nem, mert a parciális deriváltak nem léteznek. Azon kívül:
gradiense 2r.
függvény gradiense és differenciálja. Hol diffható?
0-ban α=1 vagy α<1 esetén biztosan nem diffható, mert a parciális deriváltak nem léteznek.
Megfordításról a következő esetben beszélhetünk.
Világos, hogy a parciális deriváltak folytonossága szükséges a fenti tételben. Az alábbi példában léteznek a parciális deriváltfüggvények az u egy környzetében, de az u-ban nem folytonosak.
a másik hasonlóan. A 0-ban 0 mindkettő, de az (0,1/n) mentén a 0-ba tartva az 1-hez tart, ami nem 0.
A Young-tételnél beláttuk, hogy ekkor a 0-ban nem egyenlő a két vegyes parciális derivált. Most már azt is tudjuk miért. A függvény gradiense nem differenciálható totálisan a 0-ban. Ehhez elevenítsük föl, hogy
ami a 90˚-os forgatás.
márpedig ha g minden parciális deriváltja folytonos lenne a (0,0)-ban, akkor g totálisan is deriválható lenne.
A differenciálhatóság azonban nem elég ahhoz, hogy a parciális deriváltak folytonosak legyenek.
és grad f nem korlátos. Ez persze a parciális deriváltakon is megátszik: azok sem korlátosak.
 R, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λμ is és
R, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λμ is és
 Rm, az u-ban differenciálható, f: Rm ⊃
Rm, az u-ban differenciálható, f: Rm ⊃ Rk a g(u)-ban differenciálható függvény, u ∈ int Dom(f
Rk a g(u)-ban differenciálható függvény, u ∈ int Dom(f  g). Ekkor az
g). Ekkor az
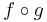 differenciálható u-ban és
differenciálható u-ban és
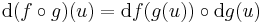
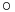 g)-re:
g)-re:
 R, az u-ban differenciálható, f: R ⊃
R, az u-ban differenciálható, f: R ⊃ R a g(u)-ban differenciálható függvény, u ∈ int Dom(f
R a g(u)-ban differenciálható függvény, u ∈ int Dom(f  g), akkor
g), akkor
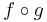 differenciálható u-ban és
differenciálható u-ban és
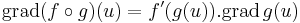
 Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható. (Sőt, folytonosan differenciálható.)
Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható. (Sőt, folytonosan differenciálható.)
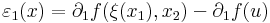 és
és 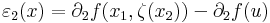
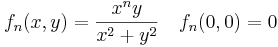 függvényosztály folytonossága parciális és totális deifferenciálhatósága, folytonos parciális és totális differenciálhatósága
függvényosztály folytonossága parciális és totális deifferenciálhatósága, folytonos parciális és totális differenciálhatósága
![[\mathrm{d}(\lambda\mu)(u)]_{1j}=\partial_j(\lambda\mu)=\mu\partial_j\lambda+\lambda\partial_j\mu=[\mu(u).\mathrm{grad}\,\lambda(u)+\lambda(u).\mathrm{grad}\,\mu(u)]_{j}](/upload/math/c/0/6/c06d0e7630e5abf100915f67de31ed5d.png)