Matematika A2a 2008/9. gyakorlat
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Kétváltozós függvény integrálása téglán) |
||
| 20. sor: | 20. sor: | ||
:<math>||\sin(x)||=[\frac{1}{2}x-\frac{1}{2}\sin x]_0^\pi=\frac{\pi}{2}</math> | :<math>||\sin(x)||=[\frac{1}{2}x-\frac{1}{2}\sin x]_0^\pi=\frac{\pi}{2}</math> | ||
:<math>\lambda=\frac{\pi}{\pi^2/4}=\frac{4}{\pi}</math> | :<math>\lambda=\frac{\pi}{\pi^2/4}=\frac{4}{\pi}</math> | ||
| − | == | + | ==Példa téglán történő inegrálásra== |
| − | + | ||
| − | + | ||
| − | + | ||
Ha f(x,y) = x és a [0,2]×[0,2]-n integráljuk, akkor először az y szerinti integrált elvégezve (eközben x állandónak minősül), majd a határozott integrált kiszámolva az x szerintit integrálva: | Ha f(x,y) = x és a [0,2]×[0,2]-n integráljuk, akkor először az y szerinti integrált elvégezve (eközben x állandónak minősül), majd a határozott integrált kiszámolva az x szerintit integrálva: | ||
: <math>\int\limits_{x=0}^2\int\limits_{y=0}^2x\;\mathrm{d}y\mathrm{d}x=\int\limits_{x=0}^2\left(\int\limits_{y=0}^2x\;\mathrm{d}y\right)\mathrm{d}x=</math> | : <math>\int\limits_{x=0}^2\int\limits_{y=0}^2x\;\mathrm{d}y\mathrm{d}x=\int\limits_{x=0}^2\left(\int\limits_{y=0}^2x\;\mathrm{d}y\right)\mathrm{d}x=</math> | ||
| 32. sor: | 29. sor: | ||
: <math>\int\limits_{y=0}^2\int\limits_{x=0}^2x\;\mathrm{d}x\mathrm{d}y=\int\limits_{y=0}^2\left(\int\limits_{x=0}^2x\;\mathrm{d}x\right)\mathrm{d}y=</math> | : <math>\int\limits_{y=0}^2\int\limits_{x=0}^2x\;\mathrm{d}x\mathrm{d}y=\int\limits_{y=0}^2\left(\int\limits_{x=0}^2x\;\mathrm{d}x\right)\mathrm{d}y=</math> | ||
:<math>=\int\limits_{y=0}^2\left[\frac{x^2}{2}\right]_{x=0}^{2} \;\mathrm{d}y=\int\limits_{y=0}^22\;\mathrm{d}y=[2y]_{y=0}^{2}=4</math> | :<math>=\int\limits_{y=0}^2\left[\frac{x^2}{2}\right]_{x=0}^{2} \;\mathrm{d}y=\int\limits_{y=0}^22\;\mathrm{d}y=[2y]_{y=0}^{2}=4</math> | ||
| − | ===2. | + | ==Többváltozós függvény Riemann-integrálja== |
| − | + | ||
| + | A T= J<sub>1</sub>× J<sub>2</sub> korlátos és zárt téglalap egy '''Riemann-felosztás'''án nem mást értünk mint egy olyan kiválasztófüggvényt, mely a T-t unióként előállító, egymásba nem nyúló tengelyekkel márhuzamos oldalú téglalapokból álló halmaz minden egyes eleméhez egy az adott elemben lévő elemet rendel, azaz egy olyan η | ||
| + | függvényt, melyre: | ||
| + | # Dom(η) minden ''I'' eleme tengelyekkel párhuzamos oldalú zárt téglalap, melyek egymásba nem nyúlnak, uniójuk T | ||
| + | # minden ''I'' ∈ Dom(η) esetén <math> \eta(I)\in I</math>. | ||
| + | |||
| + | A T összes '''Riemann-felosztásai halmazát''' RF(T) jelöli. Azon Riemann-felbontások halmazát, amelyekben az összes elem területe (oldalhosszainak szorzata) kisebb egy δ > 0 pozitív számnál, RF<sub>δ</sub>(T) jelöli, ezt a halmazt a T összes '''δ-nál finomabb Riemann-felosztásának''' nevezük. | ||
| + | |||
| + | Egy ''f'', az T-n értelmezett és '''R'''-be képező függvény egy η felosztáshoz tartozó '''Riemann-közelítő összegén''' a | ||
| + | :<math>\sigma_f(\eta)=\sum\limits_{I\in\mathrm{Dom}(\eta)}f(\eta(I)\cdot|I|)</math> | ||
| + | |||
| + | Ekkor már definiálhatjuk az Riemann-integrálhatóságot: | ||
| + | |||
| + | '''Definíció.''' Legyen ''f'':T <math>\to</math> '''R'''egy zárt és korlátos téglán értelmezett függvény. Azt mondjuk, hogy ''f'' '''Riemann-integrálható''' és integrálja az A valós szám, ha | ||
| + | :<math>(\forall \varepsilon> 0)(\exists \delta >0)(\forall \eta\in\mathrm{RF}_{\delta}(T))(|\sigma_f(\eta)-A|< \varepsilon)</math> | ||
| + | |||
| + | Belátható, hogy ha ''f'' integrálható, akkor A egyértelmű és ekkor ennek a számnak a jelölésére az | ||
| + | :<math>\int\limits_{T} f</math>, vagy az <math>\int \limits_{T_{x,y}}f(x,y)\,\mathrm{d}x\mathrm{d}y</math> | ||
| + | szimbólum szolgál. | ||
| + | |||
| + | A T téglalapon Riemann-integrálható függvények halmazát R(T) jelöli. | ||
| + | |||
| + | Az integrál lényegében a függvény grafikonja alatti térfogat. Integrálható függvény esetén létezik ez a térfogat, azaz a Riemann-felosztást egyre finomabbra véve, a Riemann-közelítő összeg minden előre megadott legnagyobb ε eltérésnél közelebb kerül A-hoz. | ||
| + | |||
| + | Világos, hogy ha egy függvény integrálható, akkor minden résztégláján is integrálható (hisz ekkor azokat a felosztásokat kell venni, amik a részintervallumon belül is felosztások, és persze ezek szerint is képezve a határátmenetet, létező határértéket kapunk). | ||
| + | |||
| + | Egy kompakt K halmazon értelmezett f függvény integrálja nem más, mint tetszőleges a K-t tartalmazó T tégla esetén az | ||
| + | :<math>\hat{f}=\left\{\begin{matrix} 0,& \mathrm{ha} & x\in T\setminus K \\f(x),& \mathrm{ha} & x\in K | ||
| + | \end{matrix}\right.</math> | ||
| + | függvény integrálja T-n, ha ez létezik. | ||
| + | |||
| + | ===A Riemann-inregrálhatóság szükséges és elégséges feltétele=== | ||
| + | |||
| + | Bár a Riemann-integrálhatóság általában könnyen kezelhető fogalom, a következő tétel bizonyításához azonban a klasszikus analízis szinte összes eszközét be kell vetni. Nem csoda, hogy csak 1905-ben fogalmazhatta meg Lebesgue, egy tágabb perspektívából szemlélve a Riemann-integrált. | ||
| + | |||
| + | '''Tétel.''' Legyen ''f'': T <math>\to</math> '''R''' korlátos és zárt téglán értelmezett függvény. ''f'' pontosan akkor Riemann-integrálható, ha korlátos, és szakadási helyeinek halmaza Lebesgue-nullmértékű halmaz, azaz | ||
| + | :<math>f\in \mathrm{R}(T)\;\Leftrightarrow\;(f\in \mathrm{B}(T)\;\wedge\; \mathrm{m}(\mathrm{discon}(f))=0)</math> | ||
| + | |||
| + | Itt Lebesgue-nullmértékűnek nevezünk egy ''H'' ⊆ '''R'''<sup>N</sup> halmazt, ha minden ε > 0-hoz létezik olyan (I<sub>n</sub>) téglasorozat, hogy ennek össztérfogata < ε és lefedi ''H''-t. | ||
| + | |||
| + | Biztos nem nullmértékű például egy nemelfajuló intervallum, mert annak a mértéke az intervallum nemnulla hossza. De véges halmaz nullmértékű, mert lefedhető, egy határértékben eltűnő intervallumsorozat-rendszerrel. Belátható, hogy megszámlálható pont nullmértékű halmazt alkot. Konkrétan, könyen belátható, hogy az 1/n pontjai nullmértékű halmazt alkotnak. | ||
| + | |||
| + | Világos, hogy a Dirichlet-függvényes példa azért jó ellenpélda, mert ez a függvény [0,1]-en mindenhol szakad, azaz discon(Dir)=[0,1], melynek a mértéke 1. | ||
| + | |||
| + | '''Példa.''' Felvetődik a kérdés: van-e konitinuum sok helyen szakadó, Riemann-integrálható függvény. A válasz igenlő. (Lásd: az '''ördög lépcsője''' függvényt) | ||
| + | |||
| + | ===A Riemann-integrálhatóság néhány kritériuma=== | ||
| + | |||
| + | Részletezünk néhány hasznos esetet a fenti tételből. | ||
| + | |||
| + | # <math>f\in \mathrm{R}(T)\;\Rightarrow\;f\in \mathrm{B}(T)</math> | ||
| + | #: csak korlátos függvények R-intgrálhatóak | ||
| + | # <math>f\in \mathrm{R}(T)\;\Leftarrow\;f\in \mathrm{C}(T)</math> | ||
| + | #: (Cauchy) világos: ha folytonos, akkor nincs szakadási pontja, és korlátos a Weierstrass-tétel miatt | ||
| + | # <math>f\in \mathrm{R}(T)\;\Leftarrow\;f\in \mathrm{M}[a,b]</math> | ||
| + | ===Kétváltozós függvény integráljának kiszámítása, paraméteres integrál integrálása=== | ||
| + | |||
| + | Legyen f:[a,b]×[c,d]<math> \to</math> '''R''' folytonos. Ekkor az | ||
| + | |||
| + | :<math>F(y)=\int\limits_{x=a}^b f(x,y)\,\mathrm{d}x,\,\quad y\in[c,d]</math> | ||
| + | létezik mert az integrandusa folytonos. Mi több, maga is folytonos. | ||
| + | |||
| + | ''Ugyanis,'' | ||
| + | :<math>F(y)-F(y_0)=\int\limits_{x=a}^b f(x,y)- f(x,y_0)\,\mathrm{d}x\,</math> | ||
| + | Legyen ε > 0 tetszőleges. Mivel f egyenletesen folytonos, ezért létezik δ>0, hogy ha |(x,y)-(x,y<sub>0</sub>)| < δ, akkor | ||
| + | :<math>|f(x,y)- f(x,y_0)|<\frac{\varepsilon}{b-a}\,</math> | ||
| + | Ekkor viszont | ||
| + | :<math>|F(y)-F(y_0)|\leq\int\limits_{x=a}^b |f(x,y)- f(x,y_0)|\,\mathrm{d}x\,\leq\frac{\varepsilon}{b-a}\cdot (b-a)=\varepsilon</math> | ||
| + | Tehát F(y) folytonos (egyenletesen) és így integrélható egyváltozós függvény, azaz létezik: | ||
| + | :<math>A=\int\limits_{y=c}^d\left(\int\limits_{x=a}^b f(x,y)\,\mathrm{d}x\right)\,\mathrm{d}y</math> | ||
| + | |||
| + | Ez alapot ad az integrál kiszámítására: az f(x,y) kétváltozós függvény intergálja tengelyekkel párhuzamos oldalú téglalap alakú tartományon nem függ az integrálás sorrendjétől. Ezesetben a "másik változót" mindig konstansnak vesszük: | ||
| + | :<math>\int\limits_{[a,b]\times[c,d]}f=\int\limits_{x=a}^b\left(\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\right)\mathrm{d}x=\int\limits_{x=a}^b\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\mathrm{d}x=\int\limits_{y=c}^d\left(\int\limits_{x=a}^b f(x,y)\;\mathrm{d}x\right)\mathrm{d}y</math> | ||
A lap 2009. április 23., 21:06-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
Függvénytérbeli projekció
Tekintsük
Ebben a belső szorzat:
Számítsuk ki az
függvény
altérre eső merőleges vetületét!
Kell: λ, hogy f(x) vetülete = λ.sin(x). Projekciótétellel:
Megj: pont ezt adná a Gram-Schmidt is.
Példa téglán történő inegrálásra
Ha f(x,y) = x és a [0,2]×[0,2]-n integráljuk, akkor először az y szerinti integrált elvégezve (eközben x állandónak minősül), majd a határozott integrált kiszámolva az x szerintit integrálva:
Hangsúlyozzuk, hogy itt két esetben a Newton-Leibniz-formulát használtuk a határozott integrál kiszámítására:
ahol F az f primitív függvénye (vagy határozatlan integrálja). Az eslő esetben az y változó szerepeltetése az integrál kiszámítását követően indokolatlanná vált, de az x megmaradt, amit tovább kellet integrálni az x változóra vonatkozóan. Fordított esetben szintén 4-et kapunk:
Többváltozós függvény Riemann-integrálja
A T= J1× J2 korlátos és zárt téglalap egy Riemann-felosztásán nem mást értünk mint egy olyan kiválasztófüggvényt, mely a T-t unióként előállító, egymásba nem nyúló tengelyekkel márhuzamos oldalú téglalapokból álló halmaz minden egyes eleméhez egy az adott elemben lévő elemet rendel, azaz egy olyan η függvényt, melyre:
- Dom(η) minden I eleme tengelyekkel párhuzamos oldalú zárt téglalap, melyek egymásba nem nyúlnak, uniójuk T
- minden I ∈ Dom(η) esetén
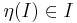 .
.
A T összes Riemann-felosztásai halmazát RF(T) jelöli. Azon Riemann-felbontások halmazát, amelyekben az összes elem területe (oldalhosszainak szorzata) kisebb egy δ > 0 pozitív számnál, RFδ(T) jelöli, ezt a halmazt a T összes δ-nál finomabb Riemann-felosztásának nevezük.
Egy f, az T-n értelmezett és R-be képező függvény egy η felosztáshoz tartozó Riemann-közelítő összegén a
Ekkor már definiálhatjuk az Riemann-integrálhatóságot:
Definíció. Legyen f:T  Regy zárt és korlátos téglán értelmezett függvény. Azt mondjuk, hogy f Riemann-integrálható és integrálja az A valós szám, ha
Regy zárt és korlátos téglán értelmezett függvény. Azt mondjuk, hogy f Riemann-integrálható és integrálja az A valós szám, ha
Belátható, hogy ha f integrálható, akkor A egyértelmű és ekkor ennek a számnak a jelölésére az
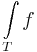 , vagy az
, vagy az 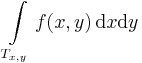
szimbólum szolgál.
A T téglalapon Riemann-integrálható függvények halmazát R(T) jelöli.
Az integrál lényegében a függvény grafikonja alatti térfogat. Integrálható függvény esetén létezik ez a térfogat, azaz a Riemann-felosztást egyre finomabbra véve, a Riemann-közelítő összeg minden előre megadott legnagyobb ε eltérésnél közelebb kerül A-hoz.
Világos, hogy ha egy függvény integrálható, akkor minden résztégláján is integrálható (hisz ekkor azokat a felosztásokat kell venni, amik a részintervallumon belül is felosztások, és persze ezek szerint is képezve a határátmenetet, létező határértéket kapunk).
Egy kompakt K halmazon értelmezett f függvény integrálja nem más, mint tetszőleges a K-t tartalmazó T tégla esetén az
függvény integrálja T-n, ha ez létezik.
A Riemann-inregrálhatóság szükséges és elégséges feltétele
Bár a Riemann-integrálhatóság általában könnyen kezelhető fogalom, a következő tétel bizonyításához azonban a klasszikus analízis szinte összes eszközét be kell vetni. Nem csoda, hogy csak 1905-ben fogalmazhatta meg Lebesgue, egy tágabb perspektívából szemlélve a Riemann-integrált.
Tétel. Legyen f: T  R korlátos és zárt téglán értelmezett függvény. f pontosan akkor Riemann-integrálható, ha korlátos, és szakadási helyeinek halmaza Lebesgue-nullmértékű halmaz, azaz
R korlátos és zárt téglán értelmezett függvény. f pontosan akkor Riemann-integrálható, ha korlátos, és szakadási helyeinek halmaza Lebesgue-nullmértékű halmaz, azaz
Itt Lebesgue-nullmértékűnek nevezünk egy H ⊆ RN halmazt, ha minden ε > 0-hoz létezik olyan (In) téglasorozat, hogy ennek össztérfogata < ε és lefedi H-t.
Biztos nem nullmértékű például egy nemelfajuló intervallum, mert annak a mértéke az intervallum nemnulla hossza. De véges halmaz nullmértékű, mert lefedhető, egy határértékben eltűnő intervallumsorozat-rendszerrel. Belátható, hogy megszámlálható pont nullmértékű halmazt alkot. Konkrétan, könyen belátható, hogy az 1/n pontjai nullmértékű halmazt alkotnak.
Világos, hogy a Dirichlet-függvényes példa azért jó ellenpélda, mert ez a függvény [0,1]-en mindenhol szakad, azaz discon(Dir)=[0,1], melynek a mértéke 1.
Példa. Felvetődik a kérdés: van-e konitinuum sok helyen szakadó, Riemann-integrálható függvény. A válasz igenlő. (Lásd: az ördög lépcsője függvényt)
A Riemann-integrálhatóság néhány kritériuma
Részletezünk néhány hasznos esetet a fenti tételből.
-
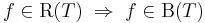
- csak korlátos függvények R-intgrálhatóak
-
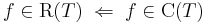
- (Cauchy) világos: ha folytonos, akkor nincs szakadási pontja, és korlátos a Weierstrass-tétel miatt
-
![f\in \mathrm{R}(T)\;\Leftarrow\;f\in \mathrm{M}[a,b]](/upload/math/c/9/0/c902a3acabe9826b0bfdc43482e7dbc2.png)
Kétváltozós függvény integráljának kiszámítása, paraméteres integrál integrálása
Legyen f:[a,b]×[c,d] R folytonos. Ekkor az
R folytonos. Ekkor az
létezik mert az integrandusa folytonos. Mi több, maga is folytonos.
Ugyanis,
Legyen ε > 0 tetszőleges. Mivel f egyenletesen folytonos, ezért létezik δ>0, hogy ha |(x,y)-(x,y0)| < δ, akkor
Ekkor viszont
Tehát F(y) folytonos (egyenletesen) és így integrélható egyváltozós függvény, azaz létezik:
Ez alapot ad az integrál kiszámítására: az f(x,y) kétváltozós függvény intergálja tengelyekkel párhuzamos oldalú téglalap alakú tartományon nem függ az integrálás sorrendjétől. Ezesetben a "másik változót" mindig konstansnak vesszük:
| 8. gyakorlat | 10. gyakorlat |
![L^2[0,\pi]=\{f:[0,\pi]\to \mathbf{R}\mid ''f\quad\mathrm{Lebesgue\mbox{-}int.\mbox{-}hato\!'\,}''\}](/upload/math/f/6/c/f6c6c082f00f7589b656d593157db9bd.png)
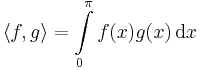
![f(x)=x,\quad x\in[0,\pi]\,](/upload/math/6/6/9/669cfa9c0ae10637390cc81f5b9b8b3d.png)
![L=\mathrm{Span}(\sin)\subseteq L^2[0,\pi]](/upload/math/f/8/0/f806d92c59a1a82a9023b27d6e1fdea0.png)
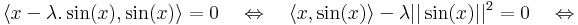
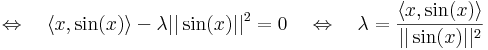
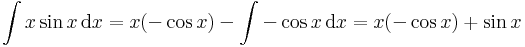
![\int\limits_{0}^\pi x\sin x\,\mathrm{d}x=[x(-\cos x)+\sin x]^\pi_0=\pi](/upload/math/2/a/0/2a0273844dc6505603a239f41f64f6f7.png)
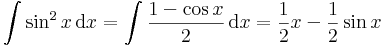
![||\sin(x)||=[\frac{1}{2}x-\frac{1}{2}\sin x]_0^\pi=\frac{\pi}{2}](/upload/math/d/0/6/d067b34159f2cf7d0cd1698c9ebd0ad4.png)
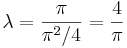
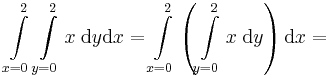
![=\int\limits_{x=0}^2[xy]_{y=0}^{2}\mathrm{d}x=\int\limits_{x=0}^2 2x\;\mathrm{d}x=[x^2]_{x=0}^{2}=4](/upload/math/4/d/7/4d76d92326d729d8a5d68cc30b7ab6c6.png)
![\int\limits_{a}^b f(x)\mathrm{d}x=[F(x)]_{a}^{b}=F(b)-F(a)](/upload/math/8/5/3/853da39029315b2aba44dce65c638884.png)
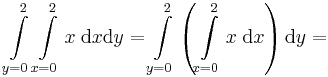
![=\int\limits_{y=0}^2\left[\frac{x^2}{2}\right]_{x=0}^{2} \;\mathrm{d}y=\int\limits_{y=0}^22\;\mathrm{d}y=[2y]_{y=0}^{2}=4](/upload/math/1/a/c/1ac20b7ea17e50cca88da80de185aa12.png)
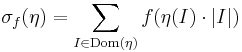
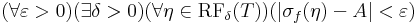
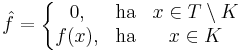
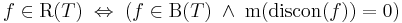
![F(y)=\int\limits_{x=a}^b f(x,y)\,\mathrm{d}x,\,\quad y\in[c,d]](/upload/math/1/2/b/12b448a172a56b9497ea39c986a921de.png)
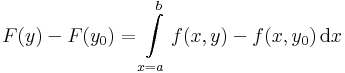
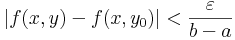
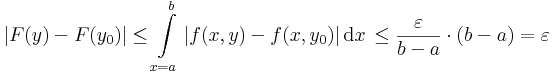
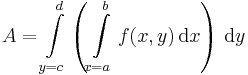
![\int\limits_{[a,b]\times[c,d]}f=\int\limits_{x=a}^b\left(\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\right)\mathrm{d}x=\int\limits_{x=a}^b\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\mathrm{d}x=\int\limits_{y=c}^d\left(\int\limits_{x=a}^b f(x,y)\;\mathrm{d}x\right)\mathrm{d}y](/upload/math/e/f/1/ef10affe1fac157d5fb4427a3a83163c.png)