Matematika A2a 2008/9. gyakorlat
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
Függvénytérbeli projekció
Tekintsük
Ebben a belső szorzat:
Számítsuk ki az
függvény
altérre eső merőleges vetületét!
Kell: λ, hogy f(x) vetülete = λ.sin(x). Projekciótétellel:
Megj: pont ezt adná a Gram-Schmidt is.
Kétváltozós függvény integrálása téglán
Az f(x,y) kétváltozós függvény intergálja tengelyekkel párhuzamos oldalú téglalap alakú tartományon nem függ az integrálás sorrendjétől. Ezesetben a "másik változót" mindig konstansnak vesszük:
1. Példa
Ha f(x,y) = x és a [0,2]×[0,2]-n integráljuk, akkor először az y szerinti integrált elvégezve (eközben x állandónak minősül), majd a határozott integrált kiszámolva az x szerintit integrálva:
Hangsúlyozzuk, hogy itt két esetben a Newton-Leibniz-formulát használtuk a határozott integrál kiszámítására:
ahol F az f primitív függvénye (vagy határozatlan integrálja). Az eslő esetben az y változó szerepeltetése az integrál kiszámítását követően indokolatlanná vált, de az x megmaradt, amit tovább kellet integrálni az x változóra vonatkozóan. Fordított esetben szintén 4-et kapunk:
2. Példa
Korlátos, megszámlálható sok szakadási ponttal rendelkező függvény is integrálható:
| 8. gyakorlat | 10. gyakorlat |
![L^2[0,\pi]=\{f:[0,\pi]\to \mathbf{R}\mid ''f\quad\mathrm{Lebesgue\mbox{-}int.\mbox{-}hato\!'\,}''\}](/upload/math/f/6/c/f6c6c082f00f7589b656d593157db9bd.png)
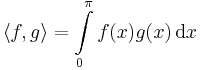
![f(x)=x,\quad x\in[0,\pi]\,](/upload/math/6/6/9/669cfa9c0ae10637390cc81f5b9b8b3d.png)
![L=\mathrm{Span}(\sin)\subseteq L^2[0,\pi]](/upload/math/f/8/0/f806d92c59a1a82a9023b27d6e1fdea0.png)
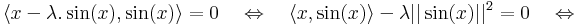
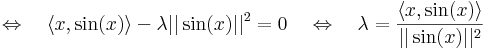
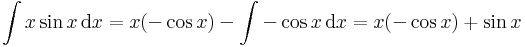
![\int\limits_{0}^\pi x\sin x\,\mathrm{d}x=[x(-\cos x)+\sin x]^\pi_0=\pi](/upload/math/2/a/0/2a0273844dc6505603a239f41f64f6f7.png)
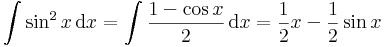
![||\sin(x)||=[\frac{1}{2}x-\frac{1}{2}\sin x]_0^\pi=\frac{\pi}{2}](/upload/math/d/0/6/d067b34159f2cf7d0cd1698c9ebd0ad4.png)
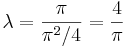
![\int\limits_{[a,b]\times[c,d]}f=\int\limits_{x=a}^b\left(\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\right)\mathrm{d}x=\int\limits_{x=a}^b\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\mathrm{d}x=\int\limits_{y=c}^d\left(\int\limits_{x=a}^b f(x,y)\;\mathrm{d}x\right)\mathrm{d}y](/upload/math/e/f/1/ef10affe1fac157d5fb4427a3a83163c.png)
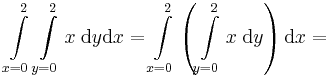
![=\int\limits_{x=0}^2[xy]_{y=0}^{2}\mathrm{d}x=\int\limits_{x=0}^2 2x\;\mathrm{d}x=[x^2]_{x=0}^{2}=4](/upload/math/4/d/7/4d76d92326d729d8a5d68cc30b7ab6c6.png)
![\int\limits_{a}^b f(x)\mathrm{d}x=[F(x)]_{a}^{b}=F(b)-F(a)](/upload/math/8/5/3/853da39029315b2aba44dce65c638884.png)
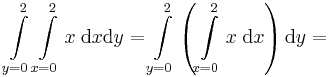
![=\int\limits_{y=0}^2\left[\frac{x^2}{2}\right]_{x=0}^{2} \;\mathrm{d}y=\int\limits_{y=0}^22\;\mathrm{d}y=[2y]_{y=0}^{2}=4](/upload/math/1/a/c/1ac20b7ea17e50cca88da80de185aa12.png)