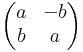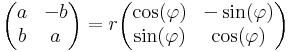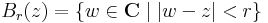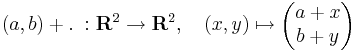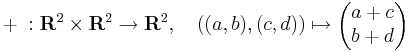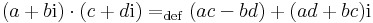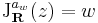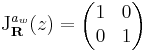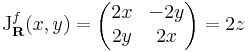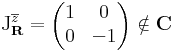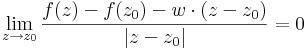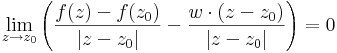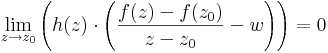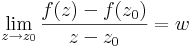Matematika A3a 2008/1. gyakorlat

A MathWikiből
(Változatok közti eltérés)
(→'''C'''-differenciálhatóság)
(→'''C'''-differenciálhatóság)
111. sor: 111. sor:
  
 
'''Feladat.''' Komplex deriválható-e: <math>\scriptstyle{f(z)=z\cdot\overline{z}}</math>, vagy a <math>\scriptstyle{f(z)=z^2\cdot\overline{z}}</math>?
 
'''Feladat.''' Komplex deriválható-e: <math>\scriptstyle{f(z)=z\cdot\overline{z}}</math>, vagy a <math>\scriptstyle{f(z)=z^2\cdot\overline{z}}</math>?
 +
 +
'''Feladat.''' Igazoljuk, hogy ha ''f'' korlátos komplex függvény a ''D'' &sube; '''C''' halmazon és lim<sub>w</sub>''g'' = 0, akkor lim<sub>w</sub> ''fg'' = 0. (w &isin; int D).

A lap 2008. szeptember 8., 23:59-kori változata

Matematika A3a 2008

Tartalomjegyzék

Komplex számkör unicitása és reprezentációi

C, azaz a komplex számok teste kétdimenziós valós vektortér. C elemei reprezentálhatók az R2 síkon, a következő megfeleltetésekkel:

\mathbf{C}\ni a+bi\equiv (a,b)\in \mathbf{R}^2

a vektortérműveletek pedig:

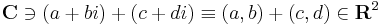\mathbf{C}\ni (a+bi)+(c+di)\equiv (a,b)+(c,d)\in \mathbf{R}^2 vektorösszeadás (a, b, c, d ∈ R)
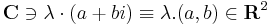\mathbf{C}\ni \lambda\cdot(a+bi)\equiv \lambda.(a,b)\in \mathbf{R}^2 valós számmal való szorzás (λ, a, b ∈ R)

A komplex számok körét a komplex szorzás tulajdonságai egyértelműsítik. C nem csak kétdimenziós valós vektortér, de a szorzással algebra is, sőt C az egyetlen kétdimenziós kommutatív, nullosztómentes valós algebra -- izomorfizmus erejéig. Sok megjelenési formája lehet a komplex számoknak, de bármely két reprezentáció olyan, hogy található olyan kölcsönösen egyértelmű leképezés köztük, mely lineáris és megtartja a szorzást is (azaz algebra izomorfizmus).

A nullosztómentesség és a kommutativitás jellemzően a mátrixalgebrákban nemtriviális tulajdonság. A komplex számok olyan lineáris leképezéseknek felelnek meg, melyek mátrixa

\begin{pmatrix} a & -b\\ b & a \end{pmatrix}

A komplex számok szorzása itt a mátrixszorzás.

Ezek tényleg az R2 forgatva nyújtásai, csak át kell térnünk trigonometrikus alakra:

\begin{pmatrix} a & -b\\ b & a \end{pmatrix}=r\begin{pmatrix} \cos(\varphi) & -\sin(\varphi)\\ \sin(\varphi) & \cos(\varphi) \end{pmatrix}

Topológia C-ben

C-ben, mint az R2 sík elemein tehát értelmezhetjük a gömbi környezeteket, mint az R2 sík pontjai körüli gömböket. Ezzel meg is kaptuk a C-beli nyílt halmazokat, azaz C topológiáját. A gömbök tehát a Gauss-számsík körlapjai:

B_r(z)=\{w\in \mathbf{C}\mid |w-z|< r\}

ahol z ∈ C, r > 0 valós szám.

Világos, hogy akármilyen R2-beli norma szerinti gömböket is választhattunk volna a C gömbjeinek, mert R2-ben minden norma ugyanazt a topológiát származtatja. Mi a ||.||2-t, azaz az euklideszi normát emeltük ki.

Folytonosság

Egy f : C \to C függvény folytonossága ezennel értelmezve van éspedig nem más, mint az R2-beli ||.||2 norma szerinti folytonosság. (HF: fogalmazzuk meg a C \to C függvények folytonosságának epszilon-deltás definícióját!)

Lineáris (jobban mondva R-lineáris), RN \to RM függvény folytonos, így a műveltek folytonosak lesznek:

(a,b)+.\;:\mathbf{R}^2\to\mathbf{R}^2,\quad(x,y)\mapsto\begin{pmatrix}a + x\\b + y\end{pmatrix}

és

+\;:\mathbf{R}^2\times\mathbf{R}^2\to\mathbf{R}^2,\quad((a,b),(c,d))\mapsto\begin{pmatrix}a + c\\b + d\end{pmatrix}

folytonosak (az egyik az ||.||C,||.||C, a másik a ||.||C×C,||.||C normapárok szerint).

Mi több, a komplex számok legjellegzetesebb algebrai-topológiai tulajdonsága, hogy a komplex számok

(a+b\mathrm{i})\cdot (c+d\mathrm{i})=_{\mathrm{def}}(ac-bd)+(ad+bc)\mathrm{i}

szorzása is mindkét változójában R-lineáris, így folytonos.

Szemléletessé tehetjük a két fenti példát, ha a két művelet geometriai jelentését tekintjük. A hozzáadás eltolás, a komplex számmal szorzás forgatva nyújtás, így a gömbi környzeteket olyan alakzatokba képezik, melyek geometriai okokból mutatják a folytonosságot:

w+B_r(z_0)=B_r(w+z_0)\,
w\cdot B_r(z_0)\subseteq B_{r\cdot|w|}(wz_0)

R-differenciálhatóság

Egy f : C \to C függvény abban az értelemen R-differenciálható, ahogy egy RN \to RM függvény differenciálhatóságát definiáltuk. Ekkor például a hozzáadás, mint affin függvény R-differenciálható, és R-differenciálja az identitás:

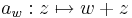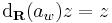
a_w:z\mapsto w+ z\, akkor \mathrm{d}_\mathbf{R}(a_w)z=z

A komplex számmal szorzás R-differenciálját közvetlenül a definíciójából számíthatjuk ki:

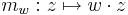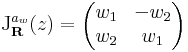
m_w:z\mapsto w\cdot z\, akkor \mathrm{J}_\mathbf{R}^{a_w}(z)=\begin{pmatrix} w_1 & -w_2\\ w_2 & w_1 \end{pmatrix}

Rendkívül érdekes észrevétel tanúi lehetünk ekkor. z \mapsto w\cdot z R-deriváltja maga w komplex számnak megfelelő mátrix, azaz

\mathrm{J}_\mathbf{R}^{a_w}(z)=w

ha mátrixreprezentációt veszünk. Sőt, visszanézve ez az összeadásra is igaz:

\mathrm{J}_\mathbf{R}^{a_w}(z)=\begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}

Feladat. Számítsuk ki az f(z) = z2 R-differenciálját!

Legyen z = x + i y. Ekkor z2 = x2 - y2 +i(2xy)

\mathrm{J}_\mathbf{R}^f(x,y)=\begin{pmatrix} 2x & -2y\\ 2y & 2x \end{pmatrix}=2z


Feladat. Számítsuk ki az 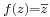\scriptstyle{f(z)=\overline{z}} R-differenciálját!


Ha z = x + i y, akkor 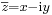\scriptstyle{\overline{z}=x-\mathrm{i}y}, így:

\mathrm{J}_\mathbf{R}^\overline{z}=\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}\notin\mathbf{C}

És ezzel már ki is mondhatjuk a Cauchy-Riemann-féle szükséges feltételt:

Annak a szükséges feltétele, hogy az f:R2 \to R2 R-differenciálható függvény differenciálja egy komplex szám mátrixreprezentációja legyen, az, hogy:
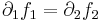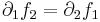
\partial_1 f_1=\partial_2 f_2 és \partial_1 f_2=\partial_2 f_1

C-differenciálhatóság

A fenti példa motiválja a C-differenciálhatóság fogalmát. Legyen a szituáció az előbbi, azaz legyen f(z) totálisan differenciálható (mint kétváltozós függvény) a z0 pontban és a Jacobi-mátrixa ott legyen a w ∈ C szám mátrixreprezentációja. Ekkor

\lim\limits_{z\to z_0}\frac{f(z)-f(z_0)-w\cdot (z-z_0)}{|z-z_0|}=0

Itt w\cdot(z-z0) egyfelől a mátrixszorzás, másfelől a komplex szorzás. Ekkor:

\lim\limits_{z\to z_0}\left(\frac{f(z)-f(z_0)}{|z-z_0|}-\frac{w\cdot (z-z_0)}{|z-z_0|}\right)=0

Ha h(z)=(z-z0)/|z-z0|, ami a komplex "egységgömbön" "futó" függvény, akkor a komplex szorzás tulajdonságai miatt:

\lim\limits_{z\to z_0}\left(h(z)\cdot \left(\frac{f(z)-f(z_0)}{z-z_0}-w\right)\right)=0

Innen a kovetkező gondolatunk támadhat. Teljesen az egyváltozós valós derivált tulajdonságait mutató deriváltfogalmat kapunk, ha bevezetődne a következő


Definíció - Komplex differenciálhatóság, komplex derivált - Legyen f a z0 egy környezetében értelmezett függvény. Azt mondjuk, hogy f C-deriválható z0-ban és deriváltja a w szám, ha

\lim\limits_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}=w

Most gondoljuk végig, hogy milyen kapcsolatban van az R'- és a C-deriválhatóság. Ha a fenti gondolamenetet felefelé nézzük, akkor a h(z) korlátossága miatt a "korlátos szor nullához" tartó függvényt kapunk, így a szorzat határértéke 0. Persze ehhez kellene a "korlátos szor nullához tartó" lemma komplex szorzásra.

Ha lefelé gondolkodunk, akkor indirekten kell eljárnunk. Tegyük fel, hogy a második tényező nem nulla határértékű. Amikor nem létezik, vagy nem az adott szám a határérték, akkor "cáfoló" sorozatot szoktunk megadni. Az átviteli elv miatt létezik olyan z(n) konvergens komplex sorozat, mely nem a 0-hoz tart. De a h(z(n)) ekkor az egységkörön van, így a szorzat biztosan "elerüli a nullát" (az abszolút értéke nem a 0-hoz tart). Következésképpen:

Tétel. A definícióbeli f pontosan akkor komplex diffható, ha diffható és a deriváltja komplex szám (mátrix reprezentációja). Továbbá f pontosan akkor komplex diffható, ha diffható és a parciális deriváltjai teljesítik a Cauchy-Riemann-egyenleteket.

Feladat. Komplex deriváljuk az f(z) = zn függvényt!

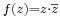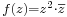Feladat. Komplex deriválható-e: \scriptstyle{f(z)=z\cdot\overline{z}}, vagy a \scriptstyle{f(z)=z^2\cdot\overline{z}}?

Feladat. Igazoljuk, hogy ha f korlátos komplex függvény a D ⊆ C halmazon és limwg = 0, akkor limw fg = 0. (w ∈ int D).

A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Matematika_A3a_2008/1._gyakorlat&oldid=3903”
Személyes eszközök