Matematika A3a 2008/1. gyakorlat
Tartalomjegyzék |
Differenciálegyenletek
Legyen F:I×J R korlátos és zárt téglalapon értelmezett folytonos kétváltozós függvény. Az
R korlátos és zárt téglalapon értelmezett folytonos kétváltozós függvény. Az
- y ' = F(x,y)
elsőrendű közönséges differenciálegyenlet megoldásainak nevezzük az olyan y:K J függvényeket, melyekre
J függvényeket, melyekre
- 1) K⊆I intervallum,
- 2) y differenciálható függvény és
- 3) minden x ∈ K számra y'(x)=F(x,y(x)).
Ha (x0,y0)∈I×J, akkor az egyenlet y0 = y(x0) kezdeti feltételt kielégítő partikuláris megoldásának nevezzük az olyan megoldásokat, melyekre y0 = y(x0). Adott kezdeti feltételt kielégítő megoldás keresését kezdeti érték problémának vagy Cauchy-problémának nevezzük. Az egyenlet összes megoldása az egyenlet összes megoldása.
Integrálgörbe, görbesereg, általános megoldás
Az elsőrendű közönséges differenciálegyenlet megoldásának keresése geometriailag a következőket jelenti. Adott koordinátasíkon egy téglalap, melynek minden pontjához az F függvény egy számot (tkp. meredekséget) rendel. Ez az iránymező. Keresünk olyan függvénygörbéket, melyek deriváltja (érintőjének meredeksége) az adott pont abszciszájában éppen az F függvény azon pontbeli értéke. Az ilyen függvénygörbékhez tartozó egyváltozós függvények az egyenlet megoldásai, magukat a görbéket pedig az egyenlet integrálgörbéinek hívjuk.
1. Számpélda.
- (diff)
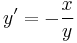
Bármi is legyen a megoldás, az nem vehet fel 0 értéket, mert az ismeretlen függvény a nevezőben szerepel. Látható, hogy az (x,y) vektor +90 fokos elforgatottja az F(x,y) értéke. Ebbe az iránymezőbe belesimul a kör:
- (impl)
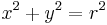
Az ilyen egyenlet által leírt függvénygörbe valóban a (diff) megoldását ábrázolja (feltéve, hogy y differenciálható és nem veszi föl a nullát).
Most megmutatjuk, hogy az (impl) differenciálható implicit függvényei megoldásai (diff)-nek. A differenciálható implicit függvénye (impl)-nek olyan intervallumon értelmezett y=y(x) diff.-ható függvény, melyre minden x∈Dom(y)-ra:
valamely r-re. Ha tehát van (impl)-nek y(x) megoldása, akkor az implicit deriválás szabályai szerint:
tehát y valóban (diff) megolása. A körívek tehát integrálgörbéi az egyenletnek. Az integrálgörbék ráadásul paraméteres görbesereggé állnak össze, melyekben a paraméter a kör sugara.
(diff) megoldásai azonban ugyanígy megoldásai (impl)-nak. Az a szerencsénk, hogy megsejtettük, hogy (impl) az egyenlet integrálja, ezért ezt már nem kell előállítanunk. Legyen y olyan, hogy 2x+2y(x)y'(x)≡0 és y0=y(x0). Az implicit deriválás miatt tudjuk, hogy
deriváltja, azaz 2x+2y(x)y'(x), azonosan nulla. Az integrálszámítás alaptétele szerint tehát g (az I minden korlátos és zárt L intervallumán) konstans függvény:
r2=C-t pedig kijelöli y0=y(x0).
[Az integálszámítás alaptétele abban a gyenge formában, ahogy mi most használtuk ez: ha a nyílt intervallumon értelmezett folytonosan differenciálható g:I R függvény deriváltja azonosan nulla, akkor ez a függvény minden zárt és korlátos intervallumon konstans. Ez közvetlen következménye a Lagrange-féle középértéktételnek. Az erősebbb alak szerint g-ről elég feltenni, hogy Lipschitz-függvény és a deriáltja majdnem mindenhol nulla.]
R függvény deriváltja azonosan nulla, akkor ez a függvény minden zárt és korlátos intervallumon konstans. Ez közvetlen következménye a Lagrange-féle középértéktételnek. Az erősebbb alak szerint g-ről elég feltenni, hogy Lipschitz-függvény és a deriáltja majdnem mindenhol nulla.]
Általánosított fogalmak. Azt mondjuk, hogy a differenciálegyenlet általános megoldását (a H⊆I×J kezdeti feltétel halmazon) a Φ(x,y,C)=0 egyenletű egyparaméteres görbesereg szolgáltatja (vagy az egyenlet általános megoldását az előbbi implicit egyenlet adja meg), ha minden (H-beli) (x0,y0) kezdeti feltételre van egyetlen olyan C valós paraméter, hogy rögzített C-re a Φ(x,y,C)=0 egyenlet (x0,y0) ponthoz tartozó implicit megoldása a differenciálegyenlet kezdeti feltételt kielégítő megoldása.
Az egyenlet explicit általános megoldása (a H⊆I×J halmazon ) a Ψ:K×R J paraméteres függvény, ha minden (H-beli) kezdeti feltételhez egyértelműen létezik olyan C, melyre y=Ψ(.,C) a szóban forgó kezdeti feltételt kielégítő megoldása az egyenletnek.
J paraméteres függvény, ha minden (H-beli) kezdeti feltételhez egyértelműen létezik olyan C, melyre y=Ψ(.,C) a szóban forgó kezdeti feltételt kielégítő megoldása az egyenletnek.
Tegyük föl, hogy a Φ(x,y,C)=0 implicit egyenlettel megadott görbesereg elemei megoldásai egy differenciálegyenletnek. Ha Φ minden változója szerint (tehát a paraméter szerint is) folytonosan parciálisan differenciálható, akkor annak az elégséges feltétele, hogy C egyértelműen kifejezhető legyen az, hogy Φ C-szerinti deriváltja sehol se legyen nulla. Ezt a feltételt az implicitfüggvény tétele biztosítja.
Szeparábilis differenciálegyenlet
A legegyszerűbb differenciálegyenlet az y'=f(x), ami lényegében primitívfüggvénykeresés. Tudjuk, hogy (folytonos f esetén) mindig van ennek megoldása, éspedig az integrálfüggvény az, de ez nem feltétlenül kapható meg elemi függvények segítségével "kézzel fogható" zárt alakban. Az előző számpélda arról árulkodott, hogy a diffegyenlet megoldásához kell egy egyenlet, melynek implicit megoldásai az differenciálegyenlet megoldásai lesznek. Ezt az implicit egyenletet konstruktív módon nem mindig lehet megtalálni. (Az explicitet meg pláne nem.)
Általánosabb esetben a közönséges elsőrendű differenciálegyenletek megoldását két startégiával kereshetjük meg. Az egzakt differenciálegyenlet és a szeparálás. Most a szeparábilis egyenletek megoldását nézzük meg.
2. Feladat. Milyen függvények elégítik ki az alábbi differenciálegyenletet?
Megoldás. Nyilván a megoldás sehol sem vehet föl nulla értéket, mert akkor
ott nem lenne értelmezve.
A mechanikus megoldási eljárás annak az egyenletnek a legyártásához, melynek implicit megoldásai a szeparábilis egyenlet megoldásai lesznek a következő. Ha van megoldás, akkor nyilván
ez az implicit általános megoldás és
az explicit általános megoldás.
Olyan K R differenciálható függvények a megoldások, melyek hozzárendelési utasítása a fenti és nem veszik fel a nulla értéket. A megoldás mechanikus megkeresése után tehát olyan K⊆R intervallumokra kell szorítkoznunk, ahol az y(x) nem vesz fel nulla értéket és a 7. gyök alatt nincs nulla (ahol az nem lenne differenciálható).
R differenciálható függvények a megoldások, melyek hozzárendelési utasítása a fenti és nem veszik fel a nulla értéket. A megoldás mechanikus megkeresése után tehát olyan K⊆R intervallumokra kell szorítkoznunk, ahol az y(x) nem vesz fel nulla értéket és a 7. gyök alatt nincs nulla (ahol az nem lenne differenciálható).
Egzisztencia és unicitás
Tétel. Legyen f : I  R, g: J
R, g: J  R intervallumon értelmezett folytonos függvények, ahol g sehol sem nulla. Az
R intervallumon értelmezett folytonos függvények, ahol g sehol sem nulla. Az
szeparábilis diffegyenlet összes megoldása
alakú, ahol G az 1/g egy integrálfüggvénye, F az f-é.
Bizonyítás. Tegyük fel, hogy van megoldás és ennek értelmezési tartománya a K⊆I halmaz. Ekkor
A helyettesítéses integrálás szabálya szerint
azaz
ahol G az 1/g egy integrálfüggvénye, F az f-é. Mivel G deriváltja g és a derivált nem ugrik (Darboux-tétel), ezért G szigorúan monoton, tehát G injektív, azaz az y kifejezhető:
Az implicitfüggvény-tételből az is kiderül, hogy az Φ(x,y)=G(y)-F(x)-C függvény folytonosan differenciálható és y szerinti deriváltja nem nulla, így lokálisan létezik implicit függvénye bármely pontban és deriváltja:
3. Feladat. Oldjuk meg az 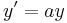 egyenletet.
egyenletet.
Mo.y≡0 megoldás. Ha semmilyen pontban y nem nulla, akkor ln |y|= ax +C, |y|=Keax, ennek differenciálható implicit függvényei (a Bolzano-tétel miatt): y=ceax ahol c nemnulla valós szám; ha c=0 is megengedett, akkor az y=0 is beilleszthető a paraméteres megoldások közé. Valójában a feladat becsapás, mert ez nem szeparábilis egyenlet. Szeparálással megkaphatók megoldások, és mivel lineáris, ezért a megoldásai egydimenziós lineáris teret alkotnak, azaz egy nemnulla megoldásból az összes megoldás egy konstans szorzóval megkapható, tehát y=ceax az összes megoldás. Továbbá az alábbi C--L-feltétel miatt a 0 értékű megoldás is egyértelmű, azaz ha valahol 0 a megoldás, akkor az csak az azonosan nulla lehet.
4. Feladat. 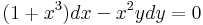 Minden olyan intervallumon, melynek a 0 nem eleme szeparálva:
Minden olyan intervallumon, melynek a 0 nem eleme szeparálva:
Peano- és Cauchy--Lipschitz-feltétel
Tétel -- Peano-féle egzisztenciatétel -- Ha az f(x,y)=y' egyenlet olyan, hogy az f egy (x0,y0) pont környezetében folytonos, akkor van az y(x0)=y0 kezdeti feltételnek eleget tévő partikuláris megoldása.
Megmutatjuk, hogy a folytonossági kitétel szükséges. Tekintsük a 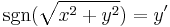 egyenletet. Nyilván ennek nincs megoldása a (0,0)-ban, mert ha lenne, akkor a deriváltja ugranak, márpedig intervallumon deriválható differenciálható függvény deriváltjának nem lehet ugrása.
egyenletet. Nyilván ennek nincs megoldása a (0,0)-ban, mert ha lenne, akkor a deriváltja ugranak, márpedig intervallumon deriválható differenciálható függvény deriváltjának nem lehet ugrása.
Tétel -- Egzisztencia-unicitás tétel, gyenge verzió, lokális alak -- Ha az U nyílt halmazon értelmezett f(x,y) folytonosan parciálisan differenciálható, akkor minden U-beli kezdeti feltételhez egyértelműen létezik az y'=f(x,y)-nak a kezdeti feltételnek megfelelő megoldása.
Cauchy--Lipschitz-feltétel, erős verzió, globális alak. A tétel akkor is igaz, ha f-re nem a folytonos deriválhatóságot, hanem csak a folytonosságot és az egységes Lipschitz-feltételt tesszük fel, azaz, hogy létezik olyan L szám, hogy minden (x,y1),(x,y2)∈U-ra
Ilyenkor globális állítás is megfogalmazható: minden U-beli kompakt K halmazhoz és az ennek belsejében lévő kezdeti ponthoz létezik egyetlen megoldása az y'=f(x,y) differenciálegyenletnek, mely áthalad a ponton és a megoldás grafikonja a K halmazból kilép.
Feladatok
a) Mi az általános megoldása?
b) Hány megoldása van az alábbi KÉF-nak? Ha több van, mondjunk legalább kettőt!
![y'=\sqrt[3]{y}](/upload/math/a/a/8/aa8ead75b510de8d5e82073a3a722bde.png) ,
, 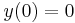
Mo. a) Minden olyan kezdeti feltételhez, melyben y nem nulla van egyértelmű megoldás, éspedig
b)
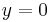 és
és 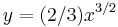
| 2. gyakorlat |
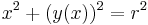
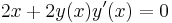
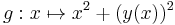
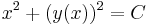
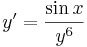
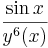
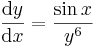
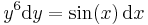
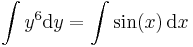
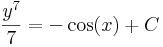
![y(x)=\sqrt[7]{-7\cos(x)+C}\,](/upload/math/e/2/d/e2d7f66e9664a8ea1ef763c670f9b58c.png)
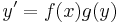
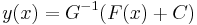
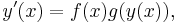
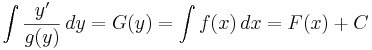
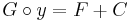
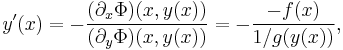
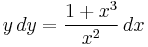
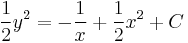
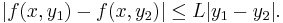
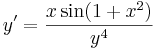
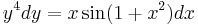
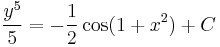
![y(x)=\sqrt[5]{-\frac{5}{2}\cos(1+x^2)+5C}](/upload/math/0/c/4/0c4a0431bfe9a72fe6e2a4399d8d3913.png)