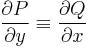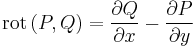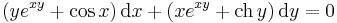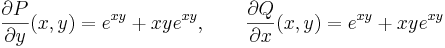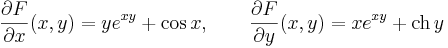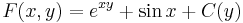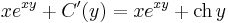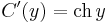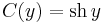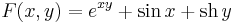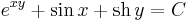Matematika A3a 2008/2. gyakorlat
Tartalomjegyzék |
Gyakorlatok kezdeti érték feladatra
1. Oldjuk meg az
egyenletet az
- a)
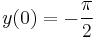
- b)
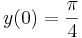
- c)
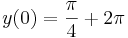
kezdeti feltételek mellett!
Mo. a) Ehhez egy konstans megoldás tartpzik és nincs másik a (0,-π/2)-n áthaladó, mert az y szerinti parciális derivált korlátos.
b) Az általános megoldásból keressük a kezdeti feltételt kielégítő megoldást:
Az implicit egyenlet:
- cos − 3y = x3 + 3C
Ha x=0 és y=π/4, akkor
és
c) ugyanez + 2π
HF. Oldjuk meg az y' = sin(x) yln(y) egyenletet az
- a) y(0)=1,
- b) y(0)=e
kezdeti feltételek mellett!
Függvényegyenletek
2. feladat. Van-e nemdifferenciálható, de folytonos megoldása az 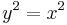 függvényegyenletnek?
Mo. Igen: y(x)=|x| nemdifferenciálható, de folytonos megoldása.
függvényegyenletnek?
Mo. Igen: y(x)=|x| nemdifferenciálható, de folytonos megoldása.
3. Feladat. Hány megoldása van az |f(x)|=ex R-en? Hány diffható ebből? Mo. Végtelen sok megoldása van, pl.: minden n természetes számhoz található mo., melyek egymáshoz páronként különbözők: f(x)=ex, ha x nem az n természetes szám és -ex, ha x az n természetes szám. Ebből kettő diffható akad: ex, -ex, ami a Bolzano-tételből következik. Ha ugyanis lenne nem csak poz. és nem csak neg. mo., akkor a 0-t is felvenné, ami lehetetlen, mert az exp. függvénynek nincs nulla értéke.
Homogén fokszámú egyenletek
Az F(x,y) n-homogén függvény, ha minden λ esetén
- F(λx,λy) = λnF(x,y).
Az y'=F(x,y) egyenlet homogén, ha F(x,y) 0-homogén.
Homogén egyenleteknél az y=ux helyettesítés vezet célra. Akkor
- y'=u'x+u
Feladat. (2x+y)dx + (y+x)dy =0 Homogén, mert
jobb oldala 0-homogén:
Egzakt differenciálegyenlet
Definíció
Legyen U ⊆ R2 nyílt halmaz és P,Q: U  R folytonos függvények, Q sehol sem nulla. Azt mondjuk, hogy az
R folytonos függvények, Q sehol sem nulla. Azt mondjuk, hogy az
differenciálegyenlet egzakt, ha létezik olyan F: U  R folytonosan differenciálható függvény, hogy
R folytonosan differenciálható függvény, hogy
Számpélda. Az
egyenlet egzakt, mert az F(x,y)=x2+y2 függvény olyan, hogy ∂xF(x,y)=2x, ∂yF(x,y)=2y, mármint az
alakjában egzakt.
Elméleti példa. Minden
alakú szeparábilis differenciálegyenlet egzakt, hiszen ha g integrálfüggvénye G, akkor
Alkalmas tehát az alábbi függvény:
Jelen esetben a G függvény deriváltja (G'=g) sehol sem nulla folytonos függvény, ezért szigorúan monoton. Emiatt kifejezhető y éspedig:
Megjegyzés. A megoldásokat implicit módon adja meg az
egyenlet. Mivel
ezért az implicitfüggvény-tétel miatt y-t "ki lehet fejezni". Érdemes felelevenítenünk magát az implicitfüggvény-tételt:
Implicitfüggvény-tétel -- Ha a Φ: I×J  R folytonosan differenciálható függvény az (x0,y0) ∈ int(I×J) pontban teljesíti a ∂Φ/∂y ≠ 0 feltételt, akkor a (x0,y0) pont egy környezetében egyértelműen létezik az Φ(x,y)=Φ(x0,y0) egyenletnek az (x0,y0) ponton áthaladó implicit függvénye, azaz az x0 egy K⊆I környezetében értelmezett, J-beli értékű y deriválható függvény, melyre minden x ∈ K esetén:
R folytonosan differenciálható függvény az (x0,y0) ∈ int(I×J) pontban teljesíti a ∂Φ/∂y ≠ 0 feltételt, akkor a (x0,y0) pont egy környezetében egyértelműen létezik az Φ(x,y)=Φ(x0,y0) egyenletnek az (x0,y0) ponton áthaladó implicit függvénye, azaz az x0 egy K⊆I környezetében értelmezett, J-beli értékű y deriválható függvény, melyre minden x ∈ K esetén:
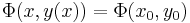 ,
, 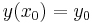
és ennek deriváltja minden x ∈ K-ban:
Egzisztencia- és unicitástétel
Tétel. Legyenek P és Q az U ⊆ R2 nyílt halmazon értelmezett folytonos valós függvények, Q sehol se nulla, grad F = (P,Q) valamely F: U  R folytonosan differenciálható függvénnyel és (x0,y0) ∈ U. Ekkor
R folytonosan differenciálható függvénnyel és (x0,y0) ∈ U. Ekkor
1) az
- (ex) y'=-P/Q
egyenletnek egyértelműen létezik az y0 = y(x0) kezdeti feltételt kielégítő y lokális megoldása és
2) az
- (impl) F(x,y) = F(x0,y0)
egyenlet (x0,y0)-on áthaladó egyetlen lokális implicit függvénye az (ex) egyenlet y(x0) = y0 kezdeti feltételt kielégítő egyetlen lokális megoldása.
Biz. 1) Egzisztencia. Belátjuk, hogy (impl) egyetlen (x0,y0)-on áthaladó implicit függvénye megoldása az (ex) egyenletnek.
így az implicitfüggvény-tétel szerint, egyértelműen létezik F-nek y=y(x) implicit függvénye az adott pont egy környezetében és ennek deriváltja az értelmezési tartományának minden pontjában:
tehát y az (ex) differenciálegyenletnek is megoldása, és ez kielégíti a kezdeti feltételt.
Unicitás. Tegyük fel, hogy létezik megoldása a kezdeti érték feladatnak. Legyen egy tetszőleges megoldása y, azaz
Ez az egyenlet a grad F = (P,Q) miatt előáll
alakban. Most belátjuk, hogy y (impl)-nek implicit megoldása. Az összetett függvény differenciálási szabálya miatt ( d(F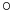 G)(x,y)=dF(G(x,y))
G)(x,y)=dF(G(x,y))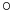 dG(x,y) ) az előző egyenlet a következő formában is írható:
dG(x,y) ) az előző egyenlet a következő formában is írható:
x értékei egy intervallumból kerülnek ki, ezért az integrálszámítás alaptétele szerint az x  F(x,y(x)) egy konstans függvény. De a feltétel szerint y(x0) = y0 teljesül, ezért x
F(x,y(x)) egy konstans függvény. De a feltétel szerint y(x0) = y0 teljesül, ezért x  y(x) egy (x0,y0)-on áthaladó implicit függvénye az F(x,y)=F(x0,y0) egyenletnek. Ez az utóbbi azonban egyértelműen van meghatározva, ezért a kezdeti érték feladat minden megoldása egybeesik ezzel az implicit függvénnyel, azaz a megoldás egyértelmű.
y(x) egy (x0,y0)-on áthaladó implicit függvénye az F(x,y)=F(x0,y0) egyenletnek. Ez az utóbbi azonban egyértelműen van meghatározva, ezért a kezdeti érték feladat minden megoldása egybeesik ezzel az implicit függvénnyel, azaz a megoldás egyértelmű.
2) Az implicitfüggvény tételében adott egyetlen implicit függvény az 1) egzisztencia része miatt megoldása (ex)-nek és 1) unicitás része miatt ez az egyetlen megoldása (ex)-nek.
Az egzaktság jellemzése
Megjegyzés. Az egzakt differenciálegyenletet még
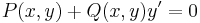 ill.
ill. 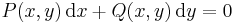
alakban is szokás írni.
Ez utóbbi egyenletről azt is mondják, hogy akkor egzakt, ha a P(x,y)dx + Q(x,y)dy kifejezés "teljes differenciál", amin azt értik, hogy létezik olyan F(x,y) függvény, melynek teljes differenciálja:
Ezt a mai jelölésekkel a következőképpen írjuk. Egy F kétváltozós függvény teljes differenciálja egy lineáris leképezés, mely a sztenderd {(1,0),(0,1)} bázisban felírt koordinátáival nem más, mit a parciális deriváltjainak sormátrixa:
Emiatt a (C) feltétel a következő alakban is írható:
![[\mathrm{d}F]=\left[P,Q\right]\,](/upload/math/3/4/3/343e00846494e553e629c9e57344a211.png) ill.
ill. ![\mathrm{grad}\,F=[P,Q]\,](/upload/math/4/f/9/4f9b9ba5601098c77e15e1f242d50948.png)
Tehát az egzakt egyenletben a (P,Q) vektormező (vektorértékű függvény) potenciálos. Innen hasznos jellemzést kapunk az egzaktságra a vektoranalízisbeli ismereteinkből.
Tétel. Legyen U egyszeresen összefüggő nyílt halmaz, P,Q: U  R folytonosan differenciálható függvények (Q sehol sem nulla). A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha
R folytonosan differenciálható függvények (Q sehol sem nulla). A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha
Az F függvényt, az Pdx + Qdy = 0 egyenlet integráljának nevezzük.
Ezt a tételt jól ismerjük és a bizonyítását a vektoranalízisben vettük.
Megjegyzés. 1) A feltétel nem más, mint az, hogy a (P,Q) síkbeli vektormező rotációja azonosan nulla. Ugyanis a rotáció a síkbeli (P,Q) vektormező esetén:
2) Bár a szeparábilis egyenlet egzakt, a fenti feltétel az egzaktság ellenőrzésére sokkal szigorúbb mint a szeparábilis egyenlet megoldhatóságának feltétele.
Példák
Oldjuk meg az
differenciálegyenletet!
Mo.
Tehát egzakt. Az egyenlet első integrálját megkapjuk, ha megoldjuk az
parciális differenciálegyenlet-rendszert.
Az első egyenletből:
A második egyenlet miatt:
azaz
Innen a C(y)-ra egy partikuláris megoldás:
Azaz
Ez valóban teljesíti a grad F = [P,Q] feltételt, így az első integrál:
Feladat. Oldjuk meg az y'=(ycos(xy)+1)/-xcos(xy) az y(1)=0 kezdeti feltétel mellett! Mo. (ycos(xy)+1)dx + xcos(xy)dy=0 Integráljuk mindkét függvényt: F(x,y)=x+ysin(xy)/y+C1(y)=xsin(xy)/x+C2(x). Innen F(x,y)=sin(xy)+x. Ez valóban megoldás és az implicit általános megoldás sin(xy)+x=C. A kezdeti feléttelt kielégítő megoldás: sin(xy)+x=1, ahonnan egy lokális megoldás az x∈(0,2)-beli: sin(xy)=1-x, xy=arc sin(1-x), y(x)=arc sin(1-x)/x
| 1. gyakorlat |
| 3. gyakorlat |
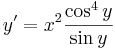
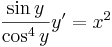
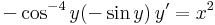
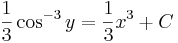
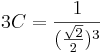
![y(x)=\mathrm{arccos}\frac{1}{\sqrt[3]{x^3+\frac{24}{(\sqrt{2})^3}}}](/upload/math/2/d/0/2d00fc36a69b3e76ac5fef5e80c7a2a3.png)
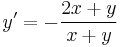
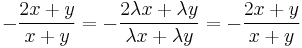
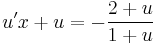
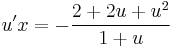
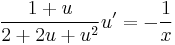
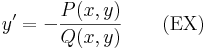
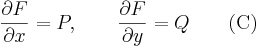
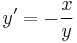
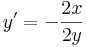
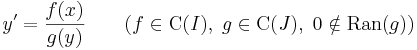
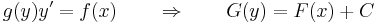
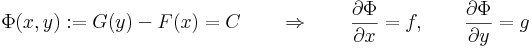
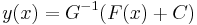
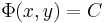
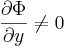
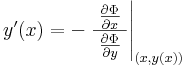
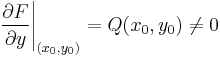
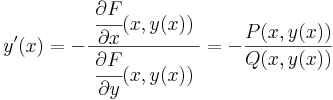
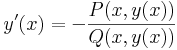
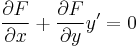
![(F(x,y(x)))'=[\mathrm{grad}\,F|_{(x,y(x))}]\cdot\begin{bmatrix}x'\\y'(x)\end{bmatrix}=\frac{\partial F}{\partial x}|_{(x,y(x))}+y'\frac{\partial F}{\partial y}|_{(x,y(x))}\equiv 0\,](/upload/math/6/a/0/6a01c3a741e5c2d447b6e0254117aa36.png)
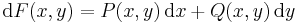
![[\mathrm{d}F(x,y)]=\mathrm{grad}\,F(x,y)=\left[\;\frac{\partial F}{\partial x}\;,\;\frac{\partial F}{\partial y}\;\right]](/upload/math/6/d/6/6d677f005d45feb13decbeb9f8433c81.png)