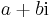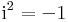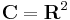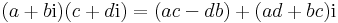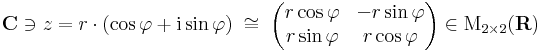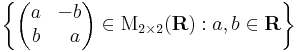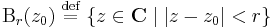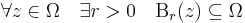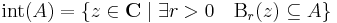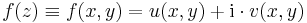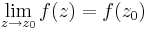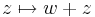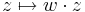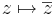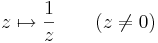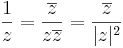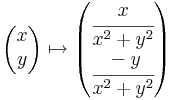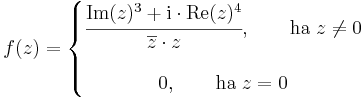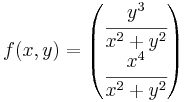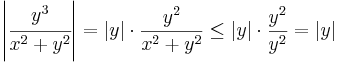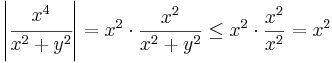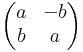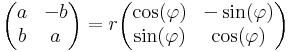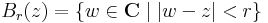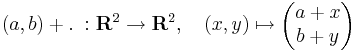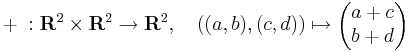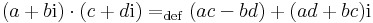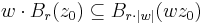Matematika A3a 2008/1. gyakorlat
Mozo (vitalap | szerkesztései) (→'''R'''-differenciálhatóság) |
Mozo (vitalap | szerkesztései) |
||
| 1. sor: | 1. sor: | ||
''<sub><[[Matematika A3a 2008]]</sub>'' | ''<sub><[[Matematika A3a 2008]]</sub>'' | ||
| + | ==Komplex számkör és reprezentációi== | ||
| + | A komplex számok '''C''' halmazát és műveleteit legalább három, lényegesen más szemszögből lehet láttatni. A meghatározottság kedvéért összefoglaljuk a komplex számok legfontosabb algebrai tulajdonságait. Nem térünk ki minden egyes műveleti tulajdonságra, ezek megtalálhatók a komplex számok algebráját leíró tankönyvekben. | ||
| + | |||
| + | ===Algebrai modell=== | ||
| + | A komplex számok olyan | ||
| + | :<math>a+b\mathrm{i}\,</math> | ||
| + | alakú formális kifejezések, ahol ''a'' és ''b'' valós számok, i pedig azzal a speciális tulajdonsággal rendelkezik, hogy | ||
| + | :<math>\mathrm{i}^2=-1\,</math> | ||
| + | A komplex számok halmazát a '''C''' szimbólummal jelöljük. Akárcsak a legfeljebb elsőfokú ''a'' + ''bx'' alakú polinomok esetén, a '''C'''-t alkotó formális kifejezések között is értelmezhetjük az összeadást és a szorzást. Ezeket pontosan úgy definiáljuk, mint az ''a'' + ''bx'' alakú polinomok összegét és szorzatát, azzal a specialitással, hogy ahol a polinomok a szorzást követően másodfokúvá válnak, ott a komplex számok az i<sup>2</sup>=-1 egyenlőség miatt visszaérkeznek az ''a'' + ''b''i alakú kifejezések körébe. Ezért lesz '''C''' zárt arra a szorzásra, amit a polinomok mintájára definiálunk. | ||
| + | |||
| + | Már innen is látszik, hogy a komplex számok halmaza kétdimenziós valós test feletti vektortér. Kimondhatjuk tehát: | ||
| + | |||
| + | {|align="center" cellpadding="2" border="0" style="background-color: #daf2fe;" | ||
| + | |- | ||
| + | |'''Állítás.''' A '''C''' számkör a komplex számok | ||
| + | :(''a''+''b''i) + (''c''+''d''i) = (''a''+''c'') + (''b''+''d'')i összeadásával és a | ||
| + | :λ(''a''+''b''i) = λ''a'' + λ''b''i, a λ valós számmal való szorzással | ||
| + | kétdimenziós valós vektorteret alkotnak és így lineárisan izomorfak a valós számpárok '''R'''<sup>2</sup> vektorterével. | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | ===Halmazelméleti modell=== | ||
| + | Az algebrai modellben nem teljesen világos, hogy mi is az i elem. Az előző állítás azonban lehetőséget biztosít arra, hogy konkrétan megadjuk a komplex számok halmazát mindenféle olyan kifejezés használata nélkül, mint "formális kifejezés" stb. (Valójában persze az algebrai modell is jól értelmezett módon adja meg a komplex számok halmazát, ha az ''a'' + ''b''i alakú formális kifejezéseken az '''R'''[X] polinomgyűrűnek az (1+X<sup>2</sup>) polinommal történő maradékos osztásának maradékait értjük). | ||
| + | |||
| + | A számpár reprezentációban: | ||
| + | :<math>\mathbf{C}=\mathbf{R}^{2}\,</math> | ||
| + | az összeadás az '''R'''<sup>2</sup>-beli vektorösszeadás, a szorzás, pedig a | ||
| + | :<math>(a+b\mathrm{i})(c+d\mathrm{i})=(ac-db)+(ad+bc)\mathrm{i}\,</math> | ||
| + | művelet, mely természetesen a "polinomszorzásnak" az előző állításbeli izomorfizmus által létesített képe. | ||
| + | |||
| + | Ez az interpretáció azért fontos, mert explicitté teszi, hogy a '''C''' örökli az '''R'''<sup>2</sup> topológiáját. | ||
| + | |||
| + | ===Geometriai modell=== | ||
| + | |||
| + | A szorzással együtt '''C''' egységelemes, nullosztómentes algebrát alkot (tehát vektortér és van egy mindkét változójában lineáris belső szorzás, melyben van egység és „nullával nem lehet osztani”). Felmerülhet a gyanúnk, hogy talán reprezentálhatjuk a komplex számokat a 2×2-es valós mátrixon M<sub>2×2</sub> ('''R''') algebrájának egy részalgebrájaként. Ezt a komplex számok trigonometrikus alakja segítségével tehetjük meg. Ismert, hogy a komplex számmal való szorzás forgatva nyújtás, azaz lineáris leképezés az '''R'''<sup>2</sup> síkon: | ||
| + | :<math>\mathbf{C}\ni z=r\cdot(\cos\varphi+\mathrm{i}\sin\varphi)\;\cong\; | ||
| + | \begin{pmatrix} | ||
| + | r\cos\varphi & -r\sin\varphi\\ | ||
| + | r\sin\varphi & r\cos\varphi | ||
| + | \end{pmatrix}\in \mathrm{M}_{2\times 2}(\mathbf{R})</math> | ||
| + | Világos, hogy ekkor az ''a'' + ''b''i kanonikus alakot használva a komplex számoknak megfelelő mátrixok halmaza: | ||
| + | :<math>\left\{\begin{pmatrix} | ||
| + | a & -b\\ | ||
| + | b & \;\;a | ||
| + | \end{pmatrix}\in\mathrm{M}_{2\times 2}(\mathbf{R}): a,b\in \mathbf{R}\right\}</math> | ||
| + | Ez a mátrixhalmaz kétdimenziós altér az M<sub>2×2</sub> ('''R''') algebrában, melyet például a közvetve onnan is láthatjuk, hogy forgatva nyújtások is alteret alkotnak a lineáris leképezések terében. | ||
| + | |||
| + | =='''C''' topológiája== | ||
| + | |||
| + | '''R'''<sup>2</sup> gömbi környezetei lesznek '''C''' gömbi környezetei. Általában, minden topologikus fogalom '''C'''-ben '''R'''<sup>2</sup>-re vezetünk vissza. Tehát, adott ''r'' > 0 valós számra és ''z''<sub>0</sub> ∈ '''C''' számra: | ||
| + | :<math>\mathrm{B}_r(z_0)\;\overset{\mathrm{def}}{=}\;\{z\in \mathbf{C}\mid |z-z_0|<r\}</math> | ||
| + | az ''r'' sugarú ''z''<sub>0</sub> középpontú nyílt gömbi környezet. Itt a | . | abszolútérték helyett, mely a || . ||<sub>2</sub> euklideszi norma, elvileg '''R'''<sup>2</sup> bármelyik normája alkalmas lenne, hisz véges dimenziós normált térben minden norma ekvivalens, azaz ugyanazokat a nyílt halmazokat határozzák meg. Szokásos módon értelmezettek az előbb említett nyílt halmazok is. Ω ⊆ '''C''' '''nyílt''', ha minden pontjával együtt, annak egy nyílt gömbi környezetét is tartalmazza: | ||
| + | :<math>\forall z\in \Omega\quad \exists r>0\quad \mathrm{B}_r(z)\subseteq \Omega</math> | ||
| + | Egy ''A'' ⊆ '''C''' halmaz belsején értjük azon pontok halmazát, melyeknek egy egész gömbi környezete benne van ''A''-ban | ||
| + | :<math>\mathrm{int}(A)=\{z\in \mathbf{C}\mid \exists r>0\quad \mathrm{B}_r(z)\subseteq A\}</math> | ||
| + | |||
| + | ===Folytonosság=== | ||
| + | |||
| + | Azt mondjuk, hogy az ''A'' ⊆ '''C''' halmazon értelmezett ''f'' függvény folytonos a ''z'' ∈ '''A''' pontban, ha ''z''-ben ''f'' folytonos mint '''R'''<sup>2</sup> ⊇ ''A'' <math>\to</math> '''R'''<sup>2</sup> függvény. Maga az ''f'' ''folytonos'', ha az értelmezési tartománya minden pontjában folytonos. | ||
| + | |||
| + | A többváltozós valós analízisből ismert tény miatt fennáll: | ||
| + | |||
| + | '''Állítás.''' Az ''f'' komplex függvény pontosan akkor folytonos az értelmezési tartománya egy pontjában, ha ott a függvény valós és képzetes része, mint kétváltozós valós függvény folytonos. Azaz, ha ''f''-et a következő alakban írjuk: | ||
| + | :<math>f(z)\equiv f(x,y)=u(x,y)+\mathrm{i}\cdot v(x,y)</math> | ||
| + | ahol ''u'' és ''v'' valós értékű függvények (rendre Re(''f'') és Im(''f'')), továbbá ''z''<sub>0</sub> = ''x''<sub>0</sub> + i''y''<sub>0</sub> ∈ Dom(''f''), akkor a következők ekvivalensek: | ||
| + | # ''f'' folytonos a ''z''<sub>0</sub>-ban | ||
| + | # ''u'' és ''v'' függvények folytonosak az (''x''<sub>0</sub>,''y''<sub>0</sub>)-ban | ||
| + | |||
| + | |||
| + | A kétváltozós függvények közötti határérték-folytonosság kapcsolat is megfogalmazható komplex módon. Itt az f = u + vi függvény határértékén a <math>z=x+iy</math> pontban a lim<sub>x</sub> u + i lim<sub>y</sub> v szám adja. Ekkor | ||
| + | |||
| + | |||
| + | '''Állítás.''' Az ''f'' komplex függvény pontosan akkor folytonos az értelmezési tartománya egy belső pontjában, ha ott a függvény létezik határértéke és az a helyettesítési érték. | ||
| + | : <math>\lim\limits_{z\to z_0} f(z)=f(z_0)</math> | ||
| + | |||
| + | |||
| + | '''Feladat.''' Legyen ''w'' ∈ '''C'''. Igazoljuk, hogy az alábbi függvények folytonosak! | ||
| + | # <math>z\mapsto w + z\,</math> | ||
| + | # <math>z\mapsto w\cdot z\,</math> | ||
| + | # <math>z\mapsto \overline{z}\,</math> | ||
| + | # <math>z\mapsto \frac{1}{z}\quad\quad (z\ne 0)</math> | ||
| + | |||
| + | ''Megoldás.'' | ||
| + | |||
| + | Az 1. az '''R'''<sup>2</sup>-ben eltolás a ''w''-nek megfelelő vektorral (Re(''w''), Im(''w''))-vel, így affin leképezés, ami folytonos. | ||
| + | |||
| + | 2. a ''w'' mátrixreprezentációjának megfelelő mátrixszal való szorzás, azaz lineáris leképezés, s így folytonos. | ||
| + | |||
| + | 3. azaz a konjugálás: (''x'',''y'') <math>\mapsto</math> (''x'',–''y'') a valós tengelyre való tükrözés, ami szintén lineáris. | ||
| + | |||
| + | Végül a reciprok: | ||
| + | :<math>\frac{1}{z}=\frac{\overline{z}}{z\overline{z}}=\frac{\overline{z}}{|z|^2}</math> | ||
| + | így, mint '''R'''<sup>2</sup> ⊃<math>\to</math> '''R'''<sup>2</sup> függvény: | ||
| + | :<math>\begin{pmatrix} | ||
| + | x \\ | ||
| + | y | ||
| + | \end{pmatrix}\mapsto | ||
| + | \begin{pmatrix} | ||
| + | \cfrac{x}{x^2+y^2} \\ | ||
| + | \cfrac{-y}{x^2+y^2} | ||
| + | \end{pmatrix}</math> | ||
| + | amely olyan, hogy mindkét komponensfüggvénye folytonos valós függvényekből van összeállítva a folytonosságot megőrző módon, azaz az értelmezési tartománya minden pontjában folytonos. | ||
| + | |||
| + | '''Feladat.''' Folytonos-e a ''z'' = 0-ban az | ||
| + | :<math>f(z)=\left\{ | ||
| + | \begin{matrix} | ||
| + | \cfrac{\mathrm{Im}(z)^3+\mathrm{i}\cdot\mathrm{Re}(z)^4}{\overline{z}\cdot z},\quad\quad\mathrm{ha}\;z\ne 0\\ | ||
| + | \\ | ||
| + | 0,\quad\quad \mathrm{ha}\;z=0 | ||
| + | \end{matrix} | ||
| + | \right.</math> | ||
| + | |||
| + | ''Megoldás.'' | ||
| + | |||
| + | Ha ''z'' = ''x'' + i''y'' és (''x'',''y'') ≠ (0,0), akkor: | ||
| + | :<math>f(x,y)=\begin{pmatrix} | ||
| + | \cfrac{y^3}{x^2+y^2} \\ | ||
| + | \cfrac{x^4}{x^2+y^2} | ||
| + | \end{pmatrix}</math> | ||
| + | |||
| + | A komponensfüggvények felírhatók egy 0-hoz tartó és egy korlátos függvény szorzataként: | ||
| + | :<math>\left|\cfrac{y^3}{x^2+y^2}\right|=|y|\cdot\frac{y^2}{x^2+y^2}\leq |y|\cdot\frac{y^2}{y^2}=|y|</math> | ||
| + | és | ||
| + | :<math>\left|\cfrac{x^4}{x^2+y^2}\right|=x^2\cdot\frac{x^2}{x^2+y^2}\leq x^2\cdot\frac{x^2}{x^2}=x^2</math> | ||
| + | így (x,y)<math>\to</math>(0,0) esetén a 0-hoz tartanak, így a függvény maga a (0,0)-hoz, azaz a komplex 0-hoz. Mivel itt a függvény értéke 0, ezért ''f'' a 0-ban folytonos. | ||
| + | |||
| + | |||
| + | Ha folytonos komplex függvényekből alapműveletek segítségével alkottunk függvényeket, akkor azok is folytonosak maradnak, mert a megfelelő '''R'''<sup>2</sup>-beli függvények ekkor olyanok lesznek, melyek mindegyik komponensfüggvénye a valós alapműveletek segítségével vannak definiálva. Ám, ezek megőrzik a folytonosságot. | ||
| + | |||
| + | '''Állítás.''' Ha ''f'' és ''g'' komplex függvények és az ''z''<sub>0</sub> pontban (mindketten értelmezettek és) folytonosak, akkor | ||
| + | # ''f'' + ''g'' | ||
| + | # ''f'' <math>\cdot</math> ''g'' | ||
| + | # <math>\overline{f}</math> | ||
| + | # ''g''(''z''<sub>0</sub>) ≠ 0 esetén ''f''/''g'' | ||
| + | is folytonos ''z''<sub>0</sub>-ban. | ||
| + | |||
| + | |||
| + | Folytonos függvények kompozíciója is folytonos (az kompozíció értelmezési tartományán). | ||
| + | |||
==Komplex számkör unicitása és reprezentációi== | ==Komplex számkör unicitása és reprezentációi== | ||
'''C''', azaz a komplex számok teste kétdimenziós valós vektortér. '''C''' elemei reprezentálhatók az '''R'''<sup>2</sup> síkon, a következő megfeleltetésekkel: | '''C''', azaz a komplex számok teste kétdimenziós valós vektortér. '''C''' elemei reprezentálhatók az '''R'''<sup>2</sup> síkon, a következő megfeleltetésekkel: | ||
| 49. sor: | 188. sor: | ||
:<math>w+B_r(z_0)=B_r(w+z_0)\,</math> | :<math>w+B_r(z_0)=B_r(w+z_0)\,</math> | ||
:<math>w\cdot B_r(z_0)\subseteq B_{r\cdot|w|}(wz_0)</math> | :<math>w\cdot B_r(z_0)\subseteq B_{r\cdot|w|}(wz_0)</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
A lap 2010. szeptember 15., 08:57-kori változata
Tartalomjegyzék |
Komplex számkör és reprezentációi
A komplex számok C halmazát és műveleteit legalább három, lényegesen más szemszögből lehet láttatni. A meghatározottság kedvéért összefoglaljuk a komplex számok legfontosabb algebrai tulajdonságait. Nem térünk ki minden egyes műveleti tulajdonságra, ezek megtalálhatók a komplex számok algebráját leíró tankönyvekben.
Algebrai modell
A komplex számok olyan
alakú formális kifejezések, ahol a és b valós számok, i pedig azzal a speciális tulajdonsággal rendelkezik, hogy
A komplex számok halmazát a C szimbólummal jelöljük. Akárcsak a legfeljebb elsőfokú a + bx alakú polinomok esetén, a C-t alkotó formális kifejezések között is értelmezhetjük az összeadást és a szorzást. Ezeket pontosan úgy definiáljuk, mint az a + bx alakú polinomok összegét és szorzatát, azzal a specialitással, hogy ahol a polinomok a szorzást követően másodfokúvá válnak, ott a komplex számok az i2=-1 egyenlőség miatt visszaérkeznek az a + bi alakú kifejezések körébe. Ezért lesz C zárt arra a szorzásra, amit a polinomok mintájára definiálunk.
Már innen is látszik, hogy a komplex számok halmaza kétdimenziós valós test feletti vektortér. Kimondhatjuk tehát:
Állítás. A C számkör a komplex számok
kétdimenziós valós vektorteret alkotnak és így lineárisan izomorfak a valós számpárok R2 vektorterével. |
Halmazelméleti modell
Az algebrai modellben nem teljesen világos, hogy mi is az i elem. Az előző állítás azonban lehetőséget biztosít arra, hogy konkrétan megadjuk a komplex számok halmazát mindenféle olyan kifejezés használata nélkül, mint "formális kifejezés" stb. (Valójában persze az algebrai modell is jól értelmezett módon adja meg a komplex számok halmazát, ha az a + bi alakú formális kifejezéseken az R[X] polinomgyűrűnek az (1+X2) polinommal történő maradékos osztásának maradékait értjük).
A számpár reprezentációban:
az összeadás az R2-beli vektorösszeadás, a szorzás, pedig a
művelet, mely természetesen a "polinomszorzásnak" az előző állításbeli izomorfizmus által létesített képe.
Ez az interpretáció azért fontos, mert explicitté teszi, hogy a C örökli az R2 topológiáját.
Geometriai modell
A szorzással együtt C egységelemes, nullosztómentes algebrát alkot (tehát vektortér és van egy mindkét változójában lineáris belső szorzás, melyben van egység és „nullával nem lehet osztani”). Felmerülhet a gyanúnk, hogy talán reprezentálhatjuk a komplex számokat a 2×2-es valós mátrixon M2×2 (R) algebrájának egy részalgebrájaként. Ezt a komplex számok trigonometrikus alakja segítségével tehetjük meg. Ismert, hogy a komplex számmal való szorzás forgatva nyújtás, azaz lineáris leképezés az R2 síkon:
Világos, hogy ekkor az a + bi kanonikus alakot használva a komplex számoknak megfelelő mátrixok halmaza:
Ez a mátrixhalmaz kétdimenziós altér az M2×2 (R) algebrában, melyet például a közvetve onnan is láthatjuk, hogy forgatva nyújtások is alteret alkotnak a lineáris leképezések terében.
C topológiája
R2 gömbi környezetei lesznek C gömbi környezetei. Általában, minden topologikus fogalom C-ben R2-re vezetünk vissza. Tehát, adott r > 0 valós számra és z0 ∈ C számra:
az r sugarú z0 középpontú nyílt gömbi környezet. Itt a | . | abszolútérték helyett, mely a || . ||2 euklideszi norma, elvileg R2 bármelyik normája alkalmas lenne, hisz véges dimenziós normált térben minden norma ekvivalens, azaz ugyanazokat a nyílt halmazokat határozzák meg. Szokásos módon értelmezettek az előbb említett nyílt halmazok is. Ω ⊆ C nyílt, ha minden pontjával együtt, annak egy nyílt gömbi környezetét is tartalmazza:
Egy A ⊆ C halmaz belsején értjük azon pontok halmazát, melyeknek egy egész gömbi környezete benne van A-ban
Folytonosság
Azt mondjuk, hogy az A ⊆ C halmazon értelmezett f függvény folytonos a z ∈ A pontban, ha z-ben f folytonos mint R2 ⊇ A  R2 függvény. Maga az f folytonos, ha az értelmezési tartománya minden pontjában folytonos.
R2 függvény. Maga az f folytonos, ha az értelmezési tartománya minden pontjában folytonos.
A többváltozós valós analízisből ismert tény miatt fennáll:
Állítás. Az f komplex függvény pontosan akkor folytonos az értelmezési tartománya egy pontjában, ha ott a függvény valós és képzetes része, mint kétváltozós valós függvény folytonos. Azaz, ha f-et a következő alakban írjuk:
ahol u és v valós értékű függvények (rendre Re(f) és Im(f)), továbbá z0 = x0 + iy0 ∈ Dom(f), akkor a következők ekvivalensek:
- f folytonos a z0-ban
- u és v függvények folytonosak az (x0,y0)-ban
A kétváltozós függvények közötti határérték-folytonosság kapcsolat is megfogalmazható komplex módon. Itt az f = u + vi függvény határértékén a z = x + iy pontban a limx u + i limy v szám adja. Ekkor
Állítás. Az f komplex függvény pontosan akkor folytonos az értelmezési tartománya egy belső pontjában, ha ott a függvény létezik határértéke és az a helyettesítési érték.
Feladat. Legyen w ∈ C. Igazoljuk, hogy az alábbi függvények folytonosak!
Megoldás.
Az 1. az R2-ben eltolás a w-nek megfelelő vektorral (Re(w), Im(w))-vel, így affin leképezés, ami folytonos.
2. a w mátrixreprezentációjának megfelelő mátrixszal való szorzás, azaz lineáris leképezés, s így folytonos.
3. azaz a konjugálás: (x,y)  (x,–y) a valós tengelyre való tükrözés, ami szintén lineáris.
(x,–y) a valós tengelyre való tükrözés, ami szintén lineáris.
Végül a reciprok:
így, mint R2 ⊃ R2 függvény:
R2 függvény:
amely olyan, hogy mindkét komponensfüggvénye folytonos valós függvényekből van összeállítva a folytonosságot megőrző módon, azaz az értelmezési tartománya minden pontjában folytonos.
Feladat. Folytonos-e a z = 0-ban az
Megoldás.
Ha z = x + iy és (x,y) ≠ (0,0), akkor:
A komponensfüggvények felírhatók egy 0-hoz tartó és egy korlátos függvény szorzataként:
és
így (x,y) (0,0) esetén a 0-hoz tartanak, így a függvény maga a (0,0)-hoz, azaz a komplex 0-hoz. Mivel itt a függvény értéke 0, ezért f a 0-ban folytonos.
(0,0) esetén a 0-hoz tartanak, így a függvény maga a (0,0)-hoz, azaz a komplex 0-hoz. Mivel itt a függvény értéke 0, ezért f a 0-ban folytonos.
Ha folytonos komplex függvényekből alapműveletek segítségével alkottunk függvényeket, akkor azok is folytonosak maradnak, mert a megfelelő R2-beli függvények ekkor olyanok lesznek, melyek mindegyik komponensfüggvénye a valós alapműveletek segítségével vannak definiálva. Ám, ezek megőrzik a folytonosságot.
Állítás. Ha f és g komplex függvények és az z0 pontban (mindketten értelmezettek és) folytonosak, akkor
- f + g
- f
 g
g
-
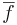
- g(z0) ≠ 0 esetén f/g
is folytonos z0-ban.
Folytonos függvények kompozíciója is folytonos (az kompozíció értelmezési tartományán).
Komplex számkör unicitása és reprezentációi
C, azaz a komplex számok teste kétdimenziós valós vektortér. C elemei reprezentálhatók az R2 síkon, a következő megfeleltetésekkel:
a vektortérműveletek pedig:
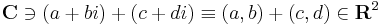 vektorösszeadás (a, b, c, d ∈ R)
vektorösszeadás (a, b, c, d ∈ R)
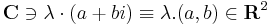 valós számmal való szorzás (λ, a, b ∈ R)
valós számmal való szorzás (λ, a, b ∈ R)
A komplex számok körét a komplex szorzás tulajdonságai egyértelműsítik. C nem csak kétdimenziós valós vektortér, de a szorzással algebra is, sőt C az egyetlen kétdimenziós kommutatív, nullosztómentes valós algebra -- izomorfizmus erejéig. Sok megjelenési formája lehet a komplex számoknak, de bármely két reprezentáció olyan, hogy található olyan kölcsönösen egyértelmű leképezés köztük, mely lineáris és megtartja a szorzást is (azaz algebra izomorfizmus).
A nullosztómentesség és a kommutativitás jellemzően a mátrixalgebrákban nemtriviális tulajdonság. A komplex számok olyan lineáris leképezéseknek felelnek meg, melyek mátrixa
A komplex számok szorzása itt a mátrixszorzás.
Ezek tényleg az R2 forgatva nyújtásai, csak át kell térnünk trigonometrikus alakra:
Topológia C-ben
C-ben, mint az R2 sík elemein tehát értelmezhetjük a gömbi környezeteket, mint az R2 sík pontjai körüli gömböket. Ezzel meg is kaptuk a C-beli nyílt halmazokat, azaz C topológiáját. A gömbök tehát a Gauss-számsík körlapjai:
ahol z ∈ C, r > 0 valós szám.
Világos, hogy akármilyen R2-beli norma szerinti gömböket is választhattunk volna a C gömbjeinek, mert R2-ben minden norma ugyanazt a topológiát származtatja. Mi a ||.||2-t, azaz az euklideszi normát emeltük ki.
Folytonosság
Egy f : C  C függvény folytonossága ezennel értelmezve van éspedig nem más, mint az R2-beli ||.||2 norma szerinti folytonosság. (HF: fogalmazzuk meg a C
C függvény folytonossága ezennel értelmezve van éspedig nem más, mint az R2-beli ||.||2 norma szerinti folytonosság. (HF: fogalmazzuk meg a C  C függvények folytonosságának epszilon-deltás definícióját!)
C függvények folytonosságának epszilon-deltás definícióját!)
Lineáris (jobban mondva R-lineáris), RN  RM függvény folytonos, így a műveltek folytonosak lesznek:
RM függvény folytonos, így a műveltek folytonosak lesznek:
és
folytonosak (az egyik az ||.||C,||.||C, a másik a ||.||C×C,||.||C normapárok szerint).
Mi több, a komplex számok legjellegzetesebb algebrai-topológiai tulajdonsága, hogy a komplex számok
szorzása is mindkét változójában R-lineáris, így folytonos.
Szemléletessé tehetjük a két fenti példát, ha a két művelet geometriai jelentését tekintjük. A hozzáadás eltolás, a komplex számmal szorzás forgatva nyújtás, így a gömbi környzeteket olyan alakzatokba képezik, melyek geometriai okokból mutatják a folytonosságot: