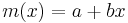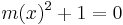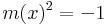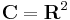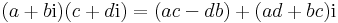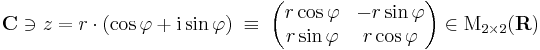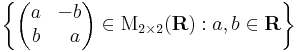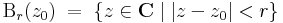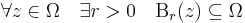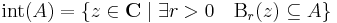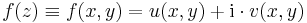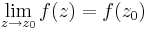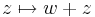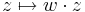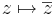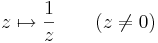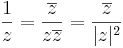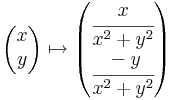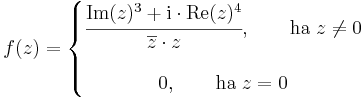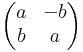Matematika A3a 2008/1. gyakorlat
Mozo (vitalap | szerkesztései) (→Differenciálegyenletek) |
Mozo (vitalap | szerkesztései) (→Differenciálegyenletek) |
||
| 11. sor: | 11. sor: | ||
Az egyenlet ''explicit általános megoldása'' (a ''H''⊆''I''×''J'' halmazon ) az ''y'':''K''×'''R'''<math>\to</math>''J'', y(x)=Ψ(x,C) függvény, ha minden (''H''-beli) kezdeti feltételhez egyértelműen létezik olyan ''C'', melyre y(x)=Ψ(x,C) megoldása az egyenletnek. | Az egyenlet ''explicit általános megoldása'' (a ''H''⊆''I''×''J'' halmazon ) az ''y'':''K''×'''R'''<math>\to</math>''J'', y(x)=Ψ(x,C) függvény, ha minden (''H''-beli) kezdeti feltételhez egyértelműen létezik olyan ''C'', melyre y(x)=Ψ(x,C) megoldása az egyenletnek. | ||
| − | A legegyszerűbb differenciálegyenlet az 'y'''=''f''(''x''), ami lényegében primitívfüggvénykeresés. Tudjuk, hogy (folytonos ''f'' esetén) mindig van ennek megoldása, éspedig az integrálfüggvény az, de ez nem feltétlenül kapható meg elemi függvények segítségével "kézzel fogható" zárt alakban. Általánosabb esetben a közönséges elsőrendű differenciálegyenletek megoldásának két általános, de természetesen ugyanígy (zárt megoldás szempontjából) nem mindig célra vezető módszere a ''szeparálás'' és az ''egzakt differenciálegyenlet'' módszere. | + | A legegyszerűbb differenciálegyenlet az ''y'''=''f''(''x''), ami lényegében primitívfüggvénykeresés. Tudjuk, hogy (folytonos ''f'' esetén) mindig van ennek megoldása, éspedig az integrálfüggvény az, de ez nem feltétlenül kapható meg elemi függvények segítségével "kézzel fogható" zárt alakban. Általánosabb esetben a közönséges elsőrendű differenciálegyenletek megoldásának két általános, de természetesen ugyanígy (zárt megoldás szempontjából) nem mindig célra vezető módszere a ''szeparálás'' és az ''egzakt differenciálegyenlet'' módszere. |
===Szeparábilis differenciálegyenlet=== | ===Szeparábilis differenciálegyenlet=== | ||
A lap 2013. augusztus 28., 20:53-kori változata
Tartalomjegyzék |
Differenciálegyenletek
Legyen F:I×J R korlátos és zárt téglalapon értelmezett folytonos kétváltozós függvény. Az
R korlátos és zárt téglalapon értelmezett folytonos kétváltozós függvény. Az
- y ' = F(x,y)
elsőrendű közönséges differenciálegyenlet megoldásainak nevezzük az olyan y:K J függvényeket, melyekre
J függvényeket, melyekre
- 1) K⊆I,
- 2) y differenciálható és
- 3) minden x ∈ K számra y'(x)=F(x,y(x)).
Ha (x0,y0)∈I×J, akkor az egyenlet y0 = y(x0) kezdeti feltételt kielégítő partikuláris megoldásának venezzük az olyan megoldásokat, melyekre y0 = y(x0). Adott kezdeti feltételt kielégítő megoldás keresését kezdeti érték problémának vagy Cauchy-problémának nevezzük. Az egyenlet összes megoldása az egyenlet összes megoldása.
Azt mondjuk, hogy az egyenlet általános megoldását (a H⊆I×J halmazon) az Φ(x,y,C)=0 implicit egyenlet szolgáltatja (vagy az egyenlet általános megoldása az előbbi implicit alakban adott), ha minden (H-beli) (x0,y0) kezdeti feltételre van egyetlen olyan C valós paraméter, hogy az Φ(x,y,C)=0 implicit egyenlet megoldása az egyenletnek az adott kezdeti feltételt kielégítő megoldása.
Az egyenlet explicit általános megoldása (a H⊆I×J halmazon ) az y:K×R J, y(x)=Ψ(x,C) függvény, ha minden (H-beli) kezdeti feltételhez egyértelműen létezik olyan C, melyre y(x)=Ψ(x,C) megoldása az egyenletnek.
J, y(x)=Ψ(x,C) függvény, ha minden (H-beli) kezdeti feltételhez egyértelműen létezik olyan C, melyre y(x)=Ψ(x,C) megoldása az egyenletnek.
A legegyszerűbb differenciálegyenlet az y'=f(x), ami lényegében primitívfüggvénykeresés. Tudjuk, hogy (folytonos f esetén) mindig van ennek megoldása, éspedig az integrálfüggvény az, de ez nem feltétlenül kapható meg elemi függvények segítségével "kézzel fogható" zárt alakban. Általánosabb esetben a közönséges elsőrendű differenciálegyenletek megoldásának két általános, de természetesen ugyanígy (zárt megoldás szempontjából) nem mindig célra vezető módszere a szeparálás és az egzakt differenciálegyenlet módszere.
Szeparábilis differenciálegyenlet
Komplex számkör és reprezentációi
A komplex számok C halmazát és műveleteit legalább három, lényegesen más szemszögből lehet láttatni. A meghatározottság kedvéért összefoglaljuk a komplex számok legfontosabb algebrai tulajdonságait. Nem térünk ki minden egyes műveleti tulajdonságra, ezek megtalálhatók a komplex számok algebráját leíró tankönyvekben.
Algebrai modell
A komplex számok olyan
alakú formális kifejezések, ahol a és b valós számok, i pedig azzal a speciális tulajdonsággal rendelkezik, hogy
A komplex számok halmazát a C szimbólummal jelöljük, tehát
itt a-t a z valós részének nevezzük és Re(z)-vel jelöljük, b-t a z képzetes részének nevezzük és Im(z)-vel jelöljük. Világos, hogy Im(z) ∈ R, azaz "tiszta" valós.
Megjegyzés. A kevéssé informatív "formális kifejezés" helyett bevezethetjük a komplex számokat valódi algebrai objektumokként. A komplex számok halmazát egy a maradékos osztással rendelkező halmazból konstrulájuk: a valós együtthatós polinomok R[X] halmazából. Közismert, hogy a valósegyütthatós, egyhatározatlanú polinomokal, azaz a
alakú kifejezésekkel, ahol az ai-k valós számok, n pedig nemnegatív egész, lehet maradékosan osztani (polinomosztás). Ekkor
azaz a komplex számok halmaza a valósegyütthatós polinomok x2+1 polinommal történő osztási maradékai. Világos, hogy minden ilyen maradék előáll
alakban, azaz legfeljebb elsőfokú polinom alakjában. Ebben a számkörben az összeadás a polinomösszeadás, a szorzás a polinomok szorzása (illetve ezen eredményének x2+1-vel történő osztási maradéka). Amikor két elsőfokú polinom szorzata másodfokú, akkor sem lépünk ki a számkörből, hisz a
polinomegyenlet megoldható, éspedig az m(x)=x polinom (az identitás) megoldás. Ekkor
azaz ebben a számkörben létezik a -1-nek négyzetgyöke. Az m(x)=x polinom az, mely az i egység szerepét játssza és így is jelöljük ezt ezentúl.
Akárcsak a legfeljebb elsőfokú a + bx alakú polinomok esetén, a C-t alkotó formális kifejezések között is értelmezhetjük az összeadást és a szorzást. Ezeket pontosan úgy definiáljuk, mint az a + bx alakú polinomok összegét és szorzatát, azzal a specialitással, hogy ahol a polinomok a szorzást követően másodfokúvá válnak, ott a komplex számok az i2=-1 egyenlőség miatt visszaérkeznek az a + bi alakú kifejezések körébe. Ezért lesz C zárt arra a szorzásra, amit a polinomok mintájára definiálunk.
Már innen is látszik, hogy a komplex számok halmaza kétdimenziós valós test feletti vektortér. Kimondhatjuk tehát:
Állítás. A C számkör a komplex számok
- (a+bi) + (c+di) = (a+c) + (b+d)i összeadásával és a
- λ(a+bi) = λa + λbi, a λ valós számmal való szorzással
kétdimenziós valós vektorteret alkotnak és így lineárisan izomorfak a valós számpárok R2 vektorterével.
Halmazelméleti modell
Az algebrai modellben nem teljesen világos, hogy mi is az i elem. Az előző állítás azonban lehetőséget biztosít arra, hogy konkrétan megadjuk a komplex számok halmazát mindenféle olyan kifejezés használata nélkül, mint "formális kifejezés" stb. (Valójában persze az algebrai modell is jól értelmezett módon adja meg a komplex számok halmazát, ha az a + bi alakú formális kifejezéseken az R[X] polinomgyűrűnek az (1+X2) polinommal történő maradékos osztásának maradékait értjük).
A számpár reprezentációban:
az összeadás az R2-beli vektorösszeadás, a szorzás, pedig a
művelet, mely természetesen a "polinomszorzásnak" az előző állításbeli izomorfizmus által létesített képe.
Ez az interpretáció azért fontos, mert explicitté teszi, hogy a C örökli az R2 topológiáját.
Geometriai modell
A szorzással együtt C egységelemes, nullosztómentes algebrát alkot (tehát vektortér és van egy mindkét változójában lineáris belső szorzás, melyben van egység és „nullával nem lehet osztani”). Felmerülhet a gyanúnk, hogy talán reprezentálhatjuk a komplex számokat a 2×2-es valós mátrixon M2×2 (R) algebrájának egy részalgebrájaként. Ezt a komplex számok trigonometrikus alakja segítségével tehetjük meg. Ismert, hogy a komplex számmal való szorzás forgatva nyújtás, azaz lineáris leképezés az R2 síkon:
Világos, hogy ekkor az a + bi kanonikus alakot használva a komplex számoknak megfelelő mátrixok halmaza:
Ez a mátrixhalmaz kétdimenziós altér az M2×2 (R) algebrában, melyet például a közvetve onnan is láthatjuk, hogy forgatva nyújtások is alteret alkotnak a lineáris leképezések terében.
C topológiája
R2 gömbi környezetei lesznek C gömbi környezetei. Általában, minden topologikus fogalom C-ben R2-re vezetünk vissza. Tehát, adott r > 0 valós számra és z0 ∈ C számra:
az r sugarú z0 középpontú nyílt gömbi környezet. Itt a | . | abszolútérték helyett, mely a || . ||2 euklideszi norma, elvileg R2 bármelyik normája alkalmas lenne, hisz véges dimenziós normált térben minden norma ekvivalens, azaz ugyanazokat a nyílt halmazokat határozzák meg. Szokásos módon értelmezettek az előbb említett nyílt halmazok is. Ω ⊆ C nyílt, ha minden pontjával együtt, annak egy nyílt gömbi környezetét is tartalmazza:
Egy A ⊆ C halmaz belsején értjük azon pontok halmazát, melyeknek egy egész gömbi környezete benne van A-ban
Mivel R2-ben minden norma ekvivalens (ugyanazokat a nyílt halmazokat határozzák meg), ezért adott feladatokban tetszőleges, a feladathoz jól illeszkedő normát választhatunk. Topologikus szempontokból a komplex és R2-R2 függvények között a következő azonosítással élhetünk. Ha f: C⊇  C függvény, akkor z = x + iy, f(z)=u(x,y)+iv(x,y), ill.
C függvény, akkor z = x + iy, f(z)=u(x,y)+iv(x,y), ill.
Folytonosság
Azt mondjuk, hogy az A ⊆ C halmazon értelmezett f függvény folytonos a z ∈ A pontban, ha z-ben f folytonos mint R2 ⊇ A  R2 függvény. Maga az f folytonos, ha az értelmezési tartománya minden pontjában folytonos.
R2 függvény. Maga az f folytonos, ha az értelmezési tartománya minden pontjában folytonos.
A többváltozós valós analízisből ismert tény miatt fennáll:
Állítás. Az f komplex függvény pontosan akkor folytonos az értelmezési tartománya egy pontjában, ha ott a függvény valós és képzetes része, mint kétváltozós valós függvény folytonos. Azaz, ha f-et a következő alakban írjuk:
ahol u és v valós értékű függvények (rendre Re(f) és Im(f)), továbbá z0 = x0 + iy0 ∈ Dom(f), akkor a következők ekvivalensek:
- f folytonos a z0-ban
- u és v függvények folytonosak az (x0,y0)-ban
A kétváltozós függvények közötti határérték-folytonosság kapcsolat is megfogalmazható komplex módon. Itt az f = u + vi függvény határértékén a z = x + iy pontban a limx u + i limy v szám adja. Ekkor
Állítás. Az f komplex függvény pontosan akkor folytonos az értelmezési tartománya egy belső pontjában, ha ott a függvénynek létezik határértéke és az a helyettesítési érték.
A komplex függvények folytonosságának egyik, de nem egyetlen feltétele az, hogy az (u,v) reprezentáció R2-ben lineáris legyen, hiszen a véges dimenziós normált terek között ható lineáris leképezések folytonosak. A nem-folytonosságnál érdemes a határérték nem létezését vizsgálni, hátha ez célra vezet.
Feladat. Legyen w ∈ C. Igazoljuk, hogy az alábbi függvények folytonosak!
Megoldás.
Az 1. az R2-ben eltolás a w-nek megfelelő vektorral (Re(w), Im(w))-vel, így affin leképezés, ami folytonos.
2. a w mátrixreprezentációjának megfelelő mátrixszal való szorzás, azaz lineáris leképezés, s így folytonos.
3. azaz a konjugálás: (x,y)  (x,–y) a valós tengelyre való tükrözés, ami szintén lineáris.
(x,–y) a valós tengelyre való tükrözés, ami szintén lineáris.
Végül a reciprok:
így, mint R2 ⊃ R2 függvény:
R2 függvény:
amely olyan, hogy mindkét komponensfüggvénye folytonos valós függvényekből van összeállítva a folytonosságot megőrző módon, azaz az értelmezési tartománya minden pontjában folytonos.
Feladat. Folytonos-e a z = 0-ban az
Megoldás.
Ha z = x + iy és (x,y) ≠ (0,0), akkor:
A komponensfüggvények felírhatók egy 0-hoz tartó és egy korlátos függvény szorzataként:
és
így (x,y) (0,0) esetén a 0-hoz tartanak, így a függvény maga a (0,0)-hoz, azaz a komplex 0-hoz. Mivel itt a függvény értéke 0, ezért f a 0-ban folytonos.
(0,0) esetén a 0-hoz tartanak, így a függvény maga a (0,0)-hoz, azaz a komplex 0-hoz. Mivel itt a függvény értéke 0, ezért f a 0-ban folytonos.
Ha folytonos komplex függvényekből alapműveletek segítségével alkottunk függvényeket, akkor azok is folytonosak maradnak, mert a megfelelő R2-beli függvények ekkor olyanok lesznek, melyek mindegyik komponensfüggvénye a valós alapműveletek segítségével vannak definiálva. Ám, ezek megőrzik a folytonosságot.
Állítás. Ha f és g komplex függvények és az z0 pontban (mindketten értelmezettek és) folytonosak, akkor
- f + g
- f
 g
g
-
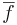
- g(z0) ≠ 0 esetén f/g
is folytonos z0-ban.
Folytonos függvények kompozíciója is folytonos (az kompozíció értelmezési tartományán).
Komplex számkör unicitása
C, azaz a komplex számok teste kétdimenziós valós vektortér. C elemei reprezentálhatók az R2 síkon, a következő megfeleltetésekkel:
a vektortérműveletek pedig:
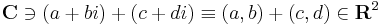 vektorösszeadás (a, b, c, d ∈ R)
vektorösszeadás (a, b, c, d ∈ R)
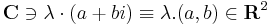 valós számmal való szorzás (λ, a, b ∈ R)
valós számmal való szorzás (λ, a, b ∈ R)
A komplex számok körét a komplex szorzás tulajdonságai egyértelműsítik. C nem csak kétdimenziós valós vektortér, de a szorzással algebra is, sőt C az egyetlen kétdimenziós kommutatív, nullosztómentes valós algebra -- izomorfizmus erejéig. Sok megjelenési formája lehet a komplex számoknak, de bármely két reprezentáció olyan, hogy található olyan kölcsönösen egyértelmű leképezés köztük, mely lineáris és megtartja a szorzást is (azaz algebra izomorfizmus).
A nullosztómentesség és a kommutativitás jellemzően a mátrixalgebrákban nemtriviális tulajdonság. A komplex számok olyan lineáris leképezéseknek felelnek meg, melyek mátrixa
A komplex számok szorzása itt a mátrixszorzás.
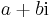
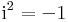
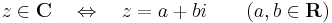
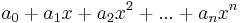
![\mathbf{C}=_{\mathrm{def}}\mathbf{R}[X]/(x^2+1)](/upload/math/d/3/6/d361c86f4c4cc3f09273ef5ab65b6197.png)