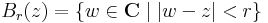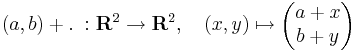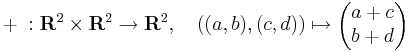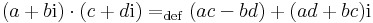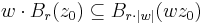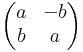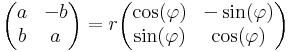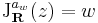Matematika A3a 2008/1. gyakorlat

Topológia C-ben

C, azaz a komplex számok teste kétdimenziós valós vektortér. C elemei reprezentálhatók az R² síkon, a következő megfeleltetésekkel:

$\mathbf{C}\ni a+bi\equiv (a,b)\in \mathbf{R}^2$

a vektortérműveletek pedig:

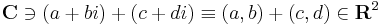$\mathbf{C}\ni (a+bi)+(c+di)\equiv (a,b)+(c,d)\in \mathbf{R}^2$ vektorösszeadás (a, b, c, d ∈ R)

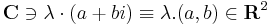$\mathbf{C}\ni \lambda\cdot(a+bi)\equiv \lambda.(a,b)\in \mathbf{R}^2$ valós számmal való szorzás (λ, a, b ∈ R)

C-ben tehát értelmezhetjük a gömbi környezeteket, mint az R² sík pontjai körüli gömböket. Ezzel meg is kaptuk a C-beli nyílt halmazokat, azaz C topológiáját. A gömbök tehát a Gauss-számsík körlapjai:

$B_r(z)=\{w\in \mathbf{C}\mid |w-z|< r\}$

ahol z ∈ C, r > 0 valós szám.

Világos, hogy akármilyen R²-beli norma szerinti gömböket is választhattunk volna a C gömbjeinek, mert R²-ben minden norma ugyanazt a topológiát származtatja. Mi a ||.||₂-t, azaz az euklideszi normát emeltük ki.

Folytonosság

Egy f : C $\to$ C függvény folytonossága ezennel értelmezve van éspedig nem más, mint az R²-beli ||.||₂ norma szerinti folytonosság. (HF: fogalmazzuk meg a C $\to$ C függvények folytonosságának epszilon-deltás definícióját!)

Lineáris (jobban mondva R-lineáris), R^N $\to$ R^M függvény folytonos, így a műveltek folytonosak lesznek:

$(a,b)+.\;:\mathbf{R}^2\to\mathbf{R}^2,\quad(x,y)\mapsto\begin{pmatrix}a + x\\b + y\end{pmatrix}$

és

$+\;:\mathbf{R}^2\times\mathbf{R}^2\to\mathbf{R}^2,\quad((a,b),(c,d))\mapsto\begin{pmatrix}a + c\\b + d\end{pmatrix}$

folytonosak (az egyik az ||.||_C,||.||_C, a másik a ||.||_C×C,||.||_C normapárok szerint).

Mi több, a komplex számok legjellegzetesebb algebrai-topológiai tulajdonsága, hogy a komplex számok

$(a+b\mathrm{i})\cdot (c+d\mathrm{i})=_{\mathrm{def}}(ac-bd)+(ad+bc)\mathrm{i}$

szorzása is mindkét változójában R-lineáris, így folytonos.

Szemléletessé tehetjük a két fenti példát, ha a két művelet geometriai jelentését tekintjük. A hozzáadás eltolás, a komplex számmal szorzás forgatva nyújtás, így a gömbi környzeteket olyan alakzatokba képezik, melyek geometriai okokból mutatják a folytonosságot:

$w+B_r(z_0)=B_r(w+z_0)\,$

$w\cdot B_r(z_0)\subseteq B_{r\cdot|w|}(wz_0)$

Komplex számkör unicitása és mátrixreprezentációja

A komplex számok körét a komplex szorzás tulajdonságai egyértelműsítik. C nem csak kétdimenziós valós vektortér, de a szorzással algebra is, sőt C az egyetlen kétdimenziós kommutatív, nullosztómentes valós algebra -- izomorfizmus erejéig. Sok megjelenési formája lehet a komplex számoknak, de bármely két reprezentáció olyan, hogy található olyan kölcsönösen egyértelmű leképezés köztük, mely lineáris és megtartja a szorzást is (azaz algebra izomorfizmus).

A nullosztómentesség és a kommutativitás jellemzően a mátrixalgebrákban nemtriviális tulajdonság. A komplex számok olyan lineáris leképezéseknek felelnek meg, melyek mátrixa

$\begin{pmatrix} a & -b\\ b & a \end{pmatrix}$

A komplex számok szorzása itt a mátrixszorzás.

Ezek tényleg az R² forgatva nyújtásai, csak át kell térnünk trigonometrikus alakra:

$\begin{pmatrix} a & -b\\ b & a \end{pmatrix}=r\begin{pmatrix} \cos(\varphi) & -\sin(\varphi)\\ \sin(\varphi) & \cos(\varphi) \end{pmatrix}$

R-differenciálhatóság

Egy f : C $\to$ C függvény abban az értelemen R-differenciálható, ahogy egy R^N $\to$ R^M függvény differenciálhatóságát definiáltuk. Ekkor például a hozzáadás, mint affin függvény R-differenciálható, és R-differenciálja az identitás:

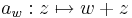$a_w:z\mapsto w+ z\,$ akkor $\mathrm{d}_\mathbf{R}(a_w)z=z$

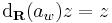
A komplex számmal szorzás R-differenciálját közvetlenül a definíciójából számíthatjuk ki:

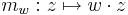$m_w:z\mapsto w\cdot z\,$ akkor $\mathrm{J}_\mathbf{R}^{a_w}(z)=\begin{pmatrix} w_1 & -w_2\\ w_2 & w_1 \end{pmatrix}$

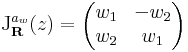
Rendkívül érdekes észrevétel tanúi lehetünk ekkor. z $\mapsto$ w$\cdot$ z R-deriváltja maga w komplex számnak megfelelő mátrix, azaz

$\mathrm{J}_\mathbf{R}^{a_w}(z)=w$

ha mátrixreprezentációt veszünk. Sőt, visszanézve ez az összeadásra is igaz:

$\mathrm{J}_\mathbf{R}^{a_w}(z)=\begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}$