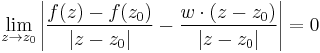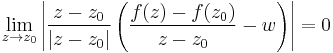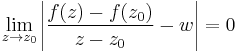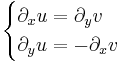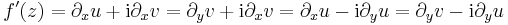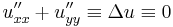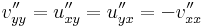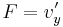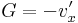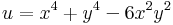Matematika A3a 2008/7. gyakorlat
Mozo (vitalap | szerkesztései) (→Cirkulációmentesség) |
Mozo (vitalap | szerkesztései) |
||
| (egy szerkesztő 4 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | ''<sub><[[Matematika A3a 2008]]</sub>'' | + | ''<sub><[[Matematika A3a 2008]]</sub>'' |
| − | == | + | ==Folytonosság== |
| − | + | Azt mondjuk, hogy az ''A'' ⊆ '''C''' halmazon értelmezett ''f'' függvény folytonos a ''z'' ∈ '''A''' pontban, ha ''z''-ben ''f'' folytonos mint '''R'''<sup>2</sup> ⊇ ''A'' <math>\to</math> '''R'''<sup>2</sup> függvény. Maga az ''f'' ''folytonos'', ha az értelmezési tartománya minden pontjában folytonos. | |
| − | + | A többváltozós valós analízisből ismert tény miatt fennáll: | |
| − | : | + | |
| − | + | ||
| − | + | '''Állítás.''' Az ''f'' komplex függvény pontosan akkor folytonos az értelmezési tartománya egy pontjában, ha ott a függvény valós és képzetes része, mint kétváltozós valós függvény folytonos. Azaz, ha ''f''-et a következő alakban írjuk: | |
| + | :<math>f(z)\equiv f(x,y)=u(x,y)+\mathrm{i}\cdot v(x,y)</math> | ||
| + | ahol ''u'' és ''v'' valós értékű függvények (rendre Re(''f'') és Im(''f'')), továbbá ''z''<sub>0</sub> = ''x''<sub>0</sub> + i''y''<sub>0</sub> ∈ Dom(''f''), akkor a következők ekvivalensek: | ||
| + | # ''f'' folytonos a ''z''<sub>0</sub>-ban | ||
| + | # ''u'' és ''v'' függvények folytonosak az (''x''<sub>0</sub>,''y''<sub>0</sub>)-ban | ||
| − | == | + | ==Határérték== |
| − | ''' | + | Komplex függvény '''C'''-beli pontban vett '''C'''-beli határértéke ugyanúgy értelmezett, mint az '''R'''<sup>2</sup> esetben. Itt is érvényes, hogy pontosan akkor látezik a határérték, ha a komponensfüggvényeknek létezik a határértéke és ekkor a határérték egyenlő lesz a valós és képzetes komponens határértékéből alkotott komplex számmal. |
| − | + | A ∞ miatt érdemes külön is megfogalmazni a határérték definícióját, bár az teljesen analóg a valós esettel. Legyen ''f'' egy az ''A'' ⊆ '''C''' halmazon értelmezett, '''C'''-be képező függvény. Legyen <math>\scriptstyle{u\in \overline{\mathbf{C}}}</math> az ''A'' torlódási pontja, azaz minden ''r'' > 0 esetén legyen olyan ''a'' ∈ ''A'', hogy ''a'' ∈ B<sub>r</sub>(''u'')\{u}. Azt mondjuk, hogy az ''f''-nek a <math>\scriptstyle{v\in \overline{\mathbf{C}}}</math> elem határértéke az ''u''-ban, ha | |
| − | + | :minden ε > 0 esetén létezik olyan δ > 0, hogy minden ''z'' ∈ ''A'' ∩ B<sub>δ</sub>(''u'')\{u}-re ''f''(''z'') ∈ B<sub>ε</sub>(''v'') | |
| − | ''' | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | : | + | |
| − | + | ahol természetesen a ∞ környezetei a már említett módon értendők. | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | A kétváltozós függvények közötti határérték-folytonosság kapcsolat is megfogalmazható komplex módon. Itt az f = u + vi függvény határértékén a <math>z=x+iy</math> pontban a lim<sub>x</sub> u + i lim<sub>y</sub> v szám adja. Ekkor | ||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''Állítás.''' Az ''f'' komplex függvény pontosan akkor folytonos az értelmezési tartománya egy belső pontjában, ha ott a függvénynek létezik határértéke és az a helyettesítési érték. |
| + | : <math>\lim\limits_{z\to z_0} f(z)=f(z_0)</math> | ||
| + | A komplex függvények folytonosságának egyik, de nem egyetlen feltétele az, hogy az (u,v) reprezentáció '''R'''<sup>2</sup>-ben lineáris legyen, hiszen ''a véges dimenziós normált terek között ható lineáris leképezések folytonosak.'' A nem-folytonosságnál érdemes a határérték nem létezését vizsgálni, hátha ez célra vezet. | ||
| − | |||
| − | |||
| − | |||
| − | === | + | ==Feladat folytonosságra== |
| − | + | ||
| − | + | ||
| − | + | ||
| − | ''' | + | '''Feladat.''' Legyen ''w'' ∈ '''C'''. Igazoljuk, hogy az alábbi függvények folytonosak! |
| − | + | # <math>z\mapsto w + z\,</math> | |
| + | # <math>z\mapsto w\cdot z\,</math> | ||
| + | # <math>z\mapsto \overline{z}\,</math> | ||
| + | # <math>z\mapsto \frac{1}{z}\quad\quad (z\ne 0)</math> | ||
| − | '' | + | ''Megoldás.'' |
| − | + | ||
| − | + | Az 1. az '''R'''<sup>2</sup>-ben eltolás a ''w''-nek megfelelő vektorral (Re(''w''), Im(''w''))-vel, így affin leképezés, ami folytonos. | |
| − | + | ||
| − | + | 2. a ''w'' mátrixreprezentációjának megfelelő mátrixszal való szorzás, azaz lineáris leképezés, s így folytonos. | |
| − | + | ||
| − | ( | + | 3. azaz a konjugálás: (''x'',''y'') <math>\mapsto</math> (''x'',–''y'') a valós tengelyre való tükrözés, ami szintén lineáris. |
| − | + | Végül a reciprok: | |
| − | + | :<math>\frac{1}{z}=\frac{\overline{z}}{z\overline{z}}=\frac{\overline{z}}{|z|^2}</math> | |
| − | + | így, mint '''R'''<sup>2</sup> ⊃<math>\to</math> '''R'''<sup>2</sup> függvény: | |
| − | :<math>\ | + | :<math>\begin{pmatrix} |
| − | + | x \\ | |
| + | y | ||
| + | \end{pmatrix}\mapsto | ||
| + | \begin{pmatrix} | ||
| + | \cfrac{x}{x^2+y^2} \\ | ||
| + | \cfrac{-y}{x^2+y^2} | ||
| + | \end{pmatrix}</math> | ||
| + | amely olyan, hogy mindkét komponensfüggvénye folytonos valós függvényekből van összeállítva a folytonosságot megőrző módon, azaz az értelmezési tartománya minden pontjában folytonos. | ||
| − | '' | + | '''Feladat.''' Folytonos-e a ''z'' = 0-ban az |
| − | :<math>\ | + | :<math>f(z)=\left\{ |
| − | + | \begin{matrix} | |
| + | \cfrac{\mathrm{Im}(z)^3+\mathrm{i}\cdot\mathrm{Re}(z)^4}{\overline{z}\cdot z},\quad\quad\mathrm{ha}\;z\ne 0\\ | ||
| + | \\ | ||
| + | 0,\quad\quad \mathrm{ha}\;z=0 | ||
| + | \end{matrix} | ||
| + | \right.</math> | ||
| − | + | ''Megoldás.'' | |
| − | :<math>=\ | + | |
| + | Ha ''z'' = ''x'' + i''y'' és (''x'',''y'') ≠ (0,0), akkor: | ||
| + | :<math>f(x,y)=\begin{pmatrix} | ||
| + | \cfrac{y^3}{x^2+y^2} \\ | ||
| + | \cfrac{x^4}{x^2+y^2} | ||
| + | \end{pmatrix}</math> | ||
| − | :<math> | + | A komponensfüggvények felírhatók egy 0-hoz tartó és egy korlátos függvény szorzataként: |
| − | + | :<math>\left|\cfrac{y^3}{x^2+y^2}\right|=|y|\cdot\frac{y^2}{x^2+y^2}\leq |y|\cdot\frac{y^2}{y^2}=|y|</math> | |
| − | :<math> | + | és |
| − | + | :<math>\left|\cfrac{x^4}{x^2+y^2}\right|=x^2\cdot\frac{x^2}{x^2+y^2}\leq x^2\cdot\frac{x^2}{x^2}=x^2</math> | |
| − | + | így (x,y)<math>\to</math>(0,0) esetén a 0-hoz tartanak, így a függvény maga a (0,0)-hoz, azaz a komplex 0-hoz. Mivel itt a függvény értéke 0, ezért ''f'' a 0-ban folytonos. | |
| − | |||
| − | + | Ha folytonos komplex függvényekből alapműveletek segítségével alkottunk függvényeket, akkor azok is folytonosak maradnak, mert a megfelelő '''R'''<sup>2</sup>-beli függvények ekkor olyanok lesznek, melyek mindegyik komponensfüggvénye a valós alapműveletek segítségével vannak definiálva. Ám, ezek megőrzik a folytonosságot. | |
| − | ''' | + | '''Állítás.''' Ha ''f'' és ''g'' komplex függvények és az ''z''<sub>0</sub> pontban (mindketten értelmezettek és) folytonosak, akkor |
| − | + | # ''f'' + ''g'' | |
| + | # ''f'' <math>\cdot</math> ''g'' | ||
| + | # <math>\overline{f}</math> | ||
| + | # ''g''(''z''<sub>0</sub>) ≠ 0 esetén ''f''/''g'' | ||
| + | is folytonos ''z''<sub>0</sub>-ban. | ||
| − | |||
| − | + | Folytonos függvények kompozíciója is folytonos (az kompozíció értelmezési tartományán). | |
| − | = | + | '''Feladat.''' Folytonos-e a ''z'' = i-ben az |
| − | + | :<math>f(z)=\left\{ | |
| + | \begin{matrix} | ||
| + | \cfrac{\mathrm{i}z+1}{|z-\mathrm{i}|},\quad\quad\mathrm{ha}\;z\ne \mathrm{i}\\ | ||
| + | \\ | ||
| + | 0,\quad\quad \mathrm{ha}\;z=\mathrm{i} | ||
| + | \end{matrix} | ||
| + | \right.</math> | ||
| − | ''' | + | Ha ''z'' = ''x'' + i''y'' és (''x'',''y'') ≠ (0,1), akkor: |
| − | :<math>\ | + | :<math>f(x,y)=\begin{pmatrix} |
| + | \cfrac{-y+1}{\sqrt{x^2+(y-1)^2}} \\ | ||
| + | \cfrac{x}{\sqrt{x^2+(y-1)^2}} | ||
| + | \end{pmatrix}</math> | ||
| − | + | Már az első komponens határértéke sem létezik, hisz (x,y)=(0,y) mentén alulról a (0,1)-hez tartva a határérték -1, az x=y-1 mentén pedig -1/gyök kettő. | |
| − | + | A második tényező szintén nem. | |
| − | + | ==Feladatok határértékre== | |
| − | + | '''Feladat.''' Igazoljuk definíció szerint, hogy | |
| − | :<math> | + | #<math>\lim\limits_{z\to 0}\frac{1}{z}=\infty</math> |
| − | + | #<math>\lim\limits_{z\to \infty}\frac{1}{z}=0</math> | |
| + | |||
| + | 1. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |''z''| < δ esetén, hogy a függvényérték a ∞ ε sugarú környezetébe esik, azaz: | ||
| + | :<math>\left|\frac{1}{z}\right|>\frac{1}{\varepsilon}</math> | ||
| + | Világos, hogy ezt azt jelenti, hogy | ||
| + | :<math>|z|<\varepsilon</math> | ||
| + | amit reciprokvonással kaptunk. Ha tehát ha δ := ε és |''z''| < δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség. | ||
| − | + | 2. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |''z''| > 1/δ esetén, hogy a függvényérték a 0-nak ε sugarú környezetébe esik, azaz: | |
| − | :<math>\ | + | :<math>\left|\frac{1}{z}\right|<\varepsilon</math> |
| − | + | Világos, hogy ezt azt jelenti, hogy | |
| + | :<math>|z|>\frac{1}{\varepsilon}</math> | ||
| + | amit reciprokvonással kaptunk. Ha tehát ha δ := ε és |''z''| > 1/δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség. | ||
| − | + | A végtelen határérékkel történő számolás szabályai előtt definiálnunk kell néhány kibővített műveletet. Ezt a következők szellemében tesszük: | |
| − | : | + | |
| − | + | ||
| − | + | :Ha ''a'' és ''b'' valamelyike a ∞ szimbólum (a másik, ha nem ilyen, akkor komplex szám), akkor az ''a'' * ''b'' alapműveletet akkor értelmezzük a ''c'' szimbólumként (mely szintén vagy komplex szám, vagy az ∞), ha ''minden'' ''a'' határértékű ''f'' függvény esetén és ''minden'' ''b'' határértékű ''g'' függvény esetén a ''f''*''g'' ''szükségszerűen'' a ''c''-hez tart. Ekkor mondjuk tehát, hogy az | |
| − | : | + | ::''a'' * ''b'' = ''c'' |
| − | :<math>\ | + | :definíció jó. |
| − | + | Például a ∞ + ∞ művelet feltétlenül értelmezett és értéke a ∞, mert könnyen látható, hogy ''bármely'' két, a ∞-hez tartó függvény összege is a ∞-hez tart. De a 0 <math>\cdot</math> ∞ művelet nem értelmezhető, mert van két függvénypár, mely ilyen alakú határértékekkel rendelkezik, de a szorzatuk máshoz tart. Pl.: (1/Re(z)) <math>\cdot</math> Re(z) <math>\to</math> 1, a z=0-ban, de (1/Re(z)) <math>\cdot</math> 2 Re(z) <math>\to</math> 2 a z=0-ban. | |
| − | + | '''Definíció''' – ''Végtelen és alapműveletek'' – Az alábbi műveleti szabályokat vezetjük be a ∞, szimbólumra vonatkozóan, az alábbiakban ''z'' tetszőleges komplex szám, ''n'' tetszőleges nemnulla komplex szám: | |
| − | :<math>\ | + | # <math>\infty+z=\infty </math>, |
| + | # <math>\infty-z=\infty, \quad\quad z-\infty=\infty</math>, | ||
| + | # <math>\infty\cdot\infty=\infty, \quad\quad \infty\cdot n=\infty</math>, | ||
| + | # <math>\frac{z}{\infty}=0 \quad\quad \frac{\infty}{z}=\infty</math>, | ||
| + | továbbá a szorzás és az összeadás kommutatív. | ||
| − | = | + | Megjegyezzük még, hogy <math>\overline{\infty}=\infty</math>, azaz a végtelen konjugáltja saját maga. |
| − | + | '''Definíció''' – ''Határozatlan esetek'' – Az alábbi alapműveletek nem értelmezhetők: | |
| + | # <math>\infty-\infty</math>, | ||
| + | # <math>0\cdot\infty, \quad\quad \infty\cdot 0</math>, | ||
| + | # <math>\frac{\infty}{\infty}</math>, | ||
| + | # <math>\frac{0}{0}</math> | ||
| − | |||
| − | |||
| − | ''' | + | '''Tétel''' – ''Végtelen határérték és alapműveletek'' – Ha az ''f'' és ''g'' komplex függvényeknek létezik határértékük az <math>\scriptstyle{u\in \overline{\mathbf{C}}}</math> helyen, az ''f'' * ''g'' alapművelettl elkészített függvény értelmezési tartományának torlódási pontja ''u'' és a lim<sub>u</sub> ''f'' * lim<sub>u</sub> ''g'' alapművelet elvégezhető, akkor az ''f'' * ''g'' függvénynek is van határértéke ''u''-ban és ez: |
| + | :<math> \lim\limits_u(f\mbox{*}g)=\lim\limits_u f\,\mbox{*}\, \lim\limits_u g \,</math> | ||
| + | Ezenkívül a határozatlan esetekben, amikor a határértékekkel végzett műveletek nem értelmezettek, az alapműveletekkel elkészített függvények határértékeire nem adható általános képlet (mert alkalmasan választott esetekben máshoz és máshoz tartanak). | ||
| − | '' | + | ''A bizonyításról.'' Ennek a tételnek a bizonyítása minden nehézség nélkül elvégezhető vagy az '''R'''<sup>2</sup>-beli sorozatokra vonatkozó átviteli elv vagy a komponensfüggvények határértékére történő hivatkozás útján. Minenekelőtt azt kell szem előtt tartanunk, hogy a végtelenhez való tartás, a függvény abszolútértékének plusz végtelenhez tartását jelenti: |
| − | + | :<math>\exists\lim\limits_{z_0}f=\infty \quad\Longleftrightarrow \quad\exists\lim\limits_{z_0}|f|=+\infty</math> | |
| − | + | ||
| − | + | ||
| − | + | '''Feladat.''' Adjuk példákat arra, hogy a határozatlan alakú határértékeket valóban nem lehet definiálni. | |
| − | '' | + | ''Nézzük a 0-ban az alábbi függvényeket:'' |
| − | :<math>\ | + | :<math>\frac{2}{z}\;-\;\frac{1}{z}=\frac{1}{z}\quad\to \infty</math> miközben <math>(\frac{1}{z}+2)\;-\;\frac{1}{z}=2\quad\to 2</math> |
| − | + | <math>\frac{1}{z}\;\cdot z=1\quad\to 1</math> miközben <math>\frac{2}{z}\;\cdot\;z=2\quad\to 2</math> | |
| − | :<math>\ | + | :<math>\frac{1}{z}/\frac{1}{z}=1\quad\to 1</math> miközben <math>\frac{2}{z}/\frac{1}{z}=2\quad\to 2</math> |
| − | + | ||
| − | + | <math>\frac{z}{z}=1\quad\to 1</math> miközben <math>\frac{2z}{z}=2\quad\to 2</math> | |
| − | + | '''Feladat.''' Számítsuk ki az alábbi határértékeket, ha léteznek! | |
| + | # <math>\lim\limits_{z\to 0}\frac{\mathrm{Im}(z)}{z}</math>, | ||
| + | # <math>\lim\limits_{z\to i}\frac{z-i}{z^2+1}</math>, | ||
| + | # <math>\lim\limits_{z\to 1}\frac{\frac{1}{z-1}+i}{\frac{1}{z^2-1}-i}</math>, | ||
| + | # <math>\lim\limits_{z\to 0}\frac{1}{z}-\frac{2}{\overline{z}}</math>, | ||
| + | # <math>\lim\limits_{z\to -i}\frac{\frac{1}{z+i}+i}{\overline{z}-i}</math>, | ||
| − | == | + | ''Megoldás.'' |
| + | 1. nemnulla ''z''-re: | ||
| + | :<math>\frac{\mathrm{Im}(z)}{z}=\frac{\mathrm{Im}(z)\overline{z}}{z\overline{z}}=\frac{yx-y^2\mathrm{i}}{x^2+y^2}</math> | ||
| + | de ekkor például az első komponensfüggvény ''x'' = 0 felől közelítve 0, míg az ''x'' = ''y''-felől:1/2, azaz nem létezik az első komponensnek a (0,0)-ban határértéke, azaz a komplex függvénynek sem. | ||
| − | + | 2. <math>\frac{z-i}{z^2+1}=\frac{z-i}{(z+i)(z-i)}=\frac{1}{z+i}\quad\longrightarrow_{z\to i}\quad\infty</math> | |
| − | + | ||
| − | + | 3. <math>\frac{\frac{1}{z-1}+i}{\frac{1}{z^2-1}-i}=\frac{ \frac{1+iz-i}{z-1} }{ \frac{1-iz^2+i}{z^2-1} }=\frac{1+iz-i}{z-1}\cdot \frac{(z+1)(z-1)}{1-iz^2+i}</math> | |
| − | + | ::<math>\left.\frac{iz+1-i}{-iz^2+i+1}(z+1)\right|_1=\frac{1}{1}\cdot 1</math> | |
| − | + | ||
| − | = | + | 4. <math>\frac{1}{z}-\frac{2}{\overline{z}}=\frac{\overline{z}-2z}{z\overline{z}}</math> |
| + | csak a valós részt nézve: | ||
| + | :<math>\left|\frac{-x}{x^2+y^2}\right|</math> | ||
| + | az (x,y)=(x,0) esetben a (0,0)-hoz tartva: végtelen, de (x,y)=(0,y), akkor 0. tehát nincs határérték. | ||
| − | + | 5. <math>\lim\limits_{z\to -i}\frac{\frac{1}{z+i}+i}{\overline{z}-i}=\left(\frac{\infty}{0}\right)=\infty</math>. | |
| − | ''' | + | '''Feladat.''' Adjuk meg minden ''z''<sub>0</sub> ∈ '''C''' számra az alábbi függvény határértékét! |
| − | + | # <math>f(z)=\frac{z}{\overline{z}-z}</math>, | |
| + | # <math>f(z)=\frac{z^2}{\overline{z}z-1}</math>, | ||
| + | |||
| + | 1. <math>\mathrm{Dom}(f)=\{z\in \mathbf{C}\mid \overline{z}\ne z\}</math> | ||
| − | + | Folytonos az értelmezési tartományában. A határon: | |
| − | :<math>\ | + | :<math>\frac{z}{\overline{z}-z}=\frac{x+iy}{2iy}\,</math> |
| − | + | ''z''<sub>0</sub> ≠ 0 esetén | |
| − | :<math>\left|\ | + | :<math>\left|\frac{x+iy}{2iy}\right|\geq \frac{|z_0|/2}{2|y|}\to \infty</math> |
| − | + | ''z''<sub>0</sub> = 0 esetén: | |
| − | :<math>\ | + | :<math>\frac{x+iy}{2iy}=\frac{1}{2}-i\frac{x}{2y}</math> |
| − | + | ismert, hogy nincs határérték. | |
| − | + | 2. <math>\mathrm{Dom}(f)=\{z\in \mathbf{C}\mid \overline{z}z\ne 1\}</math> | |
| − | :<math>f(z) | + | |
| − | + | Az egységkör pontjaitól különbözőkre folytonos, az egységkörön a végtelen, a végtelenben pedig nincs határérték. Ugyanis: | |
| − | :<math> | + | :<math>|f(z)|=\frac{|z|^2}{|\overline{z}z-1|}</math>, |
| − | + | így az egységkörön a számláló az 1-hez, a nevező a nullához tart. A végtelenben pedig ''t'' valóssal: | |
| − | :<math>\ | + | :<math>\lim\limits_{t\to +\infty} f(t+0.i)=\lim\limits_{t\to +\infty} \frac{t^2}{t^2-1}= 1\,</math> |
| − | + | :<math>\lim\limits_{t\to +\infty} f(t.i)=\lim\limits_{t\to +\infty} \frac{-t^2}{t^2-1}= -1\,</math> | |
| − | |||
| − | |||
| − | |||
| − | === | + | =='''C'''-differenciálhatóság== |
| + | A komplex differenciálhatóság az előző észrevételekkel szoros kapcsolatban lesz. Egyfelől | ||
| + | :<math>(w\cdot z)'=w\in \mathbf{C}</math> | ||
| + | :<math>(z^2)'=2z\in \mathbf{C}</math> | ||
| + | mutaja, hogy ha a Jacobi-mártix hasonlóképpen viselkedik a komplex számok mátrixreprezentációjában, mint az egyváltozós valós derivált. Másrészt a | ||
| + | :<math>(\overline{z})'=(\begin{smallmatrix} 1 & 0\\0 & -1\end{smallmatrix})\notin \mathbf{C}</math> | ||
| + | mutatja, hogy nem minden valósan deriválható függvény lesz komplex deriválható. Nézzük akkor az egyváltozós valós mintájára a definíciót majd lássuk a komplex differenciálhatóság jellemzését. | ||
| + | |||
| + | '''Definíció''' - ''Komplex differenciálhatóság, komplex derivált'' - Legyen ''f'' a ''z''<sub>0</sub> egy környezetében értelmezett függvény. Azt mondjuk, hogy ''f'' '''C'''-deriválható ''z''<sub>0</sub>-ban és deriváltja a ''w'' szám, ha | ||
| + | :<math>\lim\limits_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}=w</math> | ||
| + | |||
| + | Jelölése: <math>f'(z_0)</math>. | ||
| + | |||
| + | Azt, hogy az f a ''z''<sub>0</sub>-ban komplex deriválható még úgy is jelöljük, hogy | ||
| + | :<math>f\in \mathrm{Diff}_{\mathbf{C}}(z_0)</math>. | ||
| + | |||
| + | Pontbeli deriváltra példa a következő. | ||
| + | |||
| + | '''Példa.''' Milyen ''n'' egész számokra deriválható a 0-ban az alábbi függvény? | ||
| + | :<math>f(z)=\begin{cases}\overline{z}\cdot z^n, & z\ne 0\\ | ||
| + | 0, & z=0 | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | ''Mo.'' Ha ''n''>0, akkor a különbségi hányados: | ||
| + | :<math>\frac{\overline{z}\cdot z^n-0}{z-0}=\frac{\overline{z}\cdot z^n}{z}=\overline{z}\cdot z^{n-1}\to 0</math> ha ''z'' <math>\to</math> 0. | ||
| + | Ha ''n'' = 0, akkor | ||
| + | :<math>\frac{\overline{z}-0}{z-0}=\frac{\overline{z}}{z}=e^{i(-2\varphi)}</math> | ||
| + | aminek nincs határértéke a 0-ban (az egységkörön mozog a végpont). | ||
| + | |||
| + | Ha ''n'' < 0, akkor | ||
| + | :<math>\frac{\overline{z}z^n-0}{z-0}=\frac{\overline{z}}{z^{-n+1}}=\frac{\overline{z}}{z}\frac{1}{z^{-n}}</math> | ||
| + | ami a 0-ban a komplex végtelenbe tart, mert a hossza a végtelenbe tart. | ||
| + | |||
| + | Tehát ''n'' > 0-ra a függvény komplex deriválható a 0-ban, más ''n'' < 1-re nem deriválható. | ||
| + | |||
| + | '''Tétel.''' - ''A komplex differenciálhatóság jellemzése'' - Legyen ''f'' a ''z''<sub>0</sub> = ''x''<sub>0</sub> + i''y''<sub>0</sub> egy környezetében értelmezett függvény. Ekkor az alábbiak ekvivalensek: | ||
| + | :1) <math>f\in \mathrm{Diff}_{\mathbf{C}}(z_0)</math> | ||
| + | :2) <math>f\in \mathrm{Diff}_{\mathbf{R}}(x_0,y_0)</math> és <math>[\mathrm{d}f(x_0,y_0)]\in\mathbf{C}</math>. | ||
| + | |||
| + | ''Bizonyítás.'' Legyen ''f'' a ''z''<sub>0</sub> = ''x''<sub>0</sub> + i''y''<sub>0</sub> egy környezetében értelmezett függvény és ''w'' komplex szám. | ||
| + | Tekintsük a következő határértéket: | ||
| + | :<math>\lim\limits_{z\to z_0}\frac{f(z)-f(z_0)-[w]\cdot (z-z_0)}{|z-z_0|}=0</math> | ||
| + | ahol az ''z'', ''z''<sub>0</sub>, ''f''(''z''), ''f''(''z''<sub>0</sub>) mennyisegekre ugy tekintunk, mint vektorokra. | ||
| + | Ez ekvivalens a következővel: | ||
| + | :<math>\lim\limits_{z\to z_0}\left|\frac{f(z)-f(z_0)}{|z-z_0|}-\frac{w\cdot (z-z_0)}{|z-z_0|}\right|=0</math> | ||
| + | ahol az elobb emlitettek mar algebrai ertelemben komplex szamok, nem feltetlenul vektorok. Azaz | ||
| + | :<math>\lim\limits_{z\to z_0}\left|\frac{z-z_0}{|z-z_0|}\left(\frac{f(z)-f(z_0)}{z-z_0}-w\right)\right|=0</math> | ||
| + | Itt (''z''-''z''<sub>0</sub>)/|''z''-''z''<sub>0</sub>| a komplex egységkörön "futó" függvény, hossza 1, ezért a fenti ekvivalnes a következővel: | ||
| + | :<math>\lim\limits_{z\to z_0}\left|\frac{f(z)-f(z_0)}{z-z_0}-w\right|=0</math> | ||
| + | Ami viszont ugyanakkor igaz mint: | ||
| + | :<math>\lim\limits_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}=w</math> | ||
| + | Ha a következtetésben felfelé vizsgálódunk, tehát feltesszük a komplex deriválhatóságot ahol ''w'' a komplex derivált, akkor azt kapjuk, hogy a ''w'' mátrixreprezentációjával való mátrixszorzás alkalmas lineáris leképezés a valós derivált számára, azaz létezik [df(z<sub>0</sub>)]=[w]. | ||
| + | |||
| + | Másfelől, ha f valósan deriválható és a deriváltja a ''w'' komplex számot reprezentálja, akkor komplexen is deriválható es komplex derivaltja pont ''w''. | ||
| + | |||
| + | '''Cauchy--Riemann-egyenletek''' A fenti tételben a [df(z)] ∈ '''C''' feltétel (természetesen a totális deriválhatóság esetén) ekvivalens az alábbiakkal. Ha ''f'' = ''u'' + i''v'' és ''z'' = ''x'' +i''y'', akkor | ||
| + | :<math>\begin{cases} | ||
| + | \partial_xu=\partial_yv\\ | ||
| + | \partial_yu=-\partial_x v | ||
| + | \end{cases}</math> | ||
| + | |||
| + | '''Komplex deriváltfüggvény''' Ahol egy f komplex függvény komplex deriválható, ott a deriváltja: | ||
| + | :<math>f'(z)=\partial_x u+\mathrm{i}\partial_xv=\partial_y v+\mathrm{i}\partial_xv=\partial_xu-\mathrm{i}\partial_yu=\partial_y v-\mathrm{i}\partial_yu</math> | ||
| + | |||
| + | '''Definíció''' - Regularitás - Az f komplex függvény reguláris a z pontban, ha f a z egy egész környezetén értelmezett, és a teljes környezetben komplex deriválható. | ||
| + | |||
| + | '''Feladat.''' Legyen f(x+iy)=|x|+i|y|. Hol komplex deriválható és hol reguláris f? | ||
| + | |||
| + | '''Feladat.''' Legyen <math>f(x+iy)=x^2+iy^3</math>. Hol komplex deriválható és hol reguláris f? | ||
| + | |||
| + | |||
| + | |||
| + | ===Harmonikus társ keresése=== | ||
| + | |||
| + | Azt mondjuk, hogy a kétszer differenciálható u=u(x,y) valós függvény ''harmonikus'', ha | ||
| + | :<math>u_{xx}''+u_{yy}''\equiv \Delta u\equiv 0\, </math> | ||
| + | itt Δ a Laplace-operátor (nem a Laplace-transzformátor!, hanem a vektoranalízisbeli vektormezőre Hesse-mátrix nyoma). | ||
| + | |||
| + | A C--R-egyenletek mutatják, hogy ha f=u+iv reguláris, akkor u és v harmonikus függvények. Ugyanis: | ||
| + | :<math>u_x'=v_y'\,</math> és | ||
| + | :<math>v_x'=-u_y'\,</math> | ||
| + | De u és v Hesse-mátrixa is szimmetrikus, ezért: | ||
| + | |||
| + | :<math>v_{yy}''=u_{xy}''=u_{yx}''=-v_{xx}''\,</math> | ||
| + | azaz | ||
| + | :<math>\Delta v\equiv 0\,</math> és fordítva. | ||
| + | |||
| + | Általában az a feladat, hogy ha adott u, akkor keressük az ő harmonikus társát, v-t, mellyel u+iv reguláris. Ha tehát adott u, akkor van F és G, hogy | ||
| + | :<math>F=v_y'\,</math> | ||
| + | :<math>G=-v_x'\,</math> | ||
| + | Ami az egzakt differenciálegynlet megoldásánál tanult parciális differenciálegyenlet megoldását igényli v-re, mint potenciálfüggvényre (ekkor f-et komplex pontenciálnak nevezzük, mármint a (<math>v'_x(x,y)</math>,<math>v_y'(x,y)</math>) síkbeli vektormező komplex pontenciáljának; a v valódi pontenciálja lenne. Ennek szükséges utánanézni máshol is!) | ||
| + | |||
| + | '''1..''' Keressünk harmonikus párt az | ||
| + | :<math>u=x^4+y^4-6x^2y^2\,</math> | ||
| + | függvényhez! | ||
| + | |||
| + | ''Mo.'' Van neki, ha Δ=0. Ezt ellenőrizni kell, majd az előző módszerrel megkeresi v-t, amivel u+iv reguláris. | ||
| − | + | <center> | |
| − | + | {| class="wikitable" style="text-align:center" | |
| + | |- bgcolor="#efefef" | ||
| + | |[[Matematika A3a 2008/6. gyakorlat |6. gyakorlat]] | ||
| + | |} | ||
| + | {| class="wikitable" style="text-align:center" | ||
| + | |- bgcolor="#efefef" | ||
| + | |[[Matematika A3a 2008/8. gyakorlat |8. gyakorlat]] | ||
| + | |} | ||
| + | </center> | ||
| − | |||
| − | |||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
A lap jelenlegi, 2016. március 21., 10:39-kori változata
Tartalomjegyzék |
Folytonosság
Azt mondjuk, hogy az A ⊆ C halmazon értelmezett f függvény folytonos a z ∈ A pontban, ha z-ben f folytonos mint R2 ⊇ A  R2 függvény. Maga az f folytonos, ha az értelmezési tartománya minden pontjában folytonos.
R2 függvény. Maga az f folytonos, ha az értelmezési tartománya minden pontjában folytonos.
A többváltozós valós analízisből ismert tény miatt fennáll:
Állítás. Az f komplex függvény pontosan akkor folytonos az értelmezési tartománya egy pontjában, ha ott a függvény valós és képzetes része, mint kétváltozós valós függvény folytonos. Azaz, ha f-et a következő alakban írjuk:
ahol u és v valós értékű függvények (rendre Re(f) és Im(f)), továbbá z0 = x0 + iy0 ∈ Dom(f), akkor a következők ekvivalensek:
- f folytonos a z0-ban
- u és v függvények folytonosak az (x0,y0)-ban
Határérték
Komplex függvény C-beli pontban vett C-beli határértéke ugyanúgy értelmezett, mint az R2 esetben. Itt is érvényes, hogy pontosan akkor látezik a határérték, ha a komponensfüggvényeknek létezik a határértéke és ekkor a határérték egyenlő lesz a valós és képzetes komponens határértékéből alkotott komplex számmal.
A ∞ miatt érdemes külön is megfogalmazni a határérték definícióját, bár az teljesen analóg a valós esettel. Legyen f egy az A ⊆ C halmazon értelmezett, C-be képező függvény. Legyen 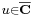 az A torlódási pontja, azaz minden r > 0 esetén legyen olyan a ∈ A, hogy a ∈ Br(u)\{u}. Azt mondjuk, hogy az f-nek a
az A torlódási pontja, azaz minden r > 0 esetén legyen olyan a ∈ A, hogy a ∈ Br(u)\{u}. Azt mondjuk, hogy az f-nek a 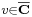 elem határértéke az u-ban, ha
elem határértéke az u-ban, ha
- minden ε > 0 esetén létezik olyan δ > 0, hogy minden z ∈ A ∩ Bδ(u)\{u}-re f(z) ∈ Bε(v)
ahol természetesen a ∞ környezetei a már említett módon értendők.
A kétváltozós függvények közötti határérték-folytonosság kapcsolat is megfogalmazható komplex módon. Itt az f = u + vi függvény határértékén a z = x + iy pontban a limx u + i limy v szám adja. Ekkor
Állítás. Az f komplex függvény pontosan akkor folytonos az értelmezési tartománya egy belső pontjában, ha ott a függvénynek létezik határértéke és az a helyettesítési érték.
A komplex függvények folytonosságának egyik, de nem egyetlen feltétele az, hogy az (u,v) reprezentáció R2-ben lineáris legyen, hiszen a véges dimenziós normált terek között ható lineáris leképezések folytonosak. A nem-folytonosságnál érdemes a határérték nem létezését vizsgálni, hátha ez célra vezet.
Feladat folytonosságra
Feladat. Legyen w ∈ C. Igazoljuk, hogy az alábbi függvények folytonosak!
Megoldás.
Az 1. az R2-ben eltolás a w-nek megfelelő vektorral (Re(w), Im(w))-vel, így affin leképezés, ami folytonos.
2. a w mátrixreprezentációjának megfelelő mátrixszal való szorzás, azaz lineáris leképezés, s így folytonos.
3. azaz a konjugálás: (x,y)  (x,–y) a valós tengelyre való tükrözés, ami szintén lineáris.
(x,–y) a valós tengelyre való tükrözés, ami szintén lineáris.
Végül a reciprok:
így, mint R2 ⊃ R2 függvény:
R2 függvény:
amely olyan, hogy mindkét komponensfüggvénye folytonos valós függvényekből van összeállítva a folytonosságot megőrző módon, azaz az értelmezési tartománya minden pontjában folytonos.
Feladat. Folytonos-e a z = 0-ban az
Megoldás.
Ha z = x + iy és (x,y) ≠ (0,0), akkor:
A komponensfüggvények felírhatók egy 0-hoz tartó és egy korlátos függvény szorzataként:
és
így (x,y) (0,0) esetén a 0-hoz tartanak, így a függvény maga a (0,0)-hoz, azaz a komplex 0-hoz. Mivel itt a függvény értéke 0, ezért f a 0-ban folytonos.
(0,0) esetén a 0-hoz tartanak, így a függvény maga a (0,0)-hoz, azaz a komplex 0-hoz. Mivel itt a függvény értéke 0, ezért f a 0-ban folytonos.
Ha folytonos komplex függvényekből alapműveletek segítségével alkottunk függvényeket, akkor azok is folytonosak maradnak, mert a megfelelő R2-beli függvények ekkor olyanok lesznek, melyek mindegyik komponensfüggvénye a valós alapműveletek segítségével vannak definiálva. Ám, ezek megőrzik a folytonosságot.
Állítás. Ha f és g komplex függvények és az z0 pontban (mindketten értelmezettek és) folytonosak, akkor
- f + g
- f
 g
g
-
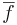
- g(z0) ≠ 0 esetén f/g
is folytonos z0-ban.
Folytonos függvények kompozíciója is folytonos (az kompozíció értelmezési tartományán).
Feladat. Folytonos-e a z = i-ben az
Ha z = x + iy és (x,y) ≠ (0,1), akkor:
Már az első komponens határértéke sem létezik, hisz (x,y)=(0,y) mentén alulról a (0,1)-hez tartva a határérték -1, az x=y-1 mentén pedig -1/gyök kettő.
A második tényező szintén nem.
Feladatok határértékre
Feladat. Igazoljuk definíció szerint, hogy
1. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |z| < δ esetén, hogy a függvényérték a ∞ ε sugarú környezetébe esik, azaz:
Világos, hogy ezt azt jelenti, hogy
amit reciprokvonással kaptunk. Ha tehát ha δ := ε és |z| < δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség.
2. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |z| > 1/δ esetén, hogy a függvényérték a 0-nak ε sugarú környezetébe esik, azaz:
Világos, hogy ezt azt jelenti, hogy
amit reciprokvonással kaptunk. Ha tehát ha δ := ε és |z| > 1/δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség.
A végtelen határérékkel történő számolás szabályai előtt definiálnunk kell néhány kibővített műveletet. Ezt a következők szellemében tesszük:
- Ha a és b valamelyike a ∞ szimbólum (a másik, ha nem ilyen, akkor komplex szám), akkor az a * b alapműveletet akkor értelmezzük a c szimbólumként (mely szintén vagy komplex szám, vagy az ∞), ha minden a határértékű f függvény esetén és minden b határértékű g függvény esetén a f*g szükségszerűen a c-hez tart. Ekkor mondjuk tehát, hogy az
- a * b = c
- definíció jó.
Például a ∞ + ∞ művelet feltétlenül értelmezett és értéke a ∞, mert könnyen látható, hogy bármely két, a ∞-hez tartó függvény összege is a ∞-hez tart. De a 0  ∞ művelet nem értelmezhető, mert van két függvénypár, mely ilyen alakú határértékekkel rendelkezik, de a szorzatuk máshoz tart. Pl.: (1/Re(z))
∞ művelet nem értelmezhető, mert van két függvénypár, mely ilyen alakú határértékekkel rendelkezik, de a szorzatuk máshoz tart. Pl.: (1/Re(z))  Re(z)
Re(z)  1, a z=0-ban, de (1/Re(z))
1, a z=0-ban, de (1/Re(z))  2 Re(z)
2 Re(z)  2 a z=0-ban.
2 a z=0-ban.
Definíció – Végtelen és alapműveletek – Az alábbi műveleti szabályokat vezetjük be a ∞, szimbólumra vonatkozóan, az alábbiakban z tetszőleges komplex szám, n tetszőleges nemnulla komplex szám:
-
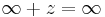 ,
,
-
 ,
,
-
 ,
,
-
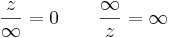 ,
,
továbbá a szorzás és az összeadás kommutatív.
Megjegyezzük még, hogy 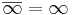 , azaz a végtelen konjugáltja saját maga.
, azaz a végtelen konjugáltja saját maga.
Definíció – Határozatlan esetek – Az alábbi alapműveletek nem értelmezhetők:
-
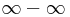 ,
,
-
 ,
,
-
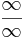 ,
,
-
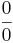
Tétel – Végtelen határérték és alapműveletek – Ha az f és g komplex függvényeknek létezik határértékük az 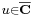 helyen, az f * g alapművelettl elkészített függvény értelmezési tartományának torlódási pontja u és a limu f * limu g alapművelet elvégezhető, akkor az f * g függvénynek is van határértéke u-ban és ez:
helyen, az f * g alapművelettl elkészített függvény értelmezési tartományának torlódási pontja u és a limu f * limu g alapművelet elvégezhető, akkor az f * g függvénynek is van határértéke u-ban és ez:
Ezenkívül a határozatlan esetekben, amikor a határértékekkel végzett műveletek nem értelmezettek, az alapműveletekkel elkészített függvények határértékeire nem adható általános képlet (mert alkalmasan választott esetekben máshoz és máshoz tartanak).
A bizonyításról. Ennek a tételnek a bizonyítása minden nehézség nélkül elvégezhető vagy az R2-beli sorozatokra vonatkozó átviteli elv vagy a komponensfüggvények határértékére történő hivatkozás útján. Minenekelőtt azt kell szem előtt tartanunk, hogy a végtelenhez való tartás, a függvény abszolútértékének plusz végtelenhez tartását jelenti:
Feladat. Adjuk példákat arra, hogy a határozatlan alakú határértékeket valóban nem lehet definiálni.
Nézzük a 0-ban az alábbi függvényeket:
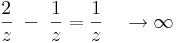 miközben
miközben 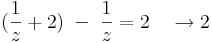
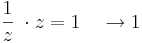 miközben
miközben 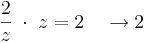
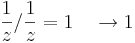 miközben
miközben 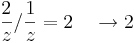
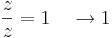 miközben
miközben 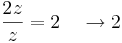
Feladat. Számítsuk ki az alábbi határértékeket, ha léteznek!
-
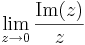 ,
,
-
 ,
,
-
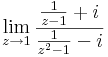 ,
,
-
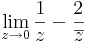 ,
,
-
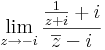 ,
,
Megoldás. 1. nemnulla z-re:
de ekkor például az első komponensfüggvény x = 0 felől közelítve 0, míg az x = y-felől:1/2, azaz nem létezik az első komponensnek a (0,0)-ban határértéke, azaz a komplex függvénynek sem.
2. 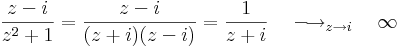
3. 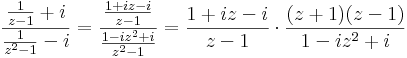
4. 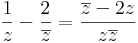 csak a valós részt nézve:
csak a valós részt nézve:
az (x,y)=(x,0) esetben a (0,0)-hoz tartva: végtelen, de (x,y)=(0,y), akkor 0. tehát nincs határérték.
5. 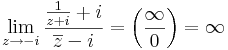 .
.
Feladat. Adjuk meg minden z0 ∈ C számra az alábbi függvény határértékét!
-
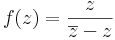 ,
,
-
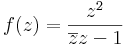 ,
,
1. 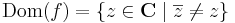
Folytonos az értelmezési tartományában. A határon:
z0 ≠ 0 esetén
z0 = 0 esetén:
ismert, hogy nincs határérték.
2. 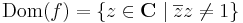
Az egységkör pontjaitól különbözőkre folytonos, az egységkörön a végtelen, a végtelenben pedig nincs határérték. Ugyanis:
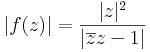 ,
,
így az egységkörön a számláló az 1-hez, a nevező a nullához tart. A végtelenben pedig t valóssal:
C-differenciálhatóság
A komplex differenciálhatóság az előző észrevételekkel szoros kapcsolatban lesz. Egyfelől
mutaja, hogy ha a Jacobi-mártix hasonlóképpen viselkedik a komplex számok mátrixreprezentációjában, mint az egyváltozós valós derivált. Másrészt a
mutatja, hogy nem minden valósan deriválható függvény lesz komplex deriválható. Nézzük akkor az egyváltozós valós mintájára a definíciót majd lássuk a komplex differenciálhatóság jellemzését.
Definíció - Komplex differenciálhatóság, komplex derivált - Legyen f a z0 egy környezetében értelmezett függvény. Azt mondjuk, hogy f C-deriválható z0-ban és deriváltja a w szám, ha
Jelölése: f'(z0).
Azt, hogy az f a z0-ban komplex deriválható még úgy is jelöljük, hogy
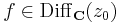 .
.
Pontbeli deriváltra példa a következő.
Példa. Milyen n egész számokra deriválható a 0-ban az alábbi függvény?
Mo. Ha n>0, akkor a különbségi hányados:
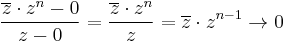 ha z
ha z  0.
0.
Ha n = 0, akkor
aminek nincs határértéke a 0-ban (az egységkörön mozog a végpont).
Ha n < 0, akkor
ami a 0-ban a komplex végtelenbe tart, mert a hossza a végtelenbe tart.
Tehát n > 0-ra a függvény komplex deriválható a 0-ban, más n < 1-re nem deriválható.
Tétel. - A komplex differenciálhatóság jellemzése - Legyen f a z0 = x0 + iy0 egy környezetében értelmezett függvény. Ekkor az alábbiak ekvivalensek:
- 1)
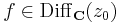
- 2)
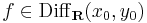 és
és ![[\mathrm{d}f(x_0,y_0)]\in\mathbf{C}](/upload/math/b/9/7/b975f630a8a50e0bde8a08b28b2c681d.png) .
.
Bizonyítás. Legyen f a z0 = x0 + iy0 egy környezetében értelmezett függvény és w komplex szám. Tekintsük a következő határértéket:
ahol az z, z0, f(z), f(z0) mennyisegekre ugy tekintunk, mint vektorokra. Ez ekvivalens a következővel:
ahol az elobb emlitettek mar algebrai ertelemben komplex szamok, nem feltetlenul vektorok. Azaz
Itt (z-z0)/|z-z0| a komplex egységkörön "futó" függvény, hossza 1, ezért a fenti ekvivalnes a következővel:
Ami viszont ugyanakkor igaz mint:
Ha a következtetésben felfelé vizsgálódunk, tehát feltesszük a komplex deriválhatóságot ahol w a komplex derivált, akkor azt kapjuk, hogy a w mátrixreprezentációjával való mátrixszorzás alkalmas lineáris leképezés a valós derivált számára, azaz létezik [df(z0)]=[w].
Másfelől, ha f valósan deriválható és a deriváltja a w komplex számot reprezentálja, akkor komplexen is deriválható es komplex derivaltja pont w.
Cauchy--Riemann-egyenletek A fenti tételben a [df(z)] ∈ C feltétel (természetesen a totális deriválhatóság esetén) ekvivalens az alábbiakkal. Ha f = u + iv és z = x +iy, akkor
Komplex deriváltfüggvény Ahol egy f komplex függvény komplex deriválható, ott a deriváltja:
Definíció - Regularitás - Az f komplex függvény reguláris a z pontban, ha f a z egy egész környezetén értelmezett, és a teljes környezetben komplex deriválható.
Feladat. Legyen f(x+iy)=|x|+i|y|. Hol komplex deriválható és hol reguláris f?
Feladat. Legyen f(x + iy) = x2 + iy3. Hol komplex deriválható és hol reguláris f?
Harmonikus társ keresése
Azt mondjuk, hogy a kétszer differenciálható u=u(x,y) valós függvény harmonikus, ha
itt Δ a Laplace-operátor (nem a Laplace-transzformátor!, hanem a vektoranalízisbeli vektormezőre Hesse-mátrix nyoma).
A C--R-egyenletek mutatják, hogy ha f=u+iv reguláris, akkor u és v harmonikus függvények. Ugyanis:
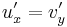 és
és
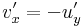
De u és v Hesse-mátrixa is szimmetrikus, ezért:
azaz
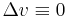 és fordítva.
és fordítva.
Általában az a feladat, hogy ha adott u, akkor keressük az ő harmonikus társát, v-t, mellyel u+iv reguláris. Ha tehát adott u, akkor van F és G, hogy
Ami az egzakt differenciálegynlet megoldásánál tanult parciális differenciálegyenlet megoldását igényli v-re, mint potenciálfüggvényre (ekkor f-et komplex pontenciálnak nevezzük, mármint a (v'x(x,y),vy'(x,y)) síkbeli vektormező komplex pontenciáljának; a v valódi pontenciálja lenne. Ennek szükséges utánanézni máshol is!)
1.. Keressünk harmonikus párt az
függvényhez!
Mo. Van neki, ha Δ=0. Ezt ellenőrizni kell, majd az előző módszerrel megkeresi v-t, amivel u+iv reguláris.
| 6. gyakorlat |
| 8. gyakorlat |
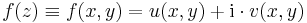
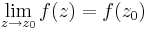
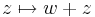
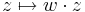
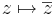
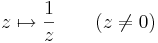
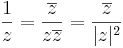
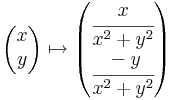
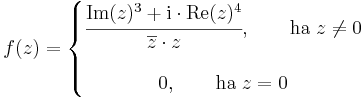
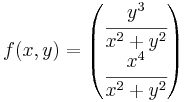
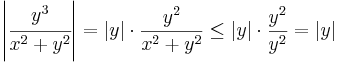
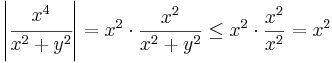
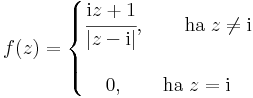
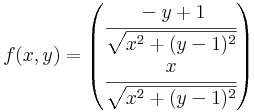
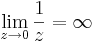
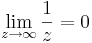
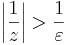
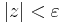
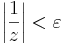
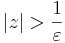
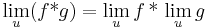
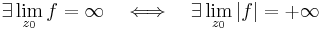
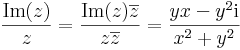
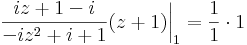
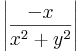
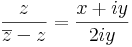
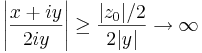
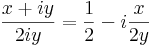
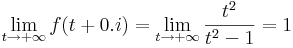
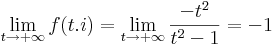

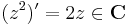
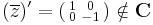
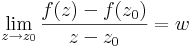
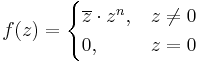
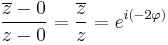
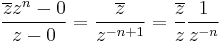
![\lim\limits_{z\to z_0}\frac{f(z)-f(z_0)-[w]\cdot (z-z_0)}{|z-z_0|}=0](/upload/math/c/1/0/c10238bb240c0184bbeacdb2af1ba696.png)