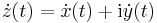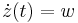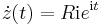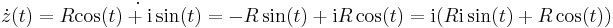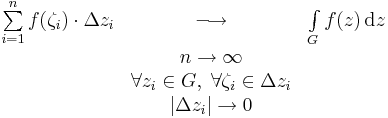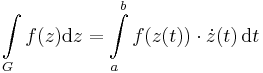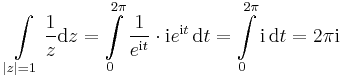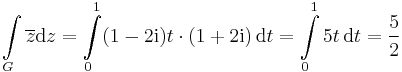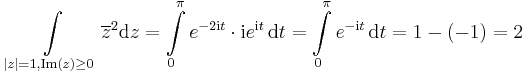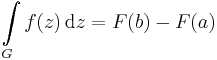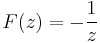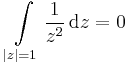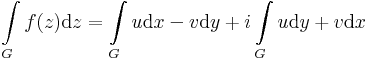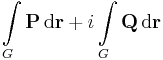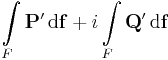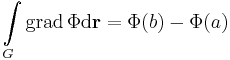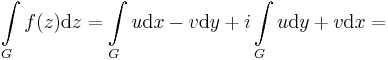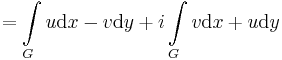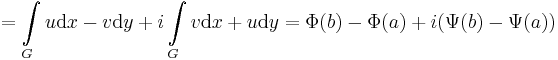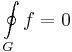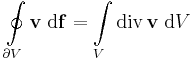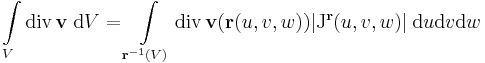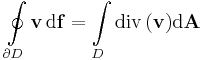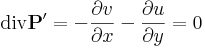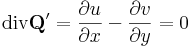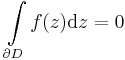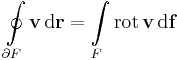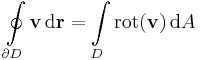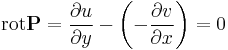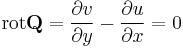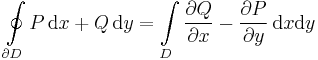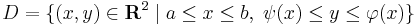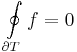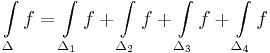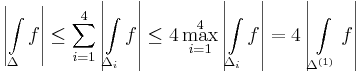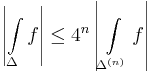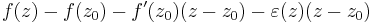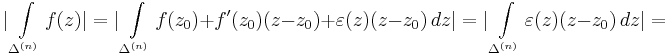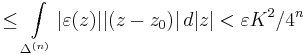Matematika A3a 2008/8. gyakorlat
Tartalomjegyzék |
Komplex integrál
Görbék a komplex síkon
Ha a Γ C-beli halmaz olyan, hogy van olyan G:[a,b] C, t
C, t z(t) folytonos, veges sok kivetellel folytonosan differenciálható fuggveny, aminek az ertekkeszlete Γ, akkor Γ-t görbének nevezzük. A Γ görbe egyszerű, ha nem metszi át saját magát, azaz minden t1, t2-re, ha z(t1) = z(t2), akkor t1 = t2. G zárt, ha z(a) = z(b). A görbe t-beli irányvektorán a
z(t) folytonos, veges sok kivetellel folytonosan differenciálható fuggveny, aminek az ertekkeszlete Γ, akkor Γ-t görbének nevezzük. A Γ görbe egyszerű, ha nem metszi át saját magát, azaz minden t1, t2-re, ha z(t1) = z(t2), akkor t1 = t2. G zárt, ha z(a) = z(b). A görbe t-beli irányvektorán a
komplex számot értjük.
Tobb parameterezes is elo tudja allitani a Γ gorbet. Ezek kozul kettot, a z1-et es a z2-t ekvivalensnek nevezunk, ha van olyan g:[a,b] [c,d] folytonos valos fuggveny, ami (a,b)-n differencialhato, g'>0 es
[c,d] folytonos valos fuggveny, ami (a,b)-n differencialhato, g'>0 es 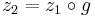 . Az osszes parameterezesek halmaza ket osztalyra esik szet, ezek a gorbe ellentetes parameterezeseit adjak.
. Az osszes parameterezesek halmaza ket osztalyra esik szet, ezek a gorbe ellentetes parameterezeseit adjak.
Példák
1. Legyen t∈[a,b]-re z(t) = x(t) + iy(t) olyan, hogy x(t) = x0 + w1t és y(t) = y0 + w2t, azaz z(t) = z0 + wt. Ekkor z(t) egy egyenes szakasz.
És ekkor:
2. Az origó középpontú R sugarú kör:
- z(t) = Reit t∈[0,2π]
Hiszen ekkor a kör egyenlete:
- x(t) = Rcos(t)
- y(t) = Rsin(t)
ahonnan a komplex írásmódban
- z(t) = x(t) + iy(t) = Rcos(t) + iRsin(t) = R(cos(t) + isin(t))
ami az Euler-formula alapján:
- z(t) = Reit
És ekkor a deriváltja:
hiszen
Ha a kör középpontja z0 = x0 + iy0, akkor
- x(t) = Rcos(t) + x0
- y(t) = Rsin(t) + y0
azaz
- z(t) = Reit + z0
Komplex vonalmenti integrál
Definíció. Ha G:[a,b] C görbe és f olyan komplex függvény, melyre Ran(G)⊆Dom(f), és f folytonos, akkor belátható, hogy létezik a
C görbe és f olyan komplex függvény, melyre Ran(G)⊆Dom(f), és f folytonos, akkor belátható, hogy létezik a
határérték, mely egy speciális Riemann-közelítőösszeg határértéke. Itt a görbén kijelöltük a véges sok zi pontot, melyek a szigorúan monoton (ti)-khez tartoznak a zi = z(ti) definícióval. Ezen [z(ti),z(ti + 1)] görbeszakaszokon belül felvettük tetszőlegesen a ζi közbülső pontokat, és a Δzi=[z(ti),z(ti + 1)] szakaszokkal elkészítettük az f(ζi)Δzi komplex szorzatokat. A határérték ezek görbére vett összegének határértéke. Ez a határérték az f függvény G-re vett komplex integrálja.
Kiszámítási formula. Belátható, hogy a fenti integrál a következőkkel egyenlő:
Megjegyzes A helyettesiteses integralas tetelenek felhasznalasaval belathato, hogy ez az integral fuggetlen a parametertezestol, ha azok ugyanazt az iranyitast hatarozzak meg.
Megj. A kiszamitasi formulaban skalarvaltozos vektorerteku fuggveny integralja szerepel. Ezt a kovetkezokeppen kell kiszamitani:
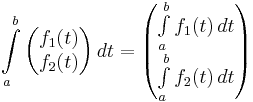
Példa
1. a) Legyen G a komplex egységkör pozitívan irányítva.
Ahol a valós Newton--Leibniz-formulát alkalmaztuk a komponensfüggvényekre.
- b) Integráljuk az
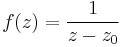
függvény a z0 középpontú R sugarú pozitívan irányított körre, azaz a | z − z0 | = R egyenletű görbére.
Ekkor a görbe paraméterezése:
- z(t) = Reit + z0,
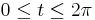
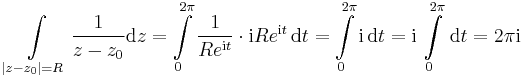
2. Legyen G a z(t)=(1+2i)t, ahol t∈[0,1].
3. Legyen G a komplex egységkör felső fele, pozitívan irányítva.
Komplex Newton--Leibniz-formula
Ha az f komplex függvény, olyan, hogy van olyan komplex differenciálható F, melyre F'=f, akkor azt mondjuk, hogy az F az f primitív függvénye.
Komplex Newton--Leibniz-formula. Ha a nyílt halmazon értelmezett f komplex függvénynek primitív függvénye az F, akkor minden az f értelmezési tartományában haladó G:[a,b] C görbére:
C görbére:
(Ha még nem tudjuk, hogy reguláris függvény analitikus, akkor f-ről fel kell tennünk, hogy folytonos.)
4. Legyen 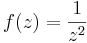 . Mi az egységkörre az integrálja?
. Mi az egységkörre az integrálja?
primitívfüggvénye f-nek, ezért
hiszen zárt a görbe, azaz a pr. fv. a kezdő és végpontban ugyanannyi.
Visszavezetés valós vonalintegrálra es feluleti integralra
Az integrál kifejezhető vonalintegrállal. Ha ugyanis f= u + iv, akkor az f=(u,v) vektormezőnek olyan differenciálforma szerinti integrálja a komplex pályamenti integrál, mely az f=(u,v) vektor és a dz=(dx,dy) infinitezimális elmozdulásvektor komplex szorzásaként jön létre:
Ebben a felírásban az (u,-v) és (v,u) olyan segédvektormezők, melyek vonalintegráljai adják meg a komplex integrál valós és képzetes részét. Tehát az integrált a
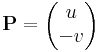 és
és 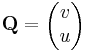
segédvektormezők síkbeli vonalintegráljai
vagy
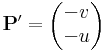 és
és 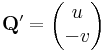
segédvektormezők síkbeli felületi integráljai
szolgáltatják.
Itt érdemes feleleveníteni, hogy az v = (v1, v2) síkvektormező felületi integráljat a (v1, v2)(df1, df2) "differencialforma" integralasa adja. Itt az infinitezimalis feluletelem (df1, df2)=(dy,-dx).
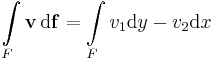 .
.
A N.--L.-tétel bizonyitasa. A vonalintegrálra vonatkozó Newton--Leibniz-tétel (I. gradiens tétel) a következő: ha Φ folytonosan differenciálható, az értelmezési tartományában haladó G görge végpontjai: a és b, akkor
Ezt a segédvektormezőkre fogjuk alkalmazni.
- F = Φ + iΨ
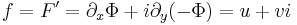
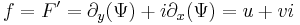

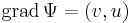
u,v folytonos differenciálhatósága sajnos csak egy későbbi tétel következménye, miszerint reguláris függvény analitikus. Addig a tételben ideiglenesen ki kell kötnünk, hogy f folytonos.
Tétel. Ha a D nyílt halmazon értelmezett f függvénynek van primitív függvénye, akkor f körintegrálja minden a D-ben haladó zárt görbére nulla:
További információhoz akkor jutunk, ha a többváltozós analízis cirkulációmentességi feltételeit vizsgáljuk. Ehhez a vissza kell vezetni a komplex integrált a vonalintegrálra.
Cirkulációmentesség
Gauss-tétel
Lássuk először Gauss-tétellel, hogyan következtethetünk a körintegrál eltűnésére.
Gauss-tétel (R3-ra) Legyen v nyílt halmazon értelmezett C1-függvény, V merheto, peremes térrész és legyen ennek pereme a ∂V kifelé irányított felület. Ha V a peremével együtt Dom(v)-ben van, akkor
Megjegyzes. Az itt szereplő fogalmak közül néhányról beszélnünk kell.
Felület. Legyenek a φi:Di  R3 függvények folytonosan differenciálhatóak és injektívek int(Di)-n, melyek mérhető tartományok R2-ben. Ha a képeik egymásba nem nyúlók, azaz int(φi(Di)) ∩ int(φj(Dj)) üres, ha i ≠ j, és a képek uniója összefüggő halmaz, akkor U Ran(φi)-t előállítottuk paraméteres felületként.
R3 függvények folytonosan differenciálhatóak és injektívek int(Di)-n, melyek mérhető tartományok R2-ben. Ha a képeik egymásba nem nyúlók, azaz int(φi(Di)) ∩ int(φj(Dj)) üres, ha i ≠ j, és a képek uniója összefüggő halmaz, akkor U Ran(φi)-t előállítottuk paraméteres felületként.
Példaként említhetjük a kúp paraméterezését:
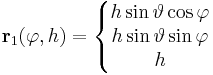 , ha φ ∈ [0,2π] és h ∈ [0,H]
, ha φ ∈ [0,2π] és h ∈ [0,H]
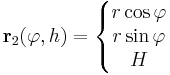 , ha φ ∈ [0,2π] és r ∈ [0,R]
, ha φ ∈ [0,2π] és r ∈ [0,R]
ahol H a kúp magassága, R az alapkörsugara, θ a félkúpszöge (z a tengelye, O a csúcsa). Tehát itt a paramétertartományok [0,2π] × [0,H] és [0,2π] × [0,R].
C1-ség. Ez azért kell, mert a térfogati integrált a D paramétertartományon a
képlettel számoljuk és ahhoz, hogy ez létezzen, ahhoz pl. az kell, hogy ne csak az r = r(u,v,w) legyen folytonosan diff.-ható, de a divergencia is folytonos legyen.
Gauss-tétel (R2-re) Legyen D mérhető peremes síkrész, melynek perme, azaz a ∂D halmaz kifelé irányított síkbeli felület. Ha v nyílt halmazon értelmezett folytonosan R-differenciálható és Dom(v) tartalmazza D lezártját, akkor
ahol ∫df kétdimenziós felületi integrált jelöl, ∫dA pedig kétdimenziós tartományi integrált.
Így tehát a komplex vonalintegrál kiszámításához csak a P' és Q' felületi integrálját kell kiszámítanunk, amihez a Gauss-tételbeli divergenciákat kell kiszámítanunk:
Ami, a C-R-egyenletek miatt igaz.
Innen
Stokes-tétel
Nézzük meg Stokes-tétellel is a bizonyítást.
Stokes-tétel (R3-ra) Legyen a nyílt halmazon értelmezett v vektorfüggvény folytonosan differenciálható, a Dom(v)-beli F felületen, aminek a ∂F pereme legyen szintén Dom(v)-beli és F-hez megfelelően irányított görbe. Ekkor
Megjegyzes. A térbeli cirkulációmentességre vonatkozó nevezetes tétel ezzel a tétellel kapcsolatos. Ebben az esetben, bár az egyszeres összefüggőség nincs megkötve Dom(v)-re vonatkozólag, előjön a következményében:
Következmény. Ha az egyszeresen összefűggő U nyílt halmazon értelmezett v vektormező folytonosan differenciálható, akkor az alábbi három kijelentés ekvivalens egymással:
- rot v eltűnik U-n,
- minden U-ban haladó zárt görbén a v körintegrálja nulla,
- létezik v-nek U-n potenciálja, azaz olyan Φ : U
 R függvény, melyre grad Φ = v.
R függvény, melyre grad Φ = v.
Itt az egyszeres összefüggőség azért kell, mert ilyen esetben a zárt görbéhez található olyan felület, mely a tartományban halad és pereme a görbe.
Stokes-tétel (R2-re) Legyen a D síkbeli tartomany határa a ∂D zárt görbe, megfelelően irányítva. Ha v folytonosan R-differenciálható egy nyílt halmazon, mely tartalmazza D lezártját, akkor
Ekkor csak a rotációt kell kiszámítanunk:
Ami, a C-R-egyenletek miatt igaz.
Mindezekből tehát következik, hogy ha a D peremes síktartomány lezártján az f komplex függvény (értelmezett és) analitikus, akkor D peremén az f integrálja eltünik. A következőkben élesítjük úgy a tételt, hogy elegendő legyen feltenni benne, hogy f egyszer komplexen deriválható, egyszeresen összefüggő nyílt halmazon értelmezett és a görbe egy benne haladó egyszerű zárt görbe.
Green-tétel
A síkbeli Stokes-tételt néha Green-tételnek is nevezik, ha az alábbi alakban van írva. Ez a következő. Legyen a D síkbeli tartomany határa a ∂D zárt görbe, megfelelően irányítva. Ha a (P,Q) síkbeli vektormező folytonosan R-differenciálható egy nyílt halmazon, mely tartalmazza D lezártját, akkor
HF: Bizonyítsuk be a tételt síkbeli normáltartományra, azaz olyan D-re, melyre:
ahol minden x∈[a,b]-re ψ(x)≤φ(x). Itt ψ, φ folytonosan differenciálható.
Goursat-lemma, Cauchy-féle integráltétel
Goursat ennél is mélyebb eredményt talált:
Goursat-lemma. A T háromszöglapon reguláris f komplex függvény integrálja a háromszög határán nulla:
Bizonyitas. A haromszoget osszuk fel 4 egybevago haromszogre: Δ=Δ1∪Δ2∪Δ3∪Δ4. Ha jol iranyitjuk a kis haromszogek hatarat, akkor
Ezt felulbecsulhetjuk a kovetkezovel:
most Δ(1)-et bontjuk fel es folytatva a felosztast egy nullahoz tarto nagysagu haromszogekbol allo egymasba skatulyazott (Δ(n)) haromszogsorozatot kapunk, mely egy ponthoz, a z0-hoz tart. A haromszogek kerulete K/2n, ha K az eredeti haromszog kerulete. Erra a sorozatra tovabba:
igaz.
Most felhasznaljuk a komplex differencialhatosagot. Tetszoleges ε>0 szamra van olyan kornyezete z0-nak, es a haromszogsorozatnak olyan N indexe, melyre az n-edik tagok mar a kornyezetben vannak es az alabbi formulaban az |ε(z)|<ε:
Ezt integralva a haromszogre:
Itt az utolso kifejezest az ivhossz integrallal felulbecsuljuk:
Mivel ε tetszoleges volt, ezert az integral eltunik.
Innen már könnyen adódik a komplex analízis főtétele, melyet először Cauchy modott ki ugyan csak folytonosan diffható komplex függvényre, de Goursat ezt megfejelte a gyengített feltételével:
Főtétel. Ha a D egyszeresen összefüggő tartományon reguláris az f komplex függvény, akkor a tartományban minden zárt G egyszeru görbén a függvény integrálja nulla:
Nehany topologiai fogalom
Egy D nyilt halmaz C-ben egyszeresen osszefuggo, ha benne minden zart gorbe pontra deformalhato.
Ez utobbi a kovetkezot jelenti. Azt mondjuk, hogy a γ:[a,b] D zart gorbe a z0 D-beli pontra deformalhato a D tartomanyban, ha letezik olyan Γ:[0,1]
D zart gorbe a z0 D-beli pontra deformalhato a D tartomanyban, ha letezik olyan Γ:[0,1] D[a,b] gorbe erteku fuggveny, melyre Γ(1)=γ, Γ(0)=z0 konstans gorbe es Γ az [a,b] es D[a,b] terek kozott hato folytonos lekepezes a szupremumnorma szerint.
D[a,b] gorbe erteku fuggveny, melyre Γ(1)=γ, Γ(0)=z0 konstans gorbe es Γ az [a,b] es D[a,b] terek kozott hato folytonos lekepezes a szupremumnorma szerint.
Csillagszeru egy H halmaz C-ben, ha van olyan H-beli pont c pont, hogy barmely H-beli z pontra a [cz] szakasz H-ban van.
Pelda. Egy csillagszeru tartomany egyszeresen osszefuggo, mert a csillagpontra valo [0,1]-beli aranyszammal parameterezett kozeppontos kicsinyites kepei alkotta parameteres gorbesereg ilyen.