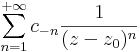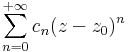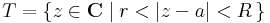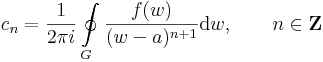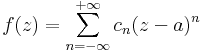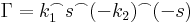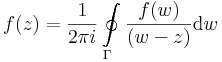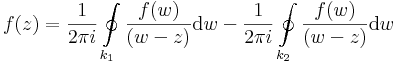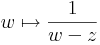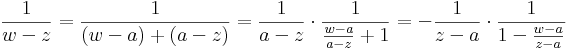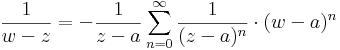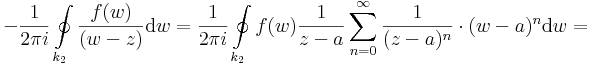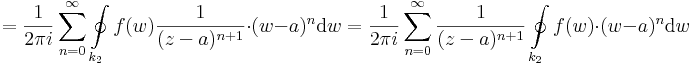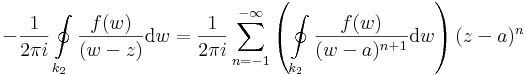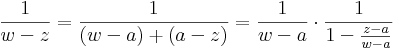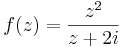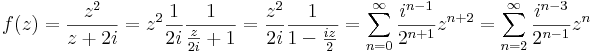Matematika A3a 2008/8. gyakorlat
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Taylor-sor) |
||
| 28. sor: | 28. sor: | ||
'''3. ''' Mint minden hatványsor ez is egyenletesen konvergál az összegfüggvényéhez, így tagonként deriválható és integrálható. | '''3. ''' Mint minden hatványsor ez is egyenletesen konvergál az összegfüggvényéhez, így tagonként deriválható és integrálható. | ||
| + | |||
| + | |||
| + | ==Egész kitevőjű hatványsorok, Laurent-sor== | ||
| + | |||
| + | '''Definíció.''' Ha adott ''a'' számra és (''c''<sub>n</sub>)<sub>n∈'''Z'''</sub> komplex számok komplex számokra a | ||
| + | :<math>\sum\limits_{(-\infty)}(c_n(id-a)^n)</math> | ||
| + | függvénysort egész kitevőjű hatványsornak, vagy Laurent-sornak nevezzük. Egy ilyen sor összegfüggvénye: | ||
| + | :<math>\sum\limits_{n=-\infty}^{+\infty}c_n(z-a)^n</math> | ||
| + | |||
| + | Ugyanúgy, ahogy minden nemnegatív kitevőjű hatványsor egyenlő a saját Taylor-sorával, így az ilyen sorokat egyszerűen csak Laurent-sornak hívjuk, függetelenül attól, hogy a Laurent-sor együtthatóit egy függvény értékeiből számoljuk ki. | ||
| + | |||
| + | Ahogy a Taylor-sorfejtésben nagyon hasznos a mértani sor összegképlete (és konvergenciafeltétele), úgy ez a Laurent-soroknál is jól alkalmazható: | ||
| + | |||
| + | '''Példa.''' Mely pontok körül fejthető egész kötevőjű hatványsorba a | ||
| + | :<math>f(z)=\frac{1}{z} \,</math> | ||
| + | függvény és mik a konvergenciatartományok? | ||
| + | ''Megoldás.'' | ||
| + | |||
| + | 1) z ≠ 0-ra reguláris, így minden <math>z_0</math> ≠ 0-ra Taylor-sorba fejthető legalább is a <math>z_0</math> egy olyan környzetében, mely a 0-t mint szingularitást nem tartalmazza (hisz tudjuk: hatványsor konvergenciatartománya körlap). Ez a sor: | ||
| + | |||
| + | :<math>\frac{1}{z-z_0+z_0}=\frac{1}{z_0}\cdot\frac{1}{z-z_0+1}=\frac{1}{z_0}\cdot\frac{1}{1-(-1)(z-z_0)}=</math> | ||
| + | ::<math> =\frac{1}{z_0}\cdot\sum\limits_{n=0}^{\infty}(-1)^n(z-z_0)^n=\sum\limits_{n=0}^{\infty}\frac{(-1)^n}{z_0}(z-z_0)^n</math> | ||
| + | A sugara 1, hisz |(-1)||z-<math>z_0</math>|<1 kell, ami ugyanaz, mint |z-<math>z_0</math>|<1. Persze, ha |<math>z_0</math>| < 1, akkor a sugár, maga a |<math>z_0</math>|, hisz a 0-t nem állítja elő a sor. | ||
| + | |||
| + | 2) <math>z_0</math> ≠ 0-ra a Laurent-sora. Most a <math>z-z_0</math>-nak a mértani sorrá alakítás után a nevezőbe kell kerülnie: | ||
| + | :<math>\frac{1}{z-z_0+z_0}=\frac{1}{z-z_0}\cdot\frac{1}{1+\frac{z_0}{z-z_0}}=\frac{1}{z-z_0}\cdot\frac{1}{1-\frac{-z_0}{z-z_0}}=</math> | ||
| + | ::<math> =\frac{1}{z_0}\cdot\sum\limits_{n=0}^{\infty}\frac{(-1)^nz_0^n}{(z-z_0)^n}=\sum\limits_{n=0}^{-\infty}(-1)^{-n}z_0^{-n}(z-z_0)^n</math> | ||
| + | Ennek a sorfejtésnek akkor van jelentőssége, amikor olyan pont körüli sorral akarunk egy ''z'' számot előállítani, melynek minden ''z''-t tartalmazó gömbi környzete tartalmazza a 0-t is. | ||
| + | |||
| + | Konvergenciaköre a | ||
| + | :<math>|z-z_0|>|z_0|\;</math> | ||
| + | egyenlőtlenségnek eleget tévő ''z''-k. | ||
| + | |||
| + | 3) z = 0-ban is van Laurent-sora, éspedig önmaga: | ||
| + | :<math>f(z)=...+0+\frac{1}{z}+0+... \,</math> | ||
| + | Ennek a sugarai R<sub>-</sub>=0, mert a (...0,0,1) sorozat n-edik gyökeinek limszupja 0, és R<sub>-</sub>=+∞, mert a (0,0,0,0,0,...) sorozat n-edik gyökeinek limszupja 0 és "reciproka" + végtelen. (Ez egyben a ∞ körüli Laurent-sor, melynek csak reguláris része van.) | ||
| + | |||
| + | ===Konvergenciatartomány=== | ||
| + | Laurent-sornál a konvergenciatartomány egy körgyűrű, melynek sugarait az együtthatókból a Cauchy--Hadamard-tételhez hasonló módon számolható, éspedig: | ||
| + | |||
| + | :<math>R_+=\frac{1}{\limsup\limits_{n>0}\sqrt[n]{|c_n|}}\,</math> | ||
| + | :<math>R_-=\limsup\limits_{n<0}\sqrt[n]{|c_n|}\,</math> | ||
| + | |||
| + | Ez a kijelentés könnyen igazolható a Cauchy-féle gyökkritériummal, sőt a Cauchy--Hadamard-tétel bizonyítását felidézve szinte magától értetődik. | ||
| + | |||
| + | ===Reguláris- és főrész === | ||
| + | A Laurent-sor | ||
| + | :<math>\sum\limits_{n=1}^{+\infty}c_{-n}\frac{1}{(z-z_0)^n}\,</math> | ||
| + | részét a sor '''főrészének,''' a | ||
| + | :<math>\sum\limits_{n=0}^{+\infty}c_{n}(z-z_0)^n\,</math> | ||
| + | részét a sor '''reguláris''' részének nevezzük. | ||
| + | |||
| + | ==Laurent-sorfejtés== | ||
| + | |||
| + | '''Tétel.''' -- A Laurent-sor tétele -- Ha az ''f'': '''C''' <math>\supset\!\to</math> '''C''' és ''a'' ∈ '''C''' szám és 0 ≤ r < R ≤ +∞ olyan sugarak, hogy ''f'' az | ||
| + | :<math>T=\{z\in \mathbf{C}\mid r<|z-a|<R\,\}</math> | ||
| + | nyílt körgyűrűben reguláris, akkor egyértelműen léteznek olyan (''c''<sub>n</sub>)<sub>n∈'''Z'''</sub> komplex számok, éspedig tetszőleges a ''T''-ben haladó az a-t egyszer pozitív irányban körbehurkoló ''G'' görbére: | ||
| + | :<math>c_n=\frac{1}{2\pi i}\oint\limits_{G}\frac{f(w)}{(w-a)^{n+1}}\mathrm{d}w,\quad\quad n\in\mathbf{Z}</math> | ||
| + | hogy a | ||
| + | :<math>\sum\limits_{(-\infty)}(c_n(id-a)^n)</math> | ||
| + | függvénysor konvergens ''T''-ben és minden ''z'' ∈ ''T'' számra: | ||
| + | :<math>f(z)=\sum\limits_{n=-\infty}^{+\infty}c_n(z-a)^n</math> | ||
| + | |||
| + | ''Bizonyítás.'' ''f''-et most nem tudjuk előállítani a Cauchy-integrálformulával, mint a Taylor-sor esetén, mert az ''a'' pontban esetleg a függvény nem reguláris. De előállíthatjuk két hasonló formula különbségeként. | ||
| + | |||
| + | Rögzítsük egy tetszőlegesen választott ''z'' ∈ ''T''-t. Legyenek ''k''<sub>1</sub> és ''k''<sub>2</sub> két ''a'' középpontú, ''T''-ben haladó, pozitívan irányított kör, úgy, hogy ''z'' a ''k''<sub>1</sub> és ''k''<sub>2</sub> körök közötti nyílt tartományba essen. Ezekből a körökből és az őket elválasztó gyűrűt sugárirányban befelé átmetsző s szakaszból elkészítünk egy olyan zárt görbét, melyre már alkalmazható az integrálformula. Tekintsük úgy, hogy ''k''<sub>1</sub> kezdő és végpontja az ''s'' kezdőpontja, ''k''<sub>2</sub> kezdő és végpontja pedig az ''s'' végpontja. Legyen | ||
| + | :<math>\Gamma=k_1^\frown s^\frown (-k_2)^\frown(-s)</math> | ||
| + | itt (-s) az ''s''-sel ellenkező irányítású szakaszt jelzi. Ekkor Γ a ''z''-t egy reguláris tartományban hurkolja egyszer, pozitívan körbe, így a Cauchy-integrálformulával: | ||
| + | :<math>f(z)=\frac{1}{2\pi i}\oint\limits_{\Gamma}\frac{f(w)}{(w-z)}\mathrm{d}w</math> | ||
| + | Node, ebben az integálban az s íven kétszer oda-vissza végezzük el az integrálást, így az erre vett integrál eltűnik. Másrészt a (-''k''<sub>2</sub>)-n vett integrál ellenkezője a 'k''<sub>2</sub>-vettének, így végülis: | ||
| + | :<math>f(z)=\frac{1}{2\pi i}\oint\limits_{k_1}\frac{f(w)}{(w-z)}\mathrm{d}w-\frac{1}{2\pi i}\oint\limits_{k_2}\frac{f(w)}{(w-z)}\mathrm{d}w</math> | ||
| + | Hangsúlyozzuk, hogy ''z'' és ''a'' most konstansok, így a | ||
| + | :<math>w\mapsto\frac{1}{w-z}\,</math> | ||
| + | az értelmezési tartományán analitikus függvény. Ennek -- szikásos módon a mértani sor összegére vonatkozó képlet segítségével -- elvégezhetjük az ''a'' középpontú, valamilyen körön belüli hatványsorba fejtését. Természetesen a |w-a| < |z-a| feltételt meg kell követelnünk, hiszen hatványsor konvergenciakörében nem lehet benne a ''z'' szakadási pont. Tegyük fel tehát, hogy |w-a| < |z-a|. Ekkor: | ||
| + | :<math>\frac{1}{w-z}=\frac{1}{(w-a)+(a-z)}=\frac{1}{a-z}\cdot\frac{1}{\frac{w-a}{a-z}+1}=-\frac{1}{z-a}\cdot\frac{1}{1-\frac{w-a}{z-a}}</math> | ||
| + | Ezzel megvan a sorfejtés minden együtthatója, ugyanis <math>q=\frac{w-a}{z-a}</math>-ra kell alkalmazni a mértani sor formuláját: | ||
| + | :<math>\frac{1}{w-z}=-\frac{1}{z-a}\sum\limits_{n=0}^{\infty}\frac{1}{(z-a)^n}\cdot(w-a)^n</math> | ||
| + | 1) Világos, hogy ezt a sorfejtést csak a ''k''<sub>2</sub>-re vonatkozó integrálban használhatjuk fel, mert ott lesz a q < 1 (ill. a w mindig közelebb a-hoz mint z-hez). Ezt az integrált tehát: | ||
| + | :<math>-\frac{1}{2\pi i}\oint\limits_{k_2}\frac{f(w)}{(w-z)}\mathrm{d}w=\frac{1}{2\pi i}\oint\limits_{k_2}f(w)\frac{1}{z-a}\sum\limits_{n=0}^{\infty}\frac{1}{(z-a)^n}\cdot(w-a)^n\mathrm{d}w=</math> | ||
| + | az integrál felcserélhető a szummával és a w-től független tagok kihozhatók az integrál elé, ezért | ||
| + | :<math>=\frac{1}{2\pi i}\sum\limits_{n=0}^{\infty}\oint\limits_{k_2}f(w)\frac{1}{(z-a)^{n+1}}\cdot(w-a)^n\mathrm{d}w=\frac{1}{2\pi i}\sum\limits_{n=0}^{\infty}\frac{1}{(z-a)^{n+1}}\oint\limits_{k_2}f(w)\cdot(w-a)^n\mathrm{d}w</math> | ||
| + | Ekkor egy konvergens, negatív kitevőjű hatványsort kaptunk, melynek csak főrésze van, de érdekes módon nem a középponttal és w-re, hanem a középponttal és z-ra. Ez pont a kívánt sorfejtés, melyet érdemes átindexelni úgy, hogy a szummázás -1-től induljon és -∞-ig menjen: | ||
| + | :<math>-\frac{1}{2\pi i}\oint\limits_{k_2}\frac{f(w)}{(w-z)}\mathrm{d}w=\frac{1}{2\pi i}\sum\limits_{n=-1}^{-\infty}\left(\oint\limits_{k_2}\frac{f(w)}{(w-a)^{n+1}}\mathrm{d}w\right)(z-a)^{n}</math> | ||
| + | |||
| + | Már csak azt kell megmagyaráznunk, hogy a ''k''<sub>2</sub> helyére most már minden olyan G görbére felírható, mely az ''a''-t pozitívan öleli körbe egyszer és a regularitási tartományban halad. Valóban, a képletbeli integrál már független az 1/(w-z) sorfejtési szituációjától és minden olyan G görbére áttranszformálható melyek folytonosan áttranszformálható ''k''<sub>2</sub>-be. Ez a ''T'' körgyűrű összes a tételi állításban megadott görbéjére áll. | ||
| + | |||
| + | 2) Most már az előző számolásból sejthető, hogy a Laurent-sor reguláris része akkor jön ki, ha az 1/(w-z) reciprokfüggvényt a az ''a'' körül nem pozitív, hanem negatív kitevőjű hatványsorba, fejtjük -- mint az első példában. Ezt a |w-a| > |z-a| feltétellel tehetjük csak meg, hisz ilyen sor konvergenciatartománya körgyűrű és a z szinguláris pontot nem tartalmazhatja: | ||
| + | |||
| + | :<math>\frac{1}{w-z}=\frac{1}{(w-a)+(a-z)}=\frac{1}{w-a}\cdot\frac{1}{1-\frac{z-a}{w-a}}</math> | ||
| + | Ez a sor valóban akkor konvergens, ha |w-a| > |z-a|. Ezzel az előző pomt számolását elvégezve az f(z)-t előállító Laurent-sor reguláris részét kapjuk. QED | ||
| + | |||
| + | |||
| + | '''Példa.''' Adjuk meg az | ||
| + | :<math>f(z)=\frac{z^2}{z+2i}\,</math> | ||
| + | függvény azon 0 körüli Laurent-sorát, mely előállítja az 1-et! Azt is adjuk meg, mely a -3-t állítja elő! | ||
| + | |||
| + | ''Megoldás.'' -2i szinguláris hely. Ha a=0, akkor a z=1-et a 0 körüli Taylor-sor állítja elő, mert |0-1| < |0 - (-2i)|. Persze ezt is a m.s-ral adjuk meg: | ||
| + | :<math>f(z)=\frac{z^2}{z+2i}=z^2\frac{1}{2i}\frac{1}{\frac{z}{2i}+1}=\frac{z^2}{2i}\frac{1}{1-\frac{iz}{2}}=\sum\limits_{n=0}^{\infty}\frac{i^{n-1}}{2^{n+1}}z^{n+2}=\sum\limits_{n=2}^{\infty}\frac{i^{n-3}}{2^{n-1}}z^n</math> | ||
A lap 2013. október 23., 07:52-kori változata
Tartalomjegyzék |
Taylor-sor
A Cauchy-féle integrálformula következménye a következő tétel, mely a komplex differenciálelmélet egyik megjellegzetesebb eredménye:
Tétel. Ha az f: C 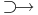 C függvény az értelmezési tartománya egy z0 pontjában és ennek egy nyílt környezetében komplex differenciálható (azaz z0-ban reguláris), akkor f a z0 pont egy V = Bδ(z0) környezetén mindenhol végtelenszer differenciálható, V minden pontjában az f z0-beli Taylor-sora konvergens és ennek határfüggvénye V-n előállítja f-et:
C függvény az értelmezési tartománya egy z0 pontjában és ennek egy nyílt környezetében komplex differenciálható (azaz z0-ban reguláris), akkor f a z0 pont egy V = Bδ(z0) környezetén mindenhol végtelenszer differenciálható, V minden pontjában az f z0-beli Taylor-sora konvergens és ennek határfüggvénye V-n előállítja f-et:
(azaz f analitikus z0-ban).
A tétel tehét azt mondja ki, hogy "reguláris függvény analitikus".
Megjegyezzük, hogy 1. mint minden nemnegatív egész hatványokat tartalmazó hatványsor, a Taylor-sor is egy körlap belsején abszolút konvergens, mely körlap sugara a konvergenciasugára, mely
ahol a sor a ∑an(z-z0)n, a körlap középpontja z0, és ahol a reciprok kivételesen úgy értendő, hogy 1/0 = ∞, 1/∞ = 0.
2. A legyakrabban használt Taylor-sorok a következők:
természetesen az utolsónál a z=1 pont 1 sugarú nyílt környezetében értelmezett logaritmusról van szó.
3. Mint minden hatványsor ez is egyenletesen konvergál az összegfüggvényéhez, így tagonként deriválható és integrálható.
Egész kitevőjű hatványsorok, Laurent-sor
Definíció. Ha adott a számra és (cn)n∈Z komplex számok komplex számokra a
függvénysort egész kitevőjű hatványsornak, vagy Laurent-sornak nevezzük. Egy ilyen sor összegfüggvénye:
Ugyanúgy, ahogy minden nemnegatív kitevőjű hatványsor egyenlő a saját Taylor-sorával, így az ilyen sorokat egyszerűen csak Laurent-sornak hívjuk, függetelenül attól, hogy a Laurent-sor együtthatóit egy függvény értékeiből számoljuk ki.
Ahogy a Taylor-sorfejtésben nagyon hasznos a mértani sor összegképlete (és konvergenciafeltétele), úgy ez a Laurent-soroknál is jól alkalmazható:
Példa. Mely pontok körül fejthető egész kötevőjű hatványsorba a
függvény és mik a konvergenciatartományok? Megoldás.
1) z ≠ 0-ra reguláris, így minden z0 ≠ 0-ra Taylor-sorba fejthető legalább is a z0 egy olyan környzetében, mely a 0-t mint szingularitást nem tartalmazza (hisz tudjuk: hatványsor konvergenciatartománya körlap). Ez a sor:
A sugara 1, hisz |(-1)||z-z0|<1 kell, ami ugyanaz, mint |z-z0|<1. Persze, ha |z0| < 1, akkor a sugár, maga a |z0|, hisz a 0-t nem állítja elő a sor.
2) z0 ≠ 0-ra a Laurent-sora. Most a z − z0-nak a mértani sorrá alakítás után a nevezőbe kell kerülnie:
Ennek a sorfejtésnek akkor van jelentőssége, amikor olyan pont körüli sorral akarunk egy z számot előállítani, melynek minden z-t tartalmazó gömbi környzete tartalmazza a 0-t is.
Konvergenciaköre a
egyenlőtlenségnek eleget tévő z-k.
3) z = 0-ban is van Laurent-sora, éspedig önmaga:
Ennek a sugarai R-=0, mert a (...0,0,1) sorozat n-edik gyökeinek limszupja 0, és R-=+∞, mert a (0,0,0,0,0,...) sorozat n-edik gyökeinek limszupja 0 és "reciproka" + végtelen. (Ez egyben a ∞ körüli Laurent-sor, melynek csak reguláris része van.)
Konvergenciatartomány
Laurent-sornál a konvergenciatartomány egy körgyűrű, melynek sugarait az együtthatókból a Cauchy--Hadamard-tételhez hasonló módon számolható, éspedig:
Ez a kijelentés könnyen igazolható a Cauchy-féle gyökkritériummal, sőt a Cauchy--Hadamard-tétel bizonyítását felidézve szinte magától értetődik.
Reguláris- és főrész
A Laurent-sor
részét a sor főrészének, a
részét a sor reguláris részének nevezzük.
Laurent-sorfejtés
Tétel. -- A Laurent-sor tétele -- Ha az f: C 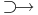 C és a ∈ C szám és 0 ≤ r < R ≤ +∞ olyan sugarak, hogy f az
C és a ∈ C szám és 0 ≤ r < R ≤ +∞ olyan sugarak, hogy f az
nyílt körgyűrűben reguláris, akkor egyértelműen léteznek olyan (cn)n∈Z komplex számok, éspedig tetszőleges a T-ben haladó az a-t egyszer pozitív irányban körbehurkoló G görbére:
hogy a
függvénysor konvergens T-ben és minden z ∈ T számra:
Bizonyítás. f-et most nem tudjuk előállítani a Cauchy-integrálformulával, mint a Taylor-sor esetén, mert az a pontban esetleg a függvény nem reguláris. De előállíthatjuk két hasonló formula különbségeként.
Rögzítsük egy tetszőlegesen választott z ∈ T-t. Legyenek k1 és k2 két a középpontú, T-ben haladó, pozitívan irányított kör, úgy, hogy z a k1 és k2 körök közötti nyílt tartományba essen. Ezekből a körökből és az őket elválasztó gyűrűt sugárirányban befelé átmetsző s szakaszból elkészítünk egy olyan zárt görbét, melyre már alkalmazható az integrálformula. Tekintsük úgy, hogy k1 kezdő és végpontja az s kezdőpontja, k2 kezdő és végpontja pedig az s végpontja. Legyen
itt (-s) az s-sel ellenkező irányítású szakaszt jelzi. Ekkor Γ a z-t egy reguláris tartományban hurkolja egyszer, pozitívan körbe, így a Cauchy-integrálformulával:
Node, ebben az integálban az s íven kétszer oda-vissza végezzük el az integrálást, így az erre vett integrál eltűnik. Másrészt a (-k2)-n vett integrál ellenkezője a 'k2-vettének, így végülis:
Hangsúlyozzuk, hogy z és a most konstansok, így a
az értelmezési tartományán analitikus függvény. Ennek -- szikásos módon a mértani sor összegére vonatkozó képlet segítségével -- elvégezhetjük az a középpontú, valamilyen körön belüli hatványsorba fejtését. Természetesen a |w-a| < |z-a| feltételt meg kell követelnünk, hiszen hatványsor konvergenciakörében nem lehet benne a z szakadási pont. Tegyük fel tehát, hogy |w-a| < |z-a|. Ekkor:
Ezzel megvan a sorfejtés minden együtthatója, ugyanis 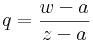 -ra kell alkalmazni a mértani sor formuláját:
-ra kell alkalmazni a mértani sor formuláját:
1) Világos, hogy ezt a sorfejtést csak a k2-re vonatkozó integrálban használhatjuk fel, mert ott lesz a q < 1 (ill. a w mindig közelebb a-hoz mint z-hez). Ezt az integrált tehát:
az integrál felcserélhető a szummával és a w-től független tagok kihozhatók az integrál elé, ezért
Ekkor egy konvergens, negatív kitevőjű hatványsort kaptunk, melynek csak főrésze van, de érdekes módon nem a középponttal és w-re, hanem a középponttal és z-ra. Ez pont a kívánt sorfejtés, melyet érdemes átindexelni úgy, hogy a szummázás -1-től induljon és -∞-ig menjen:
Már csak azt kell megmagyaráznunk, hogy a k2 helyére most már minden olyan G görbére felírható, mely az a-t pozitívan öleli körbe egyszer és a regularitási tartományban halad. Valóban, a képletbeli integrál már független az 1/(w-z) sorfejtési szituációjától és minden olyan G görbére áttranszformálható melyek folytonosan áttranszformálható k2-be. Ez a T körgyűrű összes a tételi állításban megadott görbéjére áll.
2) Most már az előző számolásból sejthető, hogy a Laurent-sor reguláris része akkor jön ki, ha az 1/(w-z) reciprokfüggvényt a az a körül nem pozitív, hanem negatív kitevőjű hatványsorba, fejtjük -- mint az első példában. Ezt a |w-a| > |z-a| feltétellel tehetjük csak meg, hisz ilyen sor konvergenciatartománya körgyűrű és a z szinguláris pontot nem tartalmazhatja:
Ez a sor valóban akkor konvergens, ha |w-a| > |z-a|. Ezzel az előző pomt számolását elvégezve az f(z)-t előállító Laurent-sor reguláris részét kapjuk. QED
Példa. Adjuk meg az
függvény azon 0 körüli Laurent-sorát, mely előállítja az 1-et! Azt is adjuk meg, mely a -3-t állítja elő!
Megoldás. -2i szinguláris hely. Ha a=0, akkor a z=1-et a 0 körüli Taylor-sor állítja elő, mert |0-1| < |0 - (-2i)|. Persze ezt is a m.s-ral adjuk meg:
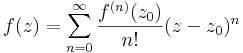
![R=\frac{1}{\limsup\limits_{n}\sqrt[n]{|a_n|}}\,](/upload/math/c/d/5/cd5d9fa4a84a6fe41527819693d07b1c.png)
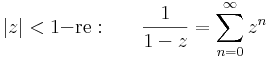
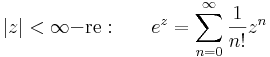
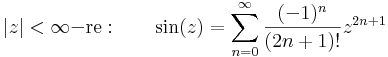
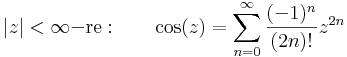
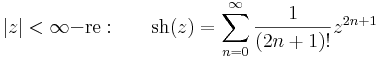
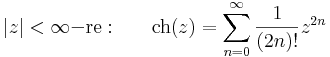
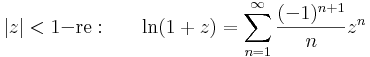
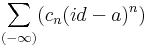
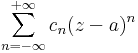
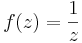
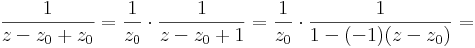
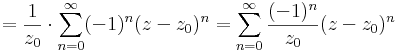
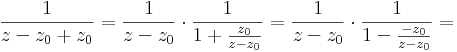
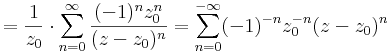
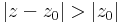
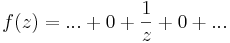
![R_+=\frac{1}{\limsup\limits_{n>0}\sqrt[n]{|c_n|}}\,](/upload/math/3/e/8/3e85834acf8b35a315b5d1921e8cb1f6.png)
![R_-=\limsup\limits_{n<0}\sqrt[n]{|c_n|}\,](/upload/math/c/f/7/cf758993102d05ada875ba223e7128d4.png)