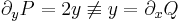Matematika A3a 2009/10. gyakorlat

Típusok és módszerek

1. Elsőrendű közönséges nemlineáris --> szeparábilis (ill. homogén fokszámú) vagy egzaktá tehető
2. Elsőrendű lineáris --> hom. ált. + inh. part.
   1. Elsőrendű lineáris homogén --> szeparábilis
   2. Elsőrendű lineáris inhomogén --> állandók variálása
3. Másodrendű hiányos --> 3 eset (g(x) hiányzik, y hiányzik, y' hiányzik)
4. Másodrendű állandóegyütthatójú lineáris
   1. --> próbafüggvény
   2. --> Laplace
   3. egyenletredszert Laplace-szal

Feladatok

1. Oldjuk meg az

$(x^2+y^2+x)+y'xy=0\,$

egyenletet az y(1) = 1 kezdeti feltétel mellett!

Mo.

$\partial_yP=2y\not\equiv y=\partial_xQ\,$

Keressünk integráló szorzót!

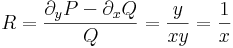$R=\frac{\partial_y P-\partial_xQ}{Q}=\frac{y}{xy}=\frac{1}{x}$ csak x-től függő. Ekkor

$\mu(x)=e^{\int R(x)\,\mathrm{d}x}$