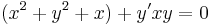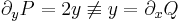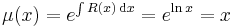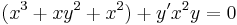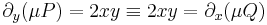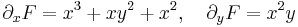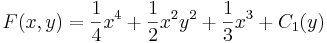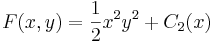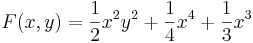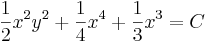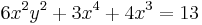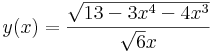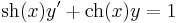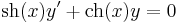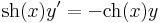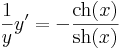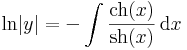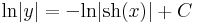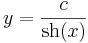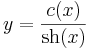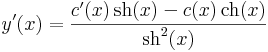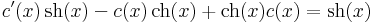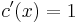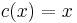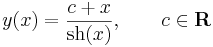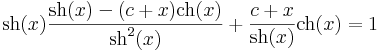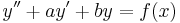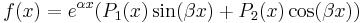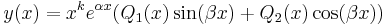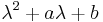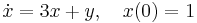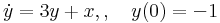Matematika A3a 2009/10. gyakorlat
Tartalomjegyzék |
Típusok és módszerek
- Elsőrendű közönséges nemlineáris --> szeparábilis (ill. homogén fokszámú) vagy egzaktá tehető
- Elsőrendű lineáris --> hom. ált. + inh. part.
- Elsőrendű lineáris homogén --> szeparábilis
- Elsőrendű lineáris inhomogén --> állandók variálása
- Másodrendű hiányos --> 3 eset (g(x) hiányzik, y hiányzik, y' hiányzik)
- Másodrendű állandóegyütthatójú lineáris
- --> próbafüggvény
- --> Laplace
- egyenletredszert Laplace-szal
Feladatok
Egzaktra visszavezethető
1. Oldjuk meg az
egyenletet az y(1) = 1 kezdeti feltétel mellett!
Mo. Nem egzakt, nem homogén fokszámú.
Keressünk integráló szorzót!
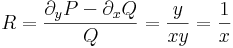 csak x-től függő.
csak x-től függő.
Ekkor
Valóban, ha
akkor
Keressünk potenciálfüggvényt! Az alábbi parciális differenciálegyenletet kell megoldanunk.
Mindkét egyenletet integráljuk aszerint a változó szerint, ami szerint a deriválás történik:
Összehasonlítva:
Valóban, ennek e megfelel. Az első integrál:
Speciálisan ebből kifejezhető az (1,1)-en áthaladó megoldás:
és
Elsőrendű függvényegyütthatós inhomogén differenciálegyenletet
2. Oldjuk meg az alábbi elsőrendű függvényegyütthatós inhomogén differenciálegyenletet!
Mo. I. A homogén egyenletet szeparálással:
II. Partikuláris megoldást keresünk az inhomogén egyenlet részére. A megoldást
alakban keressük.
az egyenlet ekkor ilyen alakú:
Tehát az inhomogén egyenlet általános megoldása:
Valóban,
Állandó együtthatójú másodrendű lineáris próbafüggvénymódszerrel
Az állandó együtthatójú másodrendű lineáris differenciálegyenlet megoldása kvadratúra nélkül megkapható, ha az
alakban az f(x) perturbáló függvény (szabad tag) a következő függvény:
Ekkor ugyanis a partikuláris megoldás kereshető az
alakban, ahol k megmutatja, hogy az α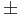 β szám hányszoros gyöke a
β szám hányszoros gyöke a
karakterisztikus polinomnak és a Q-k olyan fokszámú meghatározandó polinomok, mint a P-közül a nagyobbik fokszámú.
3.
- a)
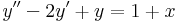
- b)
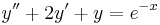
- c)
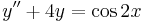
Laplace-transzformáció
Legfontosabb képletek:
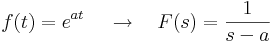 ,
, 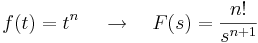 ,
, 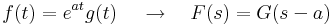
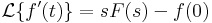 ,
, 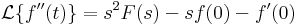
4.
- a)
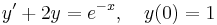
- b)