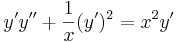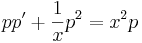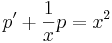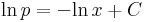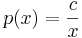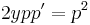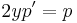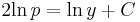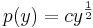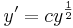Matematika A3a 2009/11. gyakorlat

Hiányos másodrendű differenciálegyenlet

1. y-ban hiányos egyenlet 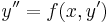$y''=f(x,y')\,$ alakú, azaz a p(x)=y' helyettesítéssel, p-ben elsőrendűvé válik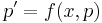 $p'=f(x,p) \,$

$y'y''+\frac{1}{x}(y')^2=x^2y'\,$

Mo.

$pp'+\frac{1}{x}p^2=x^2p\,$

$p'+\frac{1}{x}p=x^2\,$

Inhomogén lineáris. A homogén:

$\mathrm{ln}\,p=-\mathrm{ln}\,x+C$

$p(x)=\frac{c}{x}\,$

Partikuláris:

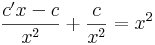
$\frac{c'x-c}{x^2}+\frac{c}{x^2}=x^2\,$

c' = x²

$c(x)=\frac{x^3}{3}\,$

$p=\frac{c}{x}+\frac{x^2}{3}$

$y=c_1\mathrm{ln}\,x+\frac{x^2}{9}+c_2$

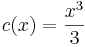
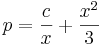
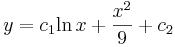
2. x-ben hiányos. Ekkor 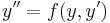$y''=f(y,y')\,$ és y'=p(y) ahol így y' ' =pp'

2yy'' = y'²

Mo.

$2ypp'=p^2\,$

$2yp'=p\,$

$2\mathrm{ln}\,p=\mathrm{ln}\,y+C$

$p(y)=cy^{\frac{1}{2}}$

$y'=cy^{\frac{1}{2}}\,$

szep.

Állandóegyütthatós

3.

$y''-2y'+5y=xe^{x}\,$