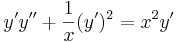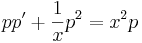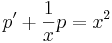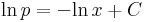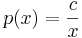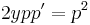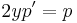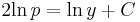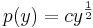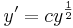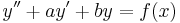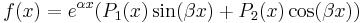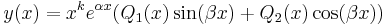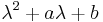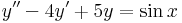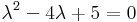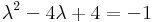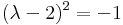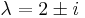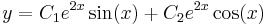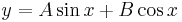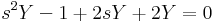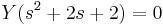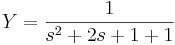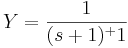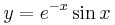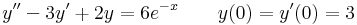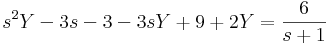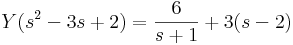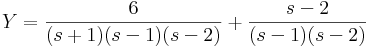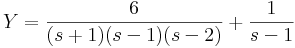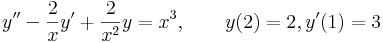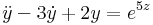Matematika A3a 2009/11. gyakorlat
A MathWikiből
Tartalomjegyzék |
Hiányos másodrendű differenciálegyenlet
1. y-ban hiányos egyenlet 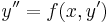 alakú, azaz a p(x)=y' helyettesítéssel, p-ben elsőrendűvé válik
alakú, azaz a p(x)=y' helyettesítéssel, p-ben elsőrendűvé válik 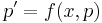
Mo.
Inhomogén lineáris. A homogén:
Partikuláris:
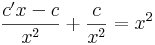
- c' = x2
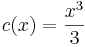
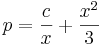
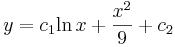
2. x-ben hiányos. Ekkor 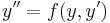 és y'=p(y) ahol így y' ' =pp'
és y'=p(y) ahol így y' ' =pp'
- 2yy'' = y'2
Mo.
szep.
Állandóegyütthatós
Homogén általános:
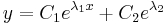 , ha λ1≠λ1 valós gyökök
, ha λ1≠λ1 valós gyökök
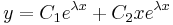 , ha λ1=λ1=λ valós gyök
, ha λ1=λ1=λ valós gyök
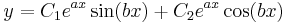 , ha a + bi ill. a − bi nemvalós gyökök.
, ha a + bi ill. a − bi nemvalós gyökök.
Ha
akkor a partikuláris megoldás kereshető az
alakban, ahol k megmutatja, hogy az α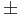 β szám hányszoros gyöke a
β szám hányszoros gyöke a
karakterisztikus polinomnak és a Q-k olyan fokszámú meghatározandó polinomok, mint a P-közül a nagyobbik fokszámú.
3.
Mo.
Hom. ált. mo.:
Inhom. part.
Laplace-transzformált
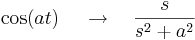
Legfontosabb képletek:
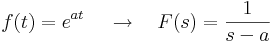 ,
, 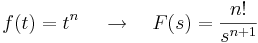 ,
, 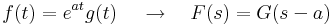
 ,
, 
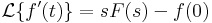 ,
, 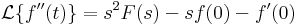
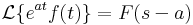
4.
Mo.
5.
Mo.
Euler-típusú
6.
Mo. Célravezet az x = ez helyettesítés (most, azaz pozitív x-ekre):