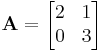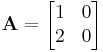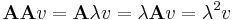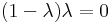Szerkesztő:Mozo/A2 gyakorló feladatok 3

1.

a) Invertálható-e és ha igen mik az A^-100 sajátértékei, ha

$\mathbf{A}=\begin{bmatrix} 2 & 1\\ 0 & 3 \end{bmatrix}$

A^-100=?

b) Mik az A¹⁰⁰ sajátértékei és sajátvektorai, ha

$\mathbf{A}=\begin{bmatrix} 1 & 0\\ 2 & 0 \end{bmatrix}$

Adjunk meg egy sajátbázisát, igazoljuk, hogy ebben az operátor diagonális. Mo. a) Invertálható, inverze:

$\mathbf{A}^{-1}=\frac{1}{6}\begin{bmatrix} 3 & -1\\ 0 & 2 \end{bmatrix}$

A sajátértékegyenlet:

$\mathbf{A}v=\lambda v\,$

de

$\mathbf{A}\mathbf{A}v=\mathbf{A}\lambda v=\lambda \mathbf{A}v=\lambda ^2v\,$

azaz ha λ sajátértéke A-nak, akkor λⁿ sajátértéke Aⁿ-nek. Ez n=-1-re 1/λ sajátértéke A^-1-nek, ha λ nem nulla.

A karakterisztikus egyenlet:

$(2-\lambda)(3-\lambda)=0\,$

azaz a sajátértékek a 2 és a 3. A -100-adiké ezek -100-adik hatványai és több nem lehet, mert a karakterisztikus polinom gyökei csak 2-en lehetnek.

b) Ez egy valódi altérbe képező operátor, mert dim Im A = 1. Espedig a képtér: {(x,2x) | x ∈ R}. A sajátértékei:

$(1-\lambda)\lambda=0\,$

0;1. Az 1-hez tartozó sajátaltér: az Im A, a 0-hoz tartozó a Ker A = {(0,y) | y ∈ R}. Sajátbázis: {(0,1),(1,2)}. A bázistrafó:

$T=\begin{bmatrix} 1 & 0\\ 2 & 1 \end{bmatrix}$

$T^{-1}AT=\begin{bmatrix} 1 & 0\\ -2 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0\\ 2 & 0 \end{bmatrix}\begin{bmatrix} 1 & 0\\ 2 & 1 \end{bmatrix}=\begin{bmatrix} 1 & 0\\ -2 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0\\ 2 & 0 \end{bmatrix}=\begin{bmatrix} 1 & 0\\ 0 & 0 \end{bmatrix}$