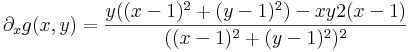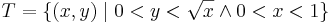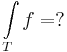Szerkesztő:Mozo/A2 gyakorló feladatok 3
1.
a) Invertálható-e és ha igen mik az A-100 sajátértékei, ha
A-100=?
b) Mik az A100 sajátértékei és sajátvektorai, ha
Adjunk meg egy sajátbázisát, igazoljuk, hogy ebben az operátor diagonális. Mo. a) Invertálható, inverze:
A sajátértékegyenlet:
de
azaz ha λ sajátértéke A-nak, akkor λn sajátértéke An-nek. Ez n=-1-re 1/λ sajátértéke A-1-nek, ha λ nem nulla.
A karakterisztikus egyenlet:
azaz a sajátértékek a 2 és a 3. A -100-adiké ezek -100-adik hatványai és több nem lehet, mert a karakterisztikus polinom gyökei csak 2-en lehetnek.
b) Ez egy valódi altérbe képező operátor, mert dim Im A = 1. Espedig a képtér: {(x,2x) | x ∈ R}. A sajátértékei:
0;1. Az 1-hez tartozó sajátaltér: az Im A, a 0-hoz tartozó a Ker A = {(0,y) | y ∈ R}. Sajátbázis: {(0,1),(1,2)}. A bázistrafó:
2.Legyen f és g a (-1,1)×(-1,1) kockán értelmezett
függvény. Folytonosak-e az origóban?
Mo.
Innen sejthető, hogy nem folytonos. Az (x,0) mentén 0, de az (x,x) mentén
 , ha (x,y)
, ha (x,y)  (0,0)
(0,0)
Másik:
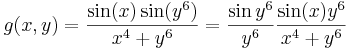
 , ha (x,y)
, ha (x,y)  (0,0)
(0,0)
3. Defferenciálhatóak-e az alábbi függvények a megadott pontban? Mi az (1,2) irányú iránymenti deriváltjuk?
Mo. A köbgyök nem diffható a 0-ban, így külön kell megnézni. A parciálisok:
innen: grad f(0,0)= [0,0].
![|\frac{\sqrt[3]{(x^2+y^2)^2}-0}{\sqrt{x^2+y^2}}|=|(x^2+y^2)^{1/6}|\to 0](/upload/math/1/6/5/1658c3612f941a4c2b74fd0ee98a2985.png) tehát az iránymenti 0.
tehát az iránymenti 0.
Másik.
4.
Mo.
5. Melyik konvergens?
a) 
b) 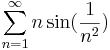
c) 
d) 
e) 
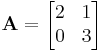
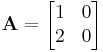


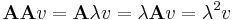

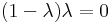




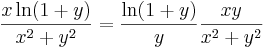
![f(x,y)=\sqrt[3]{(x^2+y^2)^2},\quad P=(0,0)](/upload/math/7/6/b/76bcd546dc12873cf5f847320614f516.png)

![f(x,0)=\sqrt[3]{x^4}, \quad f(0,y)=\sqrt[3]{y^4}](/upload/math/6/f/f/6ff560f67992511a79f7e26d6176ef64.png)