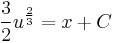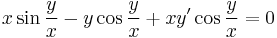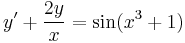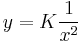Szerkesztő:Mozo/A3 gyakorló feladatok 4.

Lineáris helyettesítés

Oldja meg az alábbi egyenletet az a) y(0)=0 és b) y(0)=1 kezdeti feltételek mellett!

$y'=(\sqrt[3]{x+y})-1$

Mo. u=x+y. Innen u'=1+y':

$u'-1=(\sqrt[3]{u})-1$

$u'=(\sqrt[3]{u})$

(Itt az u=0 megoldás, azaz az y=-x megoldás)

$\int\frac{\mathrm{d}u}{\sqrt[3]{u}}=\int\mathrm{d}x$

$\frac{3}{2}u^{\frac{2}{3}}=x+C$

$\frac{3}{2}(x+y)^{\frac{2}{3}}=x+C$

A (0,0)-n nem egy megoldás halad át. Megj.: Az (y' + 1)³ − x − y = 0 egyenletnek szinguláris megoldása y=-x. y' szerinti deriváltja: 3(y' + 1)² = 0, azaz y' = − 1, azaz y=-x mentén sehol sem egyértelmű a megoldás.

Homogén fokszámú egyenlet

Oldja meg az alábbi egyenletet az a) y(π)=0 ill. b) y(2/π)=1 kezdeti feltétel mellett!

$x\sin\frac{y}{x}-y\cos\frac{y}{x}+xy'\cos\frac{y}{x}=0$

Mo. Legyen u = y / x, innen y' = u'x + u

$\sin\frac{y}{x}-\frac{y}{x}\sin\frac{y}{x}+y'\cos\frac{y}{x}=0$

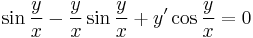
sinu − ucosu + (u'x + u)cosu = 0

sinu + u'xcosu = 0

u'xcosu = − sinu

(itt megjegyzendő, hogy az u=kπ konstansok megoldások, azaz az eredetinek az y=kπx megoldásai)

$\int-\frac{\cos u}{\sin u}\mathrm{d}u =\int\frac{\mathrm{d}x}{x}$

− ln | sinu | = ln | x | + C

$\frac{1}{|\sin u|}=K_1|x|$

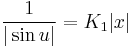
$1=Kx\sin \frac{y}{x}$ (K≠0)

Függvényegyütthatós elsőrendű lineáris d.e.

$y'+\frac{2y}{x}=\sin(x^3+1)$

Mo. Homogén megoldása. y=0 konstans megoldás.

$y'=-\frac{2y}{x}$

$\frac{dy}{y}=-2\frac{dx}{x}$

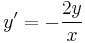
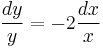
ln | y | = ln | x | ^{− 2} + C

Bolzano tétele miatt tetszőleges K valós számmal:

$y=K\frac{1}{x^2}$

ami a homogén általános megoldása.

Inhomogén part. keresése

$y(x)=K(x)\frac{1}{x^2}$

$K'(x)\frac{1}{x^2}+K(x)\frac{-2}{x^3}+K(x)\frac{2}{x^3}=\sin(x^3+1)$

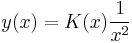
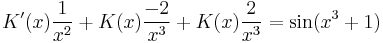
K'(x) = x²sin(x³ + 1)

$K'(x)=\frac{1}{3}3x^2\sin(x^3+1)$

$K(x)=-\frac{1}{3}\cos(x^3+1)$

$y=K\frac{1}{x^2}-\frac{1}{3}\cos(x^3+1)\frac{1}{x^2}$

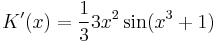
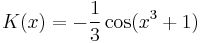
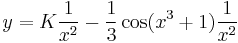
Egzaktra visszavezethető

(x² + y² + x)dx + xydy = 0, (xyy' = − x² − y² − x)

Mo. P = x² + y² + x, Q = xy, 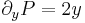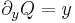$\partial_y P=2y$, $\partial_yQ=y$ azaz nem egzakt, de

$\frac{\partial_y P-\partial_yQ}{Q}\frac{2y-y}{xy}=\frac{1}{x}=R(x)$