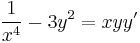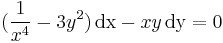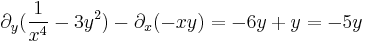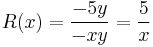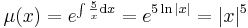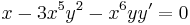Szerkesztő:Mozo/A3 gyakorló feladatok 5.
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Egzaktra visszavezethető) |
Mozo (vitalap | szerkesztései) (→Egzaktra visszavezethető) |
||
| 85. sor: | 85. sor: | ||
:<math>y=-\sqrt[6]{6e^{x^2}-7}\,</math> | :<math>y=-\sqrt[6]{6e^{x^2}-7}\,</math> | ||
===Egzaktra visszavezethető=== | ===Egzaktra visszavezethető=== | ||
| − | :<math>\ | + | :<math>\frac{1}{x^4}-3y^2=xyy'\,</math> |
MO.: | MO.: | ||
| − | :<math>(\ | + | :<math>(\frac{1}{x^4}-3y^2)\,\mathrm{dx}-xy\,\mathrm{dy}=0\,</math> |
| + | :<math>\partial_y(\frac{1}{x^4}-3y^2)-\partial_x(-xy)=-6y+y=-5y</math> | ||
| + | :<math>R(x)=\frac{-5y}{-xy}=\frac{5}{x}</math> | ||
| + | :<math>\mu(x)=e^{\int \frac{5}{x}\mathrm{d}x}=e^{5\ln|x|}=|x|^5</math> | ||
| + | Tehát <math>x^5</math> alkalmas integráló szorzó. | ||
| + | :<math>x-3x^5y^2-x^6yy'=0\,</math> | ||
A lap 2016. június 3., 22:52-kori változata
Tartalomjegyzék |
Differenciálegyenletek
Fokszámban homogén egyenletek
1. 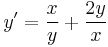
MO. u = y / x; y = ux; y' = u'x + u
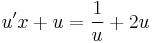
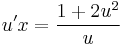

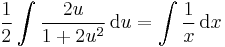
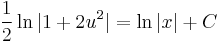 ;
; 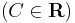
 ;
; 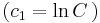
 ;
; 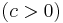
Implicit mo.:
Explicit mo.:

- Itt
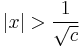
2. 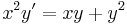
MO. y≡0 konstans mo. y=ux helyettesítéssel:
ahonnan intervallumon értelmezett megoldás esetén:
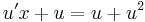
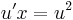
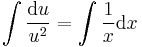
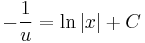 ;
; 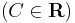
Implicit mo.:
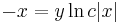 ;
; 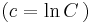 és y=0
és y=0
Explicit mo.:
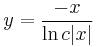 és y=0.
és y=0.
3. 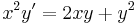
MO. y≡0 konstans mo. y=ux helyettesítéssel:
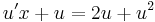
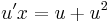
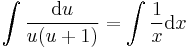
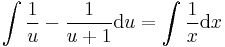
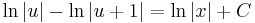 ;
; 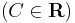
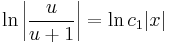 ;
; 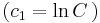
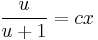 ;
; 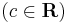
Implicit mo.:
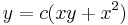 ;
; 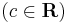
Explicit mo.:
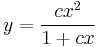 ;
; 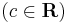
Kezdetiérték feladat
1. 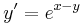 ; (y(-1)=0)
; (y(-1)=0)
MO.
Implicit ált. mo.:
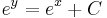 ; (
; (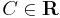 )
)
Explicit általános mo.:
Behelyettesítve az implicit ált. mo-ba:
A kezdeti feltételt kielégítő mo.:
2. 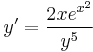 ; (y(0)=-1)
; (y(0)=-1)
MO.
Implicit ált. mo.:
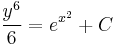 ; (
; (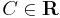 )
)
Explicit általános mo.:
![y=\pm\sqrt[6]{6e^{x^2}+6C}\,](/upload/math/3/2/3/3233e0a8d970bfb103d0ab9c3111c648.png) ; (
; (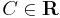 )
)
Behelyettesítve az implicit ált. mo-ba:
A kezdeti feltételt kielégítő mo.:
Egzaktra visszavezethető
MO.:
Tehát x5 alkalmas integráló szorzó.
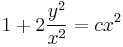
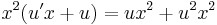
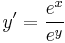
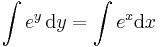
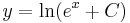
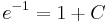
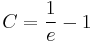
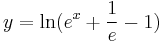
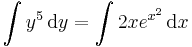

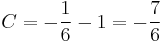
![y=-\sqrt[6]{6e^{x^2}-7}\,](/upload/math/4/d/3/4d3d122b965cc3aea8a2b9bc5c756c9c.png)