Szerkesztő:Mozo/A3 gyakorló feladatok 5.
Tartalomjegyzék |
Differenciálegyenletek
Fokszámban homogén egyenletek
1. 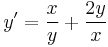
MO. u = y / x; y = ux; y' = u'x + u
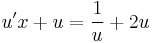
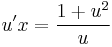
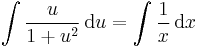
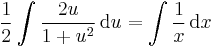
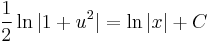 ;
; 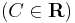
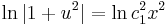 ;
; 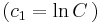
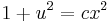 ;
; 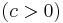
Implicit mo.:
Explicit mo.:
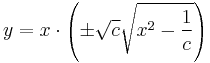
- Itt
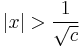
2. 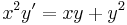
MO. y≡0 konstans mo. y=ux helyettesítéssel:
ahonnan intervallumon értelmezett megoldás esetén:
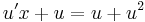
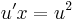
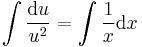
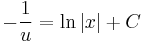 ;
; 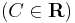
Implicit mo.:
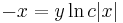 ;
; 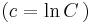 és y=0
és y=0
Explicit mo.:
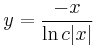 és y=0.
és y=0.
3. 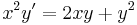
MO. y≡0 konstans mo. y=ux helyettesítéssel:
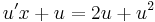
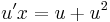
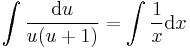
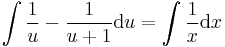
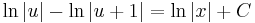 ;
; 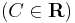
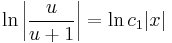 ;
; 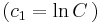
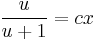 ;
; 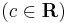
Implicit mo.:
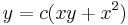 ;
; 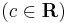
Explicit mo.:
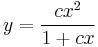 ;
; 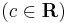
Kezdetiérték feladat
1. 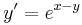 ; (y(-1)=0)
; (y(-1)=0)
MO.
Implicit ált. mo.:
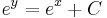 ; (
; (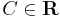 )
)
Explicit általános mo.:
Behelyettesítve az implicit ált. mo-ba:
A kezdeti feltételt kielégítő mo.:
2. 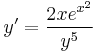 ; (y(0)=-1)
; (y(0)=-1)
MO.
Implicit ált. mo.:
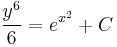 ; (
; (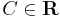 )
)
Explicit általános mo.:
![y=\pm\sqrt[6]{6e^{x^2}+6C}\,](/upload/math/3/2/3/3233e0a8d970bfb103d0ab9c3111c648.png) ; (
; (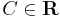 )
)
Behelyettesítve az implicit ált. mo-ba:
A kezdeti feltételt kielégítő mo.:
Egzaktra visszavezethető
Majd 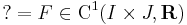
1. 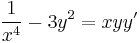
MO.:
Tehát x5 alkalmas integráló szorzó.
Innen az
egy megoldását megkeresve:
ahonnan:
És az implicit általános megoldás:
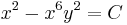 ; (
; (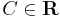 )
)
(Az explicit pedig:
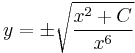 )
)
2. 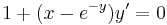
MO.:
integráló szorzó.
egy megoldását megkeresve:
ahonnan:
És az implicit általános megoldás:
 ; (
; (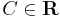 )
)
Lineáris argumentumú egyenlet
1. 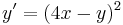
MO. u=4x-y; u'=4-y'

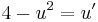 ; konstans megoldások:
; konstans megoldások: 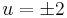
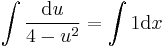 ; (ha
; (ha 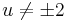 )
)
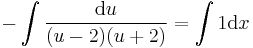
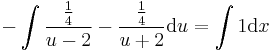
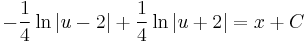
Implicit általános megoldás:
![\sqrt[4]{\left|\frac{4x-y+2}{4x-y-2}\right|}=e^{x+C}](/upload/math/a/7/d/a7d324a12a1dcfe455a1f1a7d7b08acf.png) és az szeparálással ki nem hozható két megoldás:
és az szeparálással ki nem hozható két megoldás: 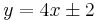
2. 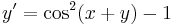
MO. u=x+y; u'=1+y'
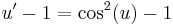 ; konstans megoldások:
; konstans megoldások: 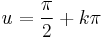
 ; (ha
; (ha 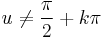 )
)
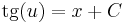
Implicit általános mo.:
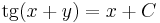 és a szeparálással ki nem hozható megoldások:
és a szeparálással ki nem hozható megoldások: 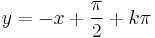
Függvényegyütthatós lineáris egyenlet
1. 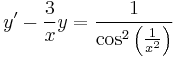
MO. I.) Homogén. y≡0 mo.
II.) Az inhomogén partikuláris megoládást
alakban keressük.
Behelyettesítés után:
így az általános mo.:
2. 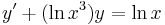
MO. I.) Homogén. y≡0 (x>0) mo.
II.) Az inhomogén partikuláris megoládást
alakban keressük. Behelyettesítés után:
így az általános mo.:
Laplace-transzformációval megoldható feladatok
1. x(0)=1; y(0)=-1 kezdeti feltétellel oldja meg az
egyenletrendszert!
MO.
Ebből kell kifejezni X-et és Y-t. Egyszerű a megoldás, ha észrevesszük, hogy ezeket összeadva:
ami minden s-re csak akkor teljesül, ha X=-Y. (De egyenletrendezéssel is megy, ha az egyik egyenletből az s-sel meg nem szorzott változót kifejezzük és a másodikbe helyettesítjük, pl. az elsőből az Y-t kifejezzük.) Innen pl. az első egyenletből:
Ezt visszatranszformálva:
És y=-x miatt:
2. y(0)=0; y'(0)=0 kezdeti feltétellel oldja meg az
egyenletet!
MO.
Innen visszatranszformálva:
Próbafüggvény módszerrel megoldható egyenletek
Homogén egyenlet megoldása:
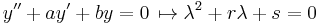 (karakterisztikus polinom)
(karakterisztikus polinom)
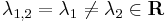 , akkor
, akkor 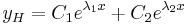 (belső rezonancia)
(belső rezonancia)
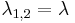 , akkor
, akkor 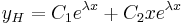
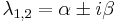 , akkor
, akkor 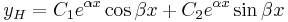
Inhomogén partikuláris alakja rezonanciák nélkül, spéci esetekben:
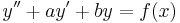 , és
, és
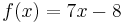 , akkor
, akkor 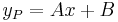
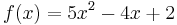 , akkor
, akkor 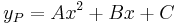
 , akkor
, akkor 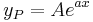
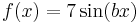 , akkor
, akkor 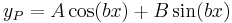
Általános (exp., trig., pol.) esetben pedig ha
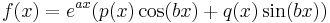 ,
,
akkor
ahol 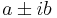 a karakterisztikus polinomnak m-szeres gyöke és deg{P}=deg{Q}=max{deg P, deg Q} polinomok (úgy értve, hogy deg 0=-∞). Tehát ha m>0, akkor külső rezonancia van.
a karakterisztikus polinomnak m-szeres gyöke és deg{P}=deg{Q}=max{deg P, deg Q} polinomok (úgy értve, hogy deg 0=-∞). Tehát ha m>0, akkor külső rezonancia van.
1. Adja meg az
egyenlet általános megoldását!
MO. 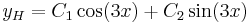 , mert
, mert 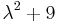 gyökei
gyökei 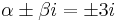
Ezt behelyettesítve az egyenletbe:
Tehát 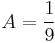 és
és 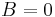 , így az általános megoldás:
, így az általános megoldás:
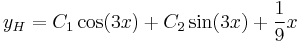 ,
,
2. (Rezonanciás feladatok)
a. 
Mo. vázlat. 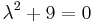 , azaz
, azaz 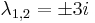 . Innen
. Innen
- yH(x) = C1cos(3x) + C2sin(3x)
Mivel
ezért a + bi = 3i egyszeres megoldása a karakterisztikus egyenletnek, m=1 és az általános P(x), Q(x) polinomok konstansok: A,B, így az inhomogén egyenlet egy partikuláris megoldása az
alakban keresendő.
b. 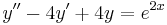
Mo. vázlat.  , azaz
, azaz 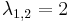 . Innen
. Innen
Mivel
ezért a = 2 kétszeres megoldása a karakterisztikus egyenletnek, és ezért m=2 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik, de P(x)=A állandó, így az inhomogén egyenlet egy partikuláris megoldása az
alakban keresendő.
c. 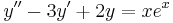
Mo. vázlat. 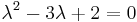 , azaz
, azaz  . Innen
. Innen
Mivel
ezért a = 1 egyszeres megoldása a karakterisztikus egyenletnek, és ezért m=1 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik (sin(0)=0), de P(x)=Ax+B elsőfokú, mert p(x)=x (hiszen cos(0)=1 és ez megmaradt), így az inhomogén egyenlet egy partikuláris megoldása az
alakban keresendő.
Komplex függvénytan
Folytonosság, határérték
1. Határozzuk meg, hogy az alábbi függvény folytonos-e?
Mo. A 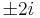 pontokon kívül a függvény folytonos függvények felhasználásával van definiálva a folytonosságot megőrző módokon, ezért
pontokon kívül a függvény folytonos függvények felhasználásával van definiálva a folytonosságot megőrző módokon, ezért 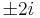 -n kívül folytonos. z = 2i-ben a függvény 0/0 alakú, ami határozatlan alak, de alakalmazható a L'Hospital szabály:
-n kívül folytonos. z = 2i-ben a függvény 0/0 alakú, ami határozatlan alak, de alakalmazható a L'Hospital szabály:
tehát a határérték létezik és a helyettesítési értékkel egyenlő, azaz 2i-ben a függvény folytonos.
z = − 2i-ben a függvény -4/0 alakú, ami a komplex függvénytanban határozott alak és ez a komplex végtelen: -4/0=∞. Tehát itt a függvény nem folytonos.
2. Hol létezik véges határértéke az alábbi függvényeknek?
- a)
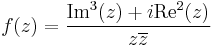
- b)
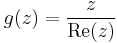
Mo. a) Legyen z = x + iy. Mivel 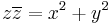 , ezért f csak a 0-ban nincs értelmezve. Itt valós és képzetes részre bontva:
, ezért f csak a 0-ban nincs értelmezve. Itt valós és képzetes részre bontva:
A sejtés, hogy a valós komponensnek van, a képzetesnek nincs határtéráke. Ezért érdemes csak a képzetest megvizsgálni, mert pontosan akkor létezik a határérték, ha mindkét komponensnek létezik.
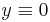 irányból
irányból 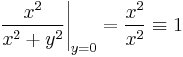
 irányból
irányból 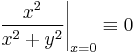
azaz a határérték nem létezhet a 0-ban. (Amúgy a valós rész határértéke létezik és 0, ugyanis rendőrelvvel:
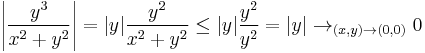 )
)
b)
Nincs értelmezve az x=0 pontokban, azaz az y tengely pontjaiban. Nemnulla y0 esetén a (0,y0) ponthoz az (x,y_0) mentén tartva y0 / x-nek végtelen a határértéke, tehát ott nem létezik. Ha y0 nulla, akkor az (x,0) mentén y/x=0, az (x,x) mentén y/x=1, azaz az origóban sincs határértéke. De mindehol máshol van, mert a határérték invariáns az alapműveletekre.
Deriválhatóság
1. Hol deriválható komplex módon és hol reguláris az alábbi függvény?
- a)
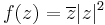
- b)**
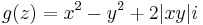
Mo. a) Legyen z = x + iy.
Ezek a parciális deriváltak mindenhol folytonosak, azaz az (u,v) pár totálisan deriválható mindenhol. Innen a Cauchy--Riemann-egyenletek:
Mivel az első, azaz 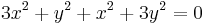 csak a 0-ban teljesül, a második pedig mindenhol, ezért a függvény pontosan a 0-ban deriválható. Ebből az is következik, hogy nincs olyan nyílt környezet, ahol minden pontban deriválható le.
csak a 0-ban teljesül, a második pedig mindenhol, ezért a függvény pontosan a 0-ban deriválható. Ebből az is következik, hogy nincs olyan nyílt környezet, ahol minden pontban deriválható le.
b) u = x2 − y2, v = 2 | xy | . Vegyük észre, hogy amikor 2|xy|=2xy egy egész nyílt környezetben, akkor g(z)=z^2, azaz ezekben az esetekben reguláris a függvény. Ez az xy>0 esetében van. Tehát csak a tengelyeken kell megvizsgálni. |xy| az origón kívül a tengelyeken parciálisan nem deriválható. Az origóban viszont CR is fennáll és totálisan is deriválhatóak a komponensek
tehát ott deriválható.
A síknegyedeken belül tehát reguláris.
2. Hol deriválható komplex módon és hol reguláris az alábbi függvény?
- a)*
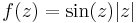
- b)
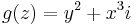
Mo. a) HF CR-egyenletekkel igazolni, hogy |z| sehol se deriválató. Azt tudjuk, hogy sin(z) mindenütt deriválható. sin(z) = 0 pontosan akkor, ha z = kπ (HF). Ezért 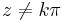 esetén, ha f(z) deriválható lenne, akkor
esetén, ha f(z) deriválható lenne, akkor
is deriválható lenne, ami tehát lehetetlen. Már csak a z = kπ pontokban kell megvizsgálni, amit definíció szerint teszünk. A különbségi hányados függvény az deriválás helyén 0/0 alakú, ezért az első tényezőre alkalmazhatjuk a L'Hospital szabályt:
ami létezik, tehát minden kπ pontban deriválható a függvény, de máshol nem, így sehol sem reguláris.
b)
Ezek a parciális deriváltak mindenhol folytonosak, azaz az (u,v) pár totálisan deriválható mindenhol. Innen a Cauchy--Riemann-egyenletek:
Azaz a függvény az
parabola mentén komplex deriválható, de sehol se reguláris, mert nincs olyan nyílt környzete, melyben mindenütt deriválható lenne.
3. (Harmonikustárs-keresés)
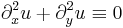 ,
,
akkor 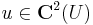 harmonikus az
harmonikus az 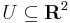 nyílton. Ha f=u+iv reguláris az U tartományon, akkor u és v harmonikus. Ha u harmonikus, az U tartományon, akkor létezik U-n v harmonikus, hogy f=u+iv reguláris. Ekkor v az u-nak egy harmonikus társa (és u az v-nek). Ha f=u+iv reguláris, akkor u,v-re teljesülnek a CR-egyenletek.
nyílton. Ha f=u+iv reguláris az U tartományon, akkor u és v harmonikus. Ha u harmonikus, az U tartományon, akkor létezik U-n v harmonikus, hogy f=u+iv reguláris. Ekkor v az u-nak egy harmonikus társa (és u az v-nek). Ha f=u+iv reguláris, akkor u,v-re teljesülnek a CR-egyenletek.
Ha létezik, akkor adjuk meg az
függvény harmonikus társát!
Mo.
tehát létezik harmonikus társa és ezt megtaláljuk az alábbiakból:
Tehát
(Hát persze, hiszen u = Re((1 + i / 2)z2))
Elemi függvények
1. Számítsa ki az
függvény valós és képzetes részét!
MO. z = x + iy
2. Oldja meg a
egyenletet!
MO.
mivel exp 2πi szerint periodikus, ezért:
3. Adja meg az
szám értékét!
MO.
Sorok
Taylor-sor:
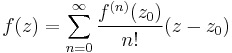
 valamely R-rel.
valamely R-rel.
Laurent-sor:
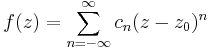
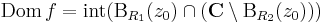 valamely R1, R2-vel.
valamely R1, R2-vel.
Az f függvénynek a ζ pont izolált szingularitása, ha f reguláris a ζ egy kipontozott környezetében, de nem reguláris ζ-ban. Izolált szingularitás körül a függvény Laurent-sor mindig lézezik ezért a sor alakja szerint osztályozzuk a szingularitásokat.
Megszüntethető, ha L.-sorban nincsenek reciprokos tagok. Ilyenkor a függvény regulárissá tehető, melynek Taylor-sora pont a Laurent-sora.
Pólusszingularitása van f-nek a ζ pontban, ha a ζ körüli Laurent-sor főrészében 1 / (z − ζ)-nak véges sok nemnulla hatványa szerepel. Ezek körzül a 1 / (z − ζ) legnagyobb kitevőjű hatványának kitevője a pólusszingularitás foka.
Lényeges szingularitása van f-nek ζ-ban, ha a ζ körüli Laurent-sorban 1 / (z − ζ)-nak végtelen sok nemnulla hatványa szerepel.
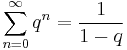 , ha | q | < 1
, ha | q | < 1
1. Igazolja, hogy az
függvénynek megszüntethető szakadása van a 0-ban! Adja meg a reguláris kiterjesztés 100. deriváltját a 0-ban!
MO.
Mivel a sorfejtés egyértelmű, ezért a z100 tag együtthatója egyértelmű, azaz egyfelől a Taylor-sorból felírva, másfelől a most megadott sorfejtésből:
2. Fejtse Laurent-sorba az
függvényt úgy, hogy a sorfejtés a 1/2 pontban előállítsa a függvényt!
a) a 0 körül,
b) az 1 körül
c) Milyen szingularitása van a -i-ben? Mennyi a reziduuma ebben?
MO. a) Ha ránézünk a becses kezeinkkel rajzolt ábrára (ugye mindenki csinált ábrát!), akkor láthatjuk, hogy a reguláris, belső körbe esik mindkét pont körül az 1/2.
tehát 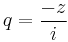 , ami |z|<1 esetén lesz konvergens sor alakú:
, ami |z|<1 esetén lesz konvergens sor alakú:
b)
tehát 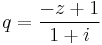 , ami
, ami 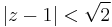 esetén lesz konvergens sor alakú:
esetén lesz konvergens sor alakú:
c)
maga a -i körüli Laurent-sor, itt a reciprokos tag együtthatója: -i, azaz ennyi a reziduum. Pólusszingularitása van itt és ennek foka 1, mert a Laurent-sor főrészében csak a reciprok szerepel.
3. Fejtse Laurent-sorba az
függvényt a 0 körül úgy, hogy a sorfejtés a 2i pontban előállítsa a függvényt! Milyen szingularitása van a 0-ban? És a -i-ben?
Mo.
Az ábrából látható, hogy a szingularitáson túli gyűrűben van 2i, ezért 1/z szerint kell sorfejteni.
tehát 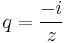 , ami |z|>1 esetén lesz konvergens sor alakú, azaz 2i ide tartozik
, ami |z|>1 esetén lesz konvergens sor alakú, azaz 2i ide tartozik
0 az f nevezőjének kétszeres gyöke, a számlálónak nem gyöke, a -i a nevezőnek egyszeres, a számlálónak nullaszoros gyöke. Tehát 0-ban másodfokú pólusa van, -i-ben elsőfokú.
4. Fejtse Laurent-sorba az
függvényt a 0 körül! Milyen szingularitása van a 0-ban?
MO.
végtelen sok tag van a főrészben, ezért a szingularitás lényeges.
Integrálás paraméterezéssel és Newton--Leibniz-formulával
ahol G paraméterezése 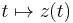 ,
, 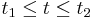 folytonosan differenciálható, f folytonos a G-t tartalmazó egy nyílt halmazon.
folytonosan differenciálható, f folytonos a G-t tartalmazó egy nyílt halmazon.
ahol F komplex deriválható és F'=f, valamint f Riemann integrálható a G mentén, G kezdőpontja z1, végpontja z2
1. Adja meg az
függvény integráláját az
a) Origó középpontú, pozitívan irányított egységkör 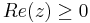 feltételt teljesítő felére!
feltételt teljesítő felére!
b) [0,2+i] szakaszra!
2. Adja meg az
függvény integráláját az
a) Origó középpontú, pozitívan irányított kétségkör 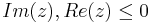 feltételt teljesítő negyedére!
b) Origó középpontú, pozitívan irányított kétségkörre!
feltételt teljesítő negyedére!
b) Origó középpontú, pozitívan irányított kétségkörre!
Integrálás Riemann-féle integráltétellel és Cauchy-féle integrálformulával
Cauchy-féle integráltétel Ha a D korlátos és zárt tartomány ∂D határa egy zárt görbével paraméterezhető és a görbe a tartománnyal kompatibilisan irányított, továbbá a D⊆U⊆C nyílt halmazon reguláris az f függvény, akkor
Riemann-féle integráltétel Ha a D korlátos és zárt tartomány ∂D határa egy zárt görbével paraméterezhető és a görbe a tartománnyal kompatibilisan irányított, továbbá a D⊆U⊆C nyílt halmazon reguláris az f függvény, kivéve a D egyetlen pontját és f korlátos, akkor
Cauchy-féle integrálformulák Ha a D korlátos és zárt, egyszeresen összefüggő tartomány G=∂D határa egy zárt görbével paraméterezhető és a görbe a tartománnyal kompatibilisan irányított, továbbá a D⊆U⊆C nyílt halmazon reguláris az f függvény és 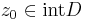 , akkor
, akkor
1.* 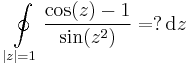
2. 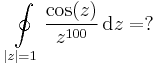
3. 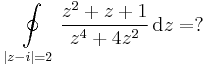
4. 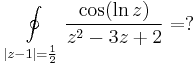
Integrálás reziduumtétellel
Reziduumtétel Ha a D korlátos és zárt, egyszeresen összefüggő tartomány G=∂D határa egy zárt görbével paraméterezhető és a görbe a tartománnyal kompatibilisan irányított, továbbá a D⊆U⊆C nyílt halmazon reguláris az f függvény kivéve a 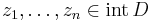 pontokban, akkor
pontokban, akkor
ahol Resf(ζ) az f függvény ζ körüli azon Laurent-sorának c − 1 együtthatója, mely a függvényt a ζ egy kipontozot környzetében állítja elő.
1.* 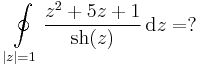
2. 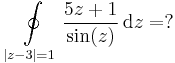
3. 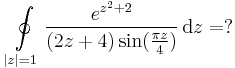
Vektoranalízis
Differenciáloperátorok
1. Hol létezik és mennyi az alábbi függvények gradiense?
- a)
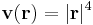
- b)
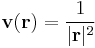
- c)
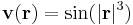
2. Hol létezik és ott mi az alábbi térbeli vektormező rotációja és divergenciája?
- a)
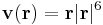
- b)
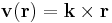 (k a z irányú egységvektor)
(k a z irányú egységvektor)
Potenciálkeresés
1. Ha van, mi az alábbi térbeli vektormező potenciálja?
2. Ha van, mi az alábbi síkbeli vektormező potenciálja?
3. Ha van, mi az alábbi függvény potenciálja?
- a)
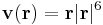
- b)
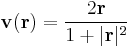
Vonalintegrál
ahol r1 = r(t1), r2 = r(t2).
ahol vt a vektormezőnek a görbe érintője irányú komponense, az integrál pedig a vektormező ívhossz szerinti integrálja.
1. Számítsuk ki az alábbi vektormezőnek az A=(1,-2,3), B=(2,1,4) végpontú egyenes szakaszra vonatkozó integrálját!
2. Számítsuk ki a v = k × r függvénynek az R sugarú, [x,y] síkbeli origó középpontú körre vonatkozó integrálját!
3. Számítsuk ki a v = k × r / |k × r|2 függvénynek az R sugarú, [x,y] síkbeli origó középpontú körre vett integrálját!
Felületi integrál
felszín integrállal a normális irányú komponensből.
1. Számítsuk ki a v vektormezőnek az r felületre vett integrálját:
2. Számítsuk ki az v = r-nek az R sugarú, M magasságú, z tengelyű hengerre vonatkozó felületi integrálját!
3. Számítsuk ki az R sugarú origó középpontú gömbnyolcad felszínére az v = r|r|3 integrálját!
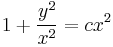
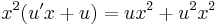
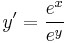
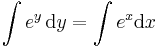
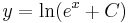
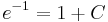
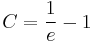
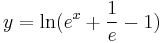
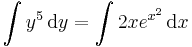
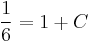
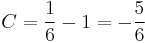
![y=-\sqrt[6]{6e^{x^2}-5}\,](/upload/math/7/1/7/71757d2adc46931ab9dfc89ee02e78af.png)
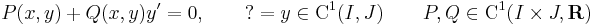
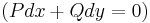
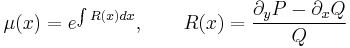
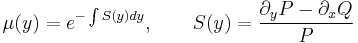
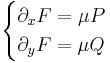
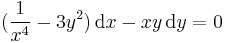
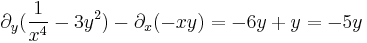
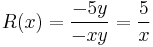
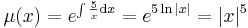
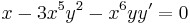
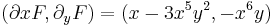
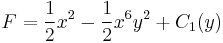
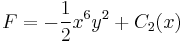
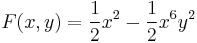
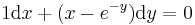
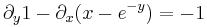
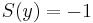
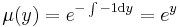
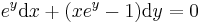
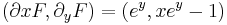
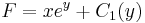
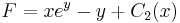
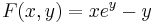
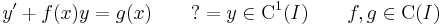
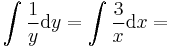
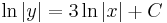
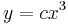
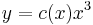
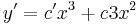
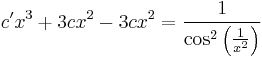
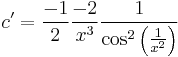
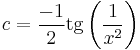
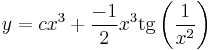
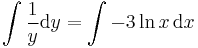
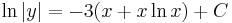
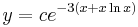
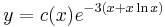
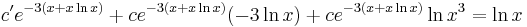
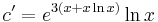
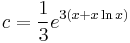
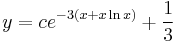
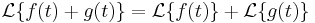
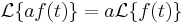
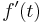
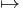
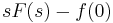
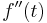
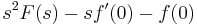
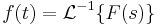
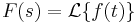
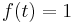
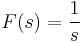
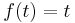
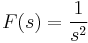
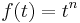
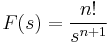
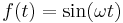
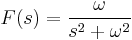
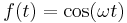
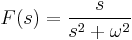
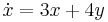
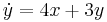
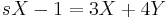
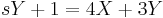

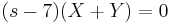
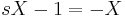
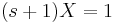
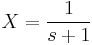
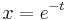
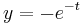
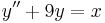
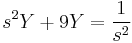
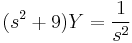
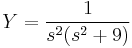
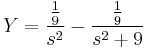
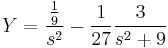

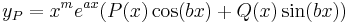
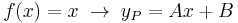
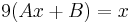
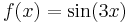
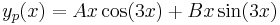
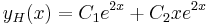
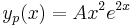
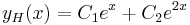
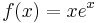
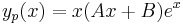
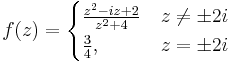
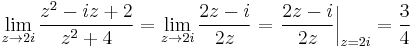
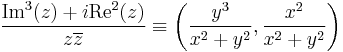
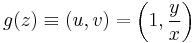
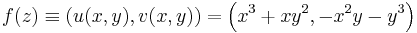
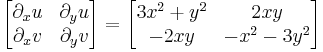
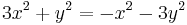
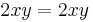
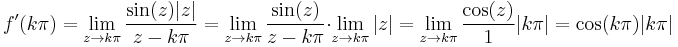
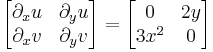
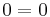
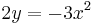
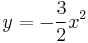
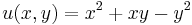
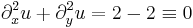
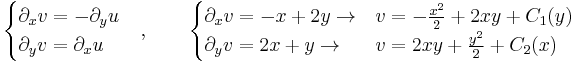
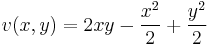
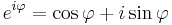
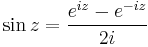
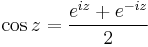
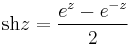
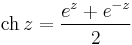
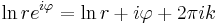
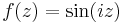
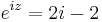
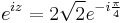
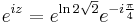
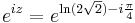
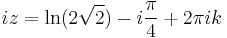
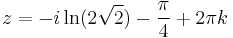
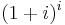
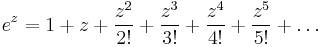
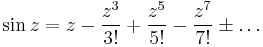
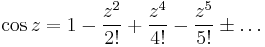
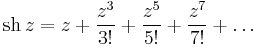
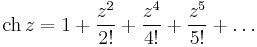
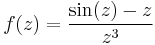
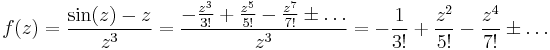
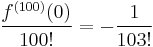
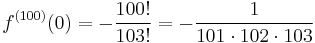
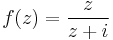
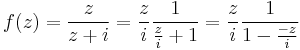
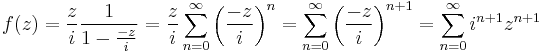
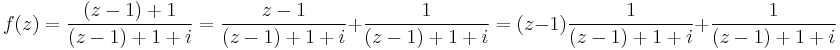
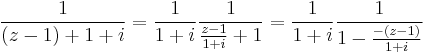
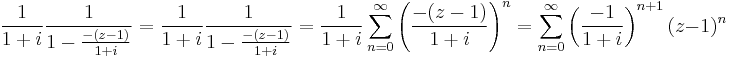
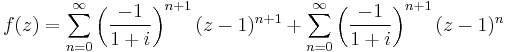
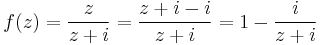
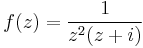
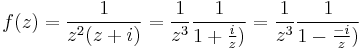
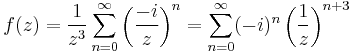
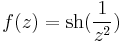
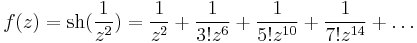
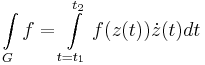
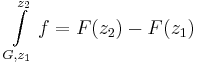
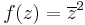
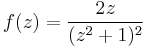
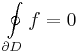
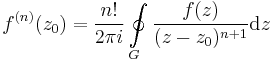
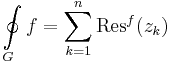
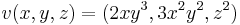
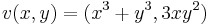
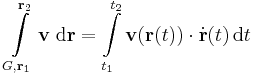
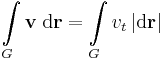
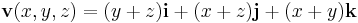
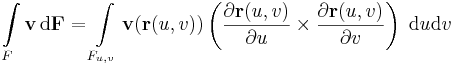
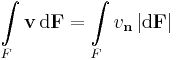
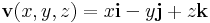
![\mathbf{r}(u,v)=(u+2v)\mathbf{i}+v\mathbf{j}+(u-v)\mathbf{k},\;u\in[0,3], \;v\in[0,1]](/upload/math/5/6/d/56dbbb3ec759a8369f2ad5aa78a072dc.png)