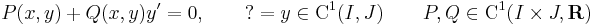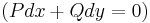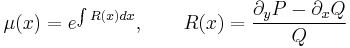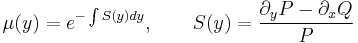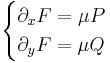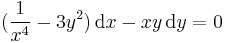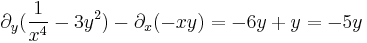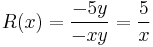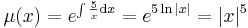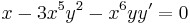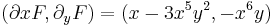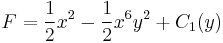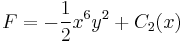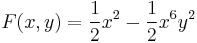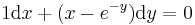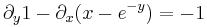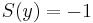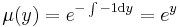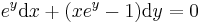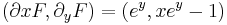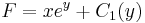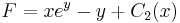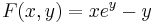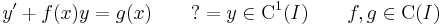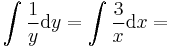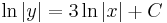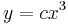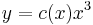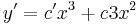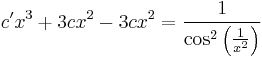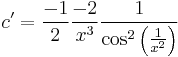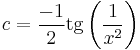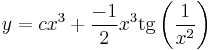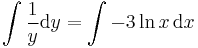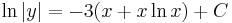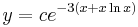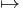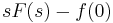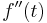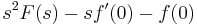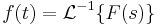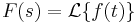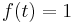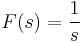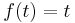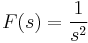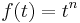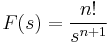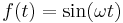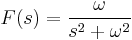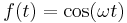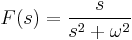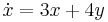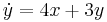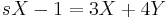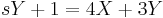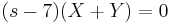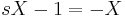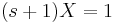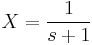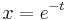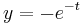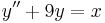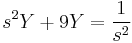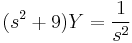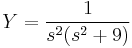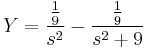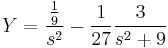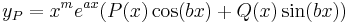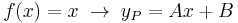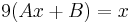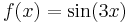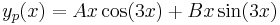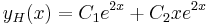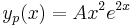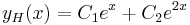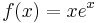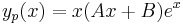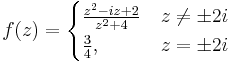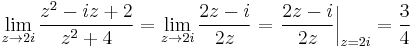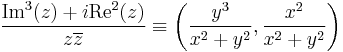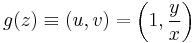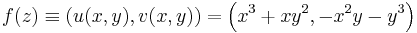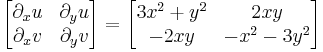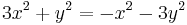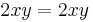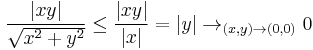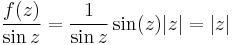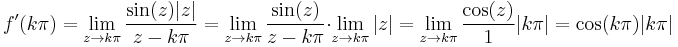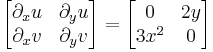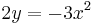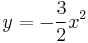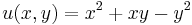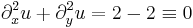Szerkesztő:Mozo/A3 gyakorló feladatok 5.
Mozo (vitalap | szerkesztései) (→Egzaktra visszavezethető) |
Mozo (vitalap | szerkesztései) |
||
| 394. sor: | 394. sor: | ||
:<math>y=-\frac{3}{2}x^2\,</math> | :<math>y=-\frac{3}{2}x^2\,</math> | ||
parabola mentén komplex deriválható, de sehol se reguláris, mert nincs olyan nyílt környzete, melyben mindenütt deriválható lenne. | parabola mentén komplex deriválható, de sehol se reguláris, mert nincs olyan nyílt környzete, melyben mindenütt deriválható lenne. | ||
| + | |||
| + | |||
| + | '''3.''' (Harmonikustárs-keresés) | ||
| + | |||
| + | :<math>\partial_x^2u+\partial_y^2u\equiv 0</math>, | ||
| + | akkor <math>u\in\mathbf{C}^2(U)</math> harmonikus <math>U\subseteq\mathbf{R}^2</math> nyílt. Ha f=u+iv reguláris az U tartományon, akkor u és v harmonikus. Ha u harmonikus, az U tartományon, akkor létezik U-n v harmonikus, hogy f=u+iv reguláris. Ekkor v az u-nak egy harmonikus társa (és u az v-nek). Ha f=u+iv reguláris, akkor u,v-re teljesülnek a CR-egyenletek. | ||
| + | |||
| + | |||
| + | Ha létezik, akkor adjuk meg az | ||
| + | :<math>u(x,y)=x^2+xy-y^2\,</math> | ||
| + | függvény harmonikus társát! | ||
| + | |||
| + | |||
| + | ''Mo.'' | ||
| + | :<math>\partial_x^2u+\partial_y^2u=2-2\equiv 0</math> | ||
| + | |||
| + | tehát létezik harmonikus társa és ezt megtaláljuk az alábbiakból: | ||
| + | |||
| + | :<math>\begin{cases}\partial_xv=-\partial_yu\\\partial_yv=\partial_xu\end{cases}</math> | ||
A lap 2016. június 4., 20:37-kori változata
Tartalomjegyzék |
Differenciálegyenletek
Fokszámban homogén egyenletek
1. 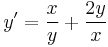
MO. u = y / x; y = ux; y' = u'x + u
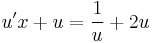
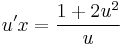

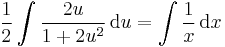
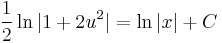 ;
; 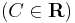
 ;
; 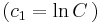
 ;
; 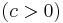
Implicit mo.:
Explicit mo.:

- Itt
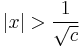
2. 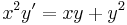
MO. y≡0 konstans mo. y=ux helyettesítéssel:
ahonnan intervallumon értelmezett megoldás esetén:
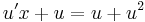
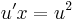
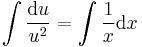
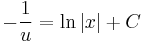 ;
; 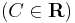
Implicit mo.:
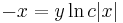 ;
; 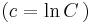 és y=0
és y=0
Explicit mo.:
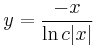 és y=0.
és y=0.
3. 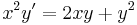
MO. y≡0 konstans mo. y=ux helyettesítéssel:
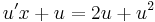
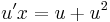
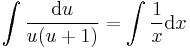
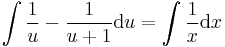
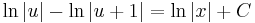 ;
; 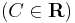
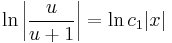 ;
; 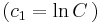
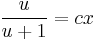 ;
; 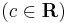
Implicit mo.:
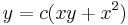 ;
; 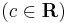
Explicit mo.:
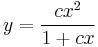 ;
; 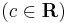
Kezdetiérték feladat
1. 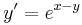 ; (y(-1)=0)
; (y(-1)=0)
MO.
Implicit ált. mo.:
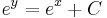 ; (
; (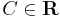 )
)
Explicit általános mo.:
Behelyettesítve az implicit ált. mo-ba:
A kezdeti feltételt kielégítő mo.:
2. 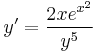 ; (y(0)=-1)
; (y(0)=-1)
MO.
Implicit ált. mo.:
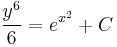 ; (
; (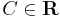 )
)
Explicit általános mo.:
![y=\pm\sqrt[6]{6e^{x^2}+6C}\,](/upload/math/3/2/3/3233e0a8d970bfb103d0ab9c3111c648.png) ; (
; (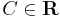 )
)
Behelyettesítve az implicit ált. mo-ba:
A kezdeti feltételt kielégítő mo.:
Egzaktra visszavezethető
Majd 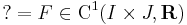
1. 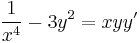
MO.:
Tehát x5 alkalmas integráló szorzó.
Innen az
egy megoldását megkeresve:
ahonnan:
És az implicit általános megoldás:
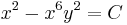 ; (
; (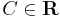 )
)
(Az explicit pedig:
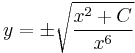 )
)
2. 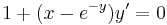
MO.:
integráló szorzó.
egy megoldását megkeresve:
ahonnan:
És az implicit általános megoldás:
 ; (
; (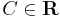 )
)
Lineáris argumentumú egyenlet
1. 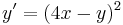
MO. u=4x-y; u'=4-y'

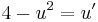 ; konstans megoldások:
; konstans megoldások: 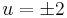
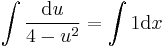 ; (ha
; (ha 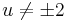 )
)
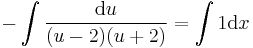
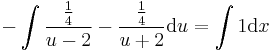
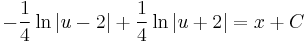
Implicit általános megoldás:
![\sqrt[4]{\left|\frac{4x-y+2}{4x-y-2}\right|}=e^{x+C}](/upload/math/a/7/d/a7d324a12a1dcfe455a1f1a7d7b08acf.png) és az szeparálással ki nem hozható két megoldás:
és az szeparálással ki nem hozható két megoldás: 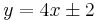
2. 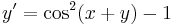
MO. u=x+y; u'=1+y'
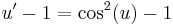 ; konstans megoldások:
; konstans megoldások: 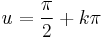
 ; (ha
; (ha 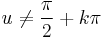 )
)
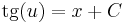
Implicit általános mo.:
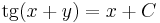 és a szeparálással ki nem hozható megoldások:
és a szeparálással ki nem hozható megoldások: 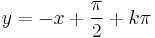
Függvényegyütthatós lineáris egyenlet
1. 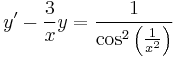
MO. I.) Homogén. y≡0 mo.
II.) Az inhomogén partikuláris megoládást
alakban keressük.
Behelyettesítés után:
így az általános mo.:
2. 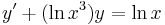
MO. I.) Homogén. y≡0 (x>0) mo.
II.) Az inhomogén partikuláris megoládást
alakban keressük. Behelyettesítés után:
így az általános mo.:
Laplace-transzformációval megoldható feladatok
1. x(0)=1; y(0)=-1 kezdeti feltétellel oldja meg az
egyenletrendszert!
MO.
Ebből kell kifejezni X-et és Y-t. Egyszerű a megoldás, ha észrevesszük, hogy ezeket összeadva:
ami minden s-re csak akkor teljesül, ha X=-Y. (De egyenletrendezéssel is megy, ha az egyik egyenletből az s-sel meg nem szorzott változót kifejezzük és a másodikbe helyettesítjük, pl. az elsőből az Y-t kifejezzük.) Innen pl. az első egyenletből:
Ezt visszatranszformálva:
És y=-x miatt:
2. y(0)=0; y'(0)=0 kezdeti feltétellel oldja meg az
egyenletet!
MO.
Innen visszatranszformálva:
Próbafüggvény módszerrel megoldható egyenletek
Homogén egyenlet megoldása:
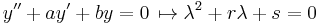 (karakterisztikus polinom)
(karakterisztikus polinom)
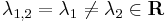 , akkor
, akkor 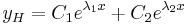 (belső rezonancia)
(belső rezonancia)
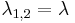 , akkor
, akkor 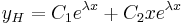
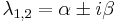 , akkor
, akkor 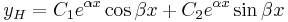
Inhomogén partikuláris alakja rezonanciák nélkül, spéci esetekben:
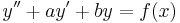 , és
, és
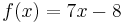 , akkor
, akkor 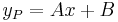
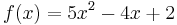 , akkor
, akkor 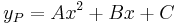
 , akkor
, akkor 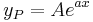
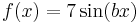 , akkor
, akkor 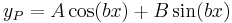
Általános (exp., trig., pol.) esetben pedig ha
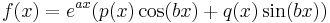 ,
,
akkor
ahol 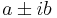 a karakterisztikus polinomnak m-szeres gyöke és deg{P}=deg{Q}=max{deg P, deg Q} polinomok (úgy értve, hogy deg 0=-∞). Tehát ha m>0, akkor külső rezonancia van.
a karakterisztikus polinomnak m-szeres gyöke és deg{P}=deg{Q}=max{deg P, deg Q} polinomok (úgy értve, hogy deg 0=-∞). Tehát ha m>0, akkor külső rezonancia van.
1. Adja meg az
egyenlet általános megoldását!
MO. 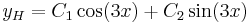 , mert
, mert 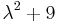 gyökei
gyökei 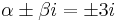
Ezt behelyettesítve az egyenletbe:
Tehát 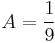 és
és 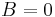 , így az általános megoldás:
, így az általános megoldás:
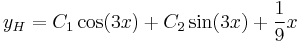 ,
,
2. (Rezonanciás feladatok)
a. 
Mo. vázlat. 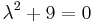 , azaz
, azaz 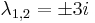 . Innen
. Innen
- yH(x) = C1cos(3x) + C2sin(3x)
Mivel
ezért a + bi = 3i egyszeres megoldása a karakterisztikus egyenletnek, m=1 és az általános P(x), Q(x) polinomok konstansok: A,B, így az inhomogén egyenlet egy partikuláris megoldása az
alakban keresendő.
b. 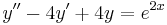
Mo. vázlat.  , azaz
, azaz 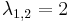 . Innen
. Innen
Mivel
ezért a = 2 kétszeres megoldása a karakterisztikus egyenletnek, és ezért m=2 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik, de P(x)=A állandó, így az inhomogén egyenlet egy partikuláris megoldása az
alakban keresendő.
c. 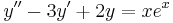
Mo. vázlat. 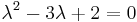 , azaz
, azaz  . Innen
. Innen
Mivel
ezért a = 1 egyszeres megoldása a karakterisztikus egyenletnek, és ezért m=1 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik (sin(0)=0), de P(x)=Ax+B elsőfokú, mert p(x)=x (hiszen cos(0)=1 és ez megmaradt), így az inhomogén egyenlet egy partikuláris megoldása az
alakban keresendő.
Komplex függvénytan
Folytonosság, határérték
1. Határozzuk meg, hogy az alábbi függvény folytonos-e?
Mo. z = 2i-ben a függvény 0/0 alakú, ami határozatlan alak, de alakalmazható a L'Hospital szabály:
tehát a határérték létezik és a helyettesítési értékkel egyenlő, azaz 2i-ben a függvény folytonos.
z = − 2i-ben a függvény -4/0 alakú, ami a komplex függvénytanban határozott alak és ez a komplex végtelen: -4/0=∞. Tehát itt a függvény nem folytonos.
2. Hol létezik véges határértéke az alábbi függvényeknek?
- a)
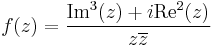
- b)
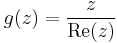
Mo. a) Legyen z = x + iy. Mivel 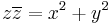 , ezért f csak a 0-ban nincs értelmezve. Itt valós és képzetes részre bontva:
, ezért f csak a 0-ban nincs értelmezve. Itt valós és képzetes részre bontva:
A sejtés, hogy a valós komponensnek van, a képzetesnek nincs határtéráke. Ezért érdemes csak a képzetest megvizsgálni, mert pontosan akkor létezik a határérték, ha mindkét komponensnek létezik.
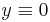 irányból
irányból 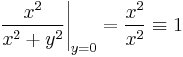
 irányból
irányból 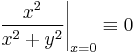
azaz a határérték nem létezhet a 0-ban. (Amúgy a valós rész határértéke létezik és 0, ugyanis rendőrelvvel:
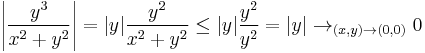 )
)
b)
Nincs értelmezve az x=0 pontokban, azaz az y tengely pontjaiban. Nemnulla y0 esetén a (0,y0) ponthoz az (x,y_0) mentén tartva y0 / x-nek végtelen a határértéke, tehát ott nem létezik. Ha y0 nulla, akkor az (x,0) mentén y/x=0, az (x,x) mentén y/x=1, azaz az origóban sincs határértéke. De mindehol máshol van, mert a határérték invariáns az alapműveletekre.
Deriválhatóság
1. Hol deriválható komplex módon és hol reguláris az alábbi függvény?
- a)
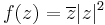
- b)**
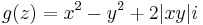
Mo. a) Legyen z = x + iy.
Ezek a parciális deriváltak mindenhol folytonosak, azaz az (u,v) pár totálisan deriválható mindenhol. Innen a Cauchy--Riemann-egyenletek:
Mivel az első, azaz 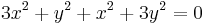 csak a 0-ban teljesül, a második pedig mindenhol, ezért a függvény pontosan a 0-ban deriválható. Ebből az is következik, hogy nincs olyan nyílt környezet, ahol minden pontban deriválható le.
csak a 0-ban teljesül, a második pedig mindenhol, ezért a függvény pontosan a 0-ban deriválható. Ebből az is következik, hogy nincs olyan nyílt környezet, ahol minden pontban deriválható le.
b) u = x2 − y2, v = 2 | xy | . Vegyük észre, hogy amikor 2|xy|=2xy egy egész nyílt környezetben, akkor g(z)=z^2, azaz ezekben az esetekben reguláris a függvény. Ez az xy>0 esetében van. Tehát csak a tengelyeken kell megvizsgálni. |xy| az origón kívül a tengelyeken parciálisan nem deriválható. Az origóban viszont CR is fennáll és totálisan is deriválhatóak a komponensek
tehát ott deriválható.
A síknegyedeken belül tehát reguláris.
2. Hol deriválható komplex módon és hol reguláris az alábbi függvény?
- a)*
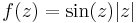
- b)
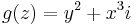
Mo. a) HF CR-egyenletekkel igazolni, hogy |z| sehol se deriválató. Azt tudjuk, hogy sin(z) mindenütt deriválható. sin(z) = 0 pontosan akkor, ha z = kπ (HF). Ezért 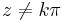 esetén, ha f(z) deriválható lenne, akkor
esetén, ha f(z) deriválható lenne, akkor
is deriválható lenne, ami tehát lehetetlen. Már csak a z = kπ pontokban kell megvizsgálni, amit definíció szerint teszünk. A különbségi hányados függvény az deriválás helyén 0/0 alakú, ezért az első tényezőre alkalmazhatjuk a L'Hospital szabályt:
ami létezik, tehát minden kπ pontban deriválható a függvény, de máshol nem, így sehol sem reguláris.
b)
Ezek a parciális deriváltak mindenhol folytonosak, azaz az (u,v) pár totálisan deriválható mindenhol. Innen a Cauchy--Riemann-egyenletek:
Azaz a függvény az
parabola mentén komplex deriválható, de sehol se reguláris, mert nincs olyan nyílt környzete, melyben mindenütt deriválható lenne.
3. (Harmonikustárs-keresés)
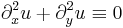 ,
,
akkor 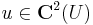 harmonikus
harmonikus 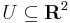 nyílt. Ha f=u+iv reguláris az U tartományon, akkor u és v harmonikus. Ha u harmonikus, az U tartományon, akkor létezik U-n v harmonikus, hogy f=u+iv reguláris. Ekkor v az u-nak egy harmonikus társa (és u az v-nek). Ha f=u+iv reguláris, akkor u,v-re teljesülnek a CR-egyenletek.
nyílt. Ha f=u+iv reguláris az U tartományon, akkor u és v harmonikus. Ha u harmonikus, az U tartományon, akkor létezik U-n v harmonikus, hogy f=u+iv reguláris. Ekkor v az u-nak egy harmonikus társa (és u az v-nek). Ha f=u+iv reguláris, akkor u,v-re teljesülnek a CR-egyenletek.
Ha létezik, akkor adjuk meg az
függvény harmonikus társát!
Mo.
tehát létezik harmonikus társa és ezt megtaláljuk az alábbiakból:
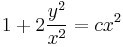
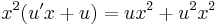
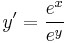
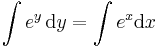
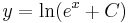
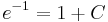
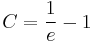
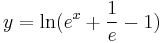
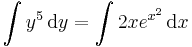

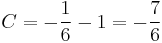
![y=-\sqrt[6]{6e^{x^2}-7}\,](/upload/math/4/d/3/4d3d122b965cc3aea8a2b9bc5c756c9c.png)