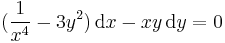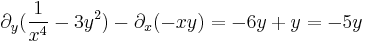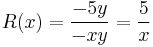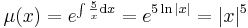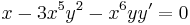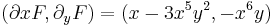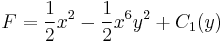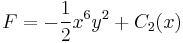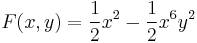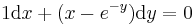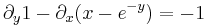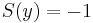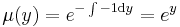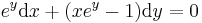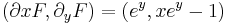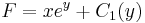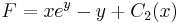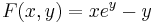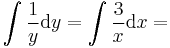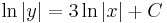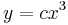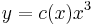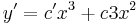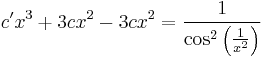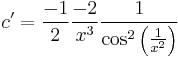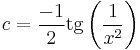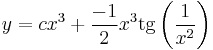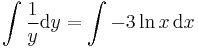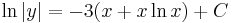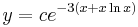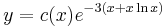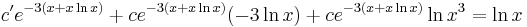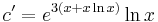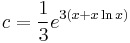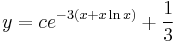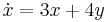Szerkesztő:Mozo/A3 gyakorló feladatok 5.
Tartalomjegyzék |
Differenciálegyenletek
Fokszámban homogén egyenletek
1. 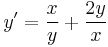
MO. u = y / x; y = ux; y' = u'x + u
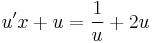
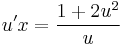

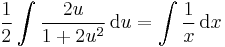
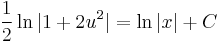 ;
; 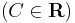
 ;
; 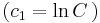
 ;
; 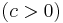
Implicit mo.:
Explicit mo.:

- Itt
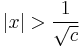
2. 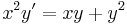
MO. y≡0 konstans mo. y=ux helyettesítéssel:
ahonnan intervallumon értelmezett megoldás esetén:
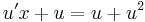
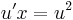
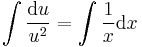
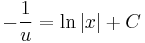 ;
; 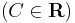
Implicit mo.:
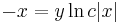 ;
; 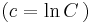 és y=0
és y=0
Explicit mo.:
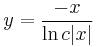 és y=0.
és y=0.
3. 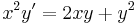
MO. y≡0 konstans mo. y=ux helyettesítéssel:
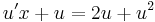
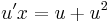
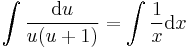
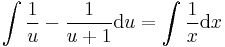
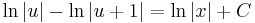 ;
; 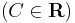
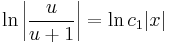 ;
; 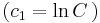
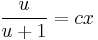 ;
; 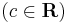
Implicit mo.:
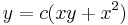 ;
; 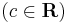
Explicit mo.:
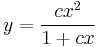 ;
; 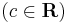
Kezdetiérték feladat
1. 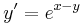 ; (y(-1)=0)
; (y(-1)=0)
MO.
Implicit ált. mo.:
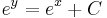 ; (
; (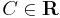 )
)
Explicit általános mo.:
Behelyettesítve az implicit ált. mo-ba:
A kezdeti feltételt kielégítő mo.:
2. 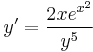 ; (y(0)=-1)
; (y(0)=-1)
MO.
Implicit ált. mo.:
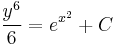 ; (
; (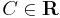 )
)
Explicit általános mo.:
![y=\pm\sqrt[6]{6e^{x^2}+6C}\,](/upload/math/3/2/3/3233e0a8d970bfb103d0ab9c3111c648.png) ; (
; (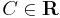 )
)
Behelyettesítve az implicit ált. mo-ba:
A kezdeti feltételt kielégítő mo.:
Egzaktra visszavezethető
1. 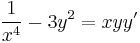
MO.:
Tehát x5 alkalmas integráló szorzó.
Innen az
egy megoldását megkeresve:
ahonnan:
És az implicit általános megoldás:
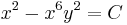 ; (
; (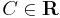 )
)
(Az explicit pedig:
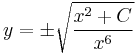 )
)
2. 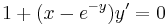
MO.:
integráló szorzó.
egy megoldását megkeresve:
ahonnan:
És az implicit általános megoldás:
 ; (
; (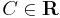 )
)
Lineáris argumentumú egyenlet
1. 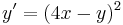
MO. u=4x-y; u'=4-y'

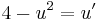 ; konstans megoldások:
; konstans megoldások: 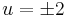
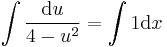 ; (ha
; (ha 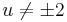 )
)
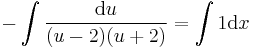
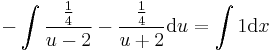
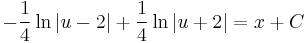
Implicit általános megoldás:
![\sqrt[4]{\left|\frac{4x-y+2}{4x-y-2}\right|}=e^{x+C}](/upload/math/a/7/d/a7d324a12a1dcfe455a1f1a7d7b08acf.png) és az szeparálással ki nem hozható két megoldás:
és az szeparálással ki nem hozható két megoldás: 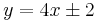
2. 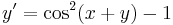
MO. u=x+y; u'=1+y'
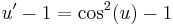 ; konstans megoldások:
; konstans megoldások: 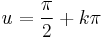
 ; (ha
; (ha 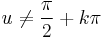 )
)
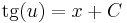
Implicit általános mo.:
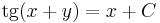 és a szeparálással ki nem hozható megoldások:
és a szeparálással ki nem hozható megoldások: 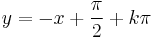
Függvényegyütthatós lineáris egyenlet
1. 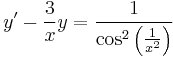
MO. I.) Homogén. y≡0 mo.
II.) Az inhomogén partikuláris megoládást
alakban keressük.
Behelyettesítés után:
így az általános mo.:
2. 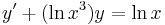
MO. I.) Homogén. y≡0 (x>0) mo.
II.) Az inhomogén partikuláris megoládást
alakban keressük. Behelyettesítés után:
így az általános mo.:
Laplace-transzformációval megoldható feladatok
1. x(0)=1; y(0)=-1 kedzeti feltétellel oldja meg az
egyenletrendszert!
MO.
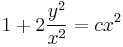
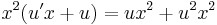
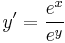
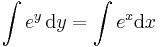
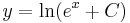
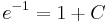
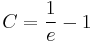
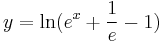
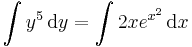

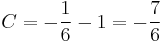
![y=-\sqrt[6]{6e^{x^2}-7}\,](/upload/math/4/d/3/4d3d122b965cc3aea8a2b9bc5c756c9c.png)