Szerkesztő:Mozo/Linalg gyakorló 3.
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) |
||
| 30. sor: | 30. sor: | ||
Megoldás: x_0+Ker(A), Ker(A)={0}, mert A invertálható: | Megoldás: x_0+Ker(A), Ker(A)={0}, mert A invertálható: | ||
| − | x_0=(1,2,1) | + | x_0=(-1,-2,-1) |
A lap 2010. március 11., 14:56-kori változata
1. Legyen L1 valódi altere az L vektortérnek (az az L1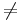
L). Igazoljuk, hogy ekkor 
.
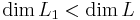Mo. Először is hivatkozunk arra, hogy ha F független rendszer, B bázis és G generátorrendszer, akkor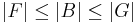 
. L1 egy B bázisa lineárisan független rendszer L-ben, így 
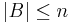, ahol 
.
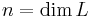Most tegyük fel indirekten, hogy |B|=n. Van olyan v vektor L-ben, ami független B-től, mert ha nem lenne, akkor B generátorrendszere lenne L-nek, amiből az következne, hogy L1=L lenne. BU{v} tehát független rendszer, azaz van L-ben n+1 elemű független rendszer. De L minden független rendszere legfeljebb csak n elemű, ami ellentmondás.
2.
Mo.
Ax=b-nek pontosan akkor van megoldása, ha r(A)=r(A|b) (itt a r(A) az A mátrix rangja). r(A) az oszlopok által kifeszített altér dimenziója.
hisz egyrészt csak háromemeletesek, másrészt van három független (1.,2.,4. oszlop). r(A)=3 pontosan akkor, ha a≠0. Ezesetben pedig valóban 1 megoldás van, mert det(A) ≠ 0.
Megoldás: x_0+Ker(A), Ker(A)={0}, mert A invertálható:
x_0=(-1,-2,-1)
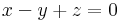
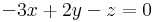
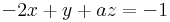
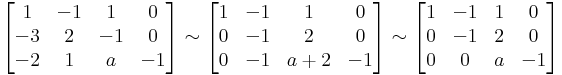
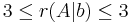
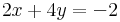
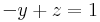
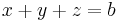
![[\mathbf{A}|\mathbf{y}]\sim\begin{bmatrix}
2 & 4 & 0 & -2\\
0 & -1 & 1 & 1\\
1 & 1 & 1 & b
\end{bmatrix}\sim\begin{bmatrix}
1 & 2 & 0 & -1\\
0 & -1 & 1 & 1\\
0 & -1 & 1 & b+1
\end{bmatrix} \sim\begin{bmatrix}
1 & 2 & 0 & -1\\
0 & -1 & 1 & 1\\
0 & 0 & 0 & b
\end{bmatrix}](/upload/math/2/d/3/2d31510649347ec9a67463a4faf92c74.png)
Megoldhatóság: b=0
Megoldások száma: végtelen, mert dimKer(A)=3-dimIm(A)=3-2=1
Megoldások: inhomogén: (-1,0,1). Ker(A)={t(-2,1,1)}
