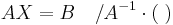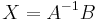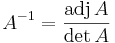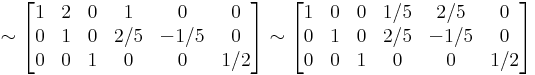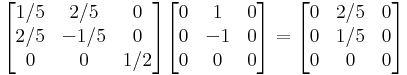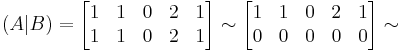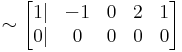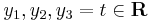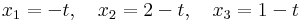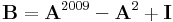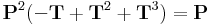Szerkesztő:Mozo/Linalg gyakorló 3.
Tartalomjegyzék |
1
Legyen L1 valódi altere az L vektortérnek (az az L1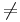 L). Igazoljuk, hogy ekkor
L). Igazoljuk, hogy ekkor 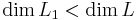 .
.
Mo. Először is hivatkozunk arra, hogy ha F független rendszer, B bázis és G generátorrendszer, akkor 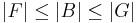 . L1 egy B bázisa lineárisan független rendszer L-ben, így
. L1 egy B bázisa lineárisan független rendszer L-ben, így 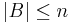 , ahol
, ahol 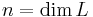 .
.
Most tegyük fel indirekten, hogy |B|=n. Van olyan v vektor L-ben, ami független B-től, mert ha nem lenne, akkor B generátorrendszere lenne L-nek, amiből az következne, hogy L1=L lenne. BU{v} tehát független rendszer, azaz van L-ben n+1 elemű független rendszer. De L minden független rendszere legfeljebb csak n elemű, ami ellentmondás.
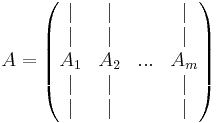
Ha tehát az A ∈ Rn×m mátrix alakja:
ahol A1, A2, ..., Am az oszlopai, akkor
ahol
jelöli az oszlopvektorok által kifeszített (generált) alteret.
Példák
1.
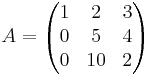 ekkor
ekkor 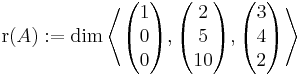
Világos, hogy az első két vektor független rendszert alkot, tehát r(A) legalább 2 (és legfeljebb 3, mert ilyen hosszúak). A kérdés, hogy a harmadik kifejezhető-e az első kettő lineáris kombinációjaként, azaz megoldható-e az
egyenletrendszer (λ1,λ2)-re? Akibővítet mártix maga az A. Ebből Gauss-eliminációval (a középső kétszeresét kivonjuk a legalsóból)
Az alsó sor így:
aminek nincs megoldása. Tehát a harmadik oszlop nem fejezhető ki az első kettő lineáris kombinációjával, így függetlenek, ergó a rang 3.
- Általánosan: ha az A n × n-es mátrixot Gauss-eliminálva háromszögmátrix jön ki, nemnulla főátlóbeli elemekkel, akkor A rangja a dimenzió: n.
2.
mert alsó sor tiviálisan teljesül, a felső kettőból pedig kifejezhető λ1, λ2, éspedig: λ2 = 4/6 = 2/3, λ1 = 5/3 (és persze az első két oszlop független, mert a másodikat a 2 nemnulla miatt sehogyan se lehet kifejezni az elsőből ennek a két nullája miatt).
2
a)
Mo.
Ax=b-nek pontosan akkor van megoldása, ha r(A)=r(A|b) (itt a r(A) az A mátrix rangja). r(A) az oszlopok által kifeszített altér dimenziója.
hisz egyrészt csak háromemeletesek, másrészt van három független (1.,2.,4. oszlop). r(A)=3 pontosan akkor, ha a≠0. Ezesetben pedig valóban 1 megoldás van, mert det(A) ≠ 0.
Megoldás: x_0+Ker(A), Ker(A)={0}, mert A invertálható:
x_0=(-1,-2,-1)
b)
Mo.
Megoldhatóság: b=0
Megoldások száma: végtelen, mert dimKer(A)=3-dimIm(A)=3-2=1
Megoldások: inhomogén: (-1,0,1). Ker(A)={t(-2,1,1)}
3
Oldjuk meg az AX=B mátrixegyenletet, ha
a)
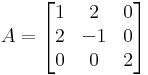 és
és
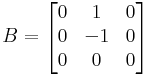
Mo. A invertálató, mert a determinánsa -2-8=-10 és ekkor a megoldás:
Az iverzet sokféleképpen lehet kiszámítani. Egyfelől az inverzmátrix képlet:
itt adj A az előjeles aldeterminánsmátrix transzponáltja. Másrészt kiszámíthatjuk Gauss--Jordan-eliminációval:
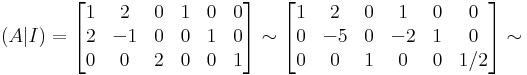
Majd megszorozzuk B-vel:
b)
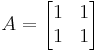 és
és
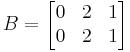 Mo. A nem invertálható. A kibővített mátrixszal:
Mo. A nem invertálható. A kibővített mátrixszal:
A második oszlopot átvisszük paraméternek:
Ha a megoldást: 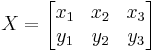 alakban írjuk föl, akkor:
alakban írjuk föl, akkor:
azaz
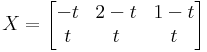
4
Milyen c-re nulla az alábbi determináns értéke?
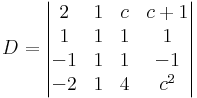 a 2. oszlop csupa 1, és a többiben is van sok egyes, tehát érdemes levonni a 2. oszlopot a többiből:
a 2. oszlop csupa 1, és a többiben is van sok egyes, tehát érdemes levonni a 2. oszlopot a többiből:
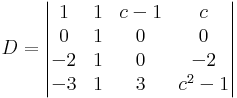 a 2. sorban egy db 1-es lett, fejtsük ki eszerint:
a 2. sorban egy db 1-es lett, fejtsük ki eszerint:
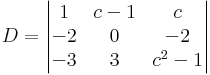 ha levonjuk az 1. oszlopot a 3-ból, akkor eltűnik a -2:
ha levonjuk az 1. oszlopot a 3-ból, akkor eltűnik a -2:
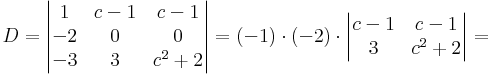
- = 2(c − 1)(c2 + 2) − 6(c − 1) = 2(c − 1)(c2 + 2 − 3) = 2(c − 1)(c2 − 1) = 0
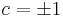
5
1. Legyen A az x+2y=0 egyenesre tükrözés operátora. Számítsa ki az
leképezés magterét és képterét!
A tükrözés, így páratlanadik hatványa önmaga, párosadik pedig az I. Emiatt B=A. 2. Legyen P az x tengelyre való vetítés, T az x tengelyre való tükrözés. Mi a P, T, P2, T2, PT, TP leképezések kép és magtere? Igazolja, hogy
Mo. Csak 3 leképezésünk van: P=P2=PT=TP, T és I. Ezeknek rendre a magtere és a képtere: {(0,t)}, {(t,0)}; {0}, R2; {0}, R2.
Az azonosság igazolása: -T+T3=0 miatt és ez előzőek miatt nyilvánvaló.
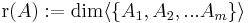
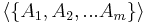
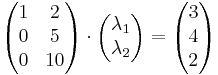
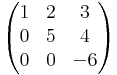
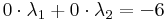
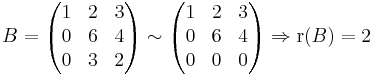
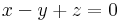
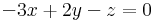
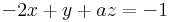
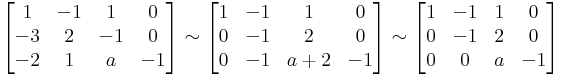
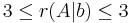
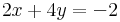
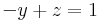
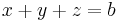
![[\mathbf{A}|\mathbf{y}]\sim\begin{bmatrix}
2 & 4 & 0 & -2\\
0 & -1 & 1 & 1\\
1 & 1 & 1 & b
\end{bmatrix}\sim\begin{bmatrix}
1 & 2 & 0 & -1\\
0 & -1 & 1 & 1\\
0 & -1 & 1 & b+1
\end{bmatrix} \sim\begin{bmatrix}
1 & 2 & 0 & -1\\
0 & -1 & 1 & 1\\
0 & 0 & 0 & b
\end{bmatrix}](/upload/math/2/d/3/2d31510649347ec9a67463a4faf92c74.png)