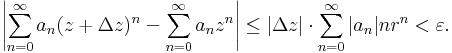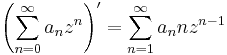Szerkesztő:Mozo/ A3 bizonyítások
Mozo (vitalap | szerkesztései) (→Cauchy-féle integráltétel) |
Mozo (vitalap | szerkesztései) (→Abel-tétel) |
||
| 3. sor: | 3. sor: | ||
==Stokes-tétel== | ==Stokes-tétel== | ||
==Abel-tétel== | ==Abel-tétel== | ||
| + | |||
| + | ===Komplex nemnegatív kitevőjű hatványsorok=== | ||
| + | |||
| + | '''Definíció''' – Legyen (''a''<sub>n</sub>) komplex számsorozat és ''z''<sub>0</sub> ∈ '''C'''. Ekkor a | ||
| + | :∑(''a''<sub>n(</sub>id<sub>'''C'''</sub>-z<sub>0</sub>)<sup>n</sup>) | ||
| + | függvénysort '''hatványsor'''nak nevezzük és összegét, az | ||
| + | :<math>z\mapsto \sum\limits_{n=0}^\infty a_n(z-z_0)^n</math> | ||
| + | hozzárendelési utasítással értelmezett, a | ||
| + | :{''z'' ∈ | ∑(''a''<sub>n</sub>(z-''z''<sub>0</sub>)<sup>n</sup>) konvergál } | ||
| + | halmazon értelmezett függvényt a hatványsor '''összegének''' nevezzük. Középpontja ''z''<sub>0</sub>, együtthatósorozata (''a''<sub>n</sub>). | ||
| + | |||
| + | A továbbiakban csak a ∑(''a''<sub>n</sub>z<sup>n</sup>) alakú, azaz a 0 körüli hatványsorokkal foglalkozunk (ezzel nem csorbítjuk az általánosságot, mert eltolással megkaphatjuk a többit is). | ||
| + | |||
| + | '''Tétel''' – ''Cauchy–Hadamard-tétel'' – Ha (''a''<sub>n</sub>) komplex számsorozat, <math>c= \limsup\limits_{n}\sqrt[n]{|a_n|}</math> és | ||
| + | :<math>R=\left\{ | ||
| + | \begin{matrix} | ||
| + | 0,& \mathrm{ha} &c=+\infty\\ | ||
| + | +\infty,& \mathrm{ha} & c=0\\ | ||
| + | \frac{1}{c},& \mathrm{ha} & 0<c<+\infty | ||
| + | \end{matrix} | ||
| + | |||
| + | \right.</math> | ||
| + | akkor ∑(''a''<sub>n</sub>z<sup>n</sup>) abszolút konvergens a B<sub>R</sub>(0) gömbön és divergens a B<sub>1/R</sub>(∞) gömbön. | ||
| + | |||
| + | ''Bizonyítás.'' Nyilvánvaló, hogy a [[User:Mozo/_A2_bizonyítások#Cauchy-féle gyökkritérium|Cauchy-féle gyökkritériumot]] kell használni a valós értékű abszolútérték-sorozatokra. Komplex sor konvergens, ha abszolút konvergens, mert igaz, hogy minden Cauchy-sorzat konvergál '''C'''-ben. | ||
| + | |||
| + | ''Megjegyzés.'' A tételbeli ''R'' sugarat a hatványsor ''konvergenciasugarának'' nevezzük. ''R''-et másként is kiszámíthajuk. Ha azt tudjuk, a '''hányadoskritérium''' alapján, hogy | ||
| + | :<math>\exists\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|}</math> | ||
| + | akkor létezik és ezzel egyenlő az n-edik gyökök sorozata is: | ||
| + | :<math>\exists\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}=\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|}=\,''\,\frac{1}{R}\,''</math> | ||
| + | ahol az idézőjel azt jelzi, hogy a konvergenciasugár lehet végtelen vagy 0 is. | ||
| + | |||
| + | '''Példa.''' Az alábbi mértani sor konvergens, ha |z|<1 és összege a szokásos: | ||
| + | :<math>\sum\limits_{n=0}^{\infty}z^n=\frac{1}{1-z}</math> | ||
| + | |||
| + | '''Példa.'''Minden ''z'' ∈ '''C'''-re konvergens az | ||
| + | :<math>\exp(z)=\sum\limits_{n=0}^{\infty}\frac{1}{n!}z^n\,</math> | ||
| + | sor, mert konvergenciasugara ∞. Ezt legegyszerűbben a hányadoskritéruimmal és a fenti megjegyzéssel állapíthatjuk meg: | ||
| + | :<math>\lim\limits_{n\to \infty}\frac{\frac{1}{(n+1)!}}{\frac{1}{n!}}=\lim\limits_{n\to \infty}\frac{n!}{(n+1)!}\to 0</math> | ||
| + | |||
| + | ===Hatványsorok összegfüggvényének folytonossága és differenciálhatósága=== | ||
| + | |||
| + | '''Tétel''' – Ha (''a''<sub>n</sub>) komplex számsorozat, akkor az ∑(''a''<sub>n</sub>z<sup>n</sup>) hatványsor összegfüggvénye folytonos a konvergenciakör belsejében. Sőt, reguláris is ott. | ||
| + | |||
| + | Emlékeztetünk arra, hogy egy függvény reguláris egy pontban, ha a pont egy környezetében mindenütt értelmezett és komplex deriválható. A tétel szerint tehát analitikus függvény reguláris. A döbbenetes azonban, hogymint később kiderül: reguláris függvény analitikus: ''f'' ∈ C<sup>ω</sup>(''z''<sub>0</sub>) akkor és csak akkr, ha ''f'' ∈ Reg(''z''<sub>0</sub>). | ||
| + | |||
| + | ''Bizonyítás.'' Legyen ''z'' a konvergenciakör egy belső pontja és Δ''z'' olyan, hogy még ''z'' + Δ''z'' is a konvergenciakör belsejébe esik. Ekkor: | ||
| + | : <math>\sum\limits_{n=0}^{\infty}a_n(z+\Delta z)^n-\sum\limits_{n=0}^{\infty}a_nz^n= | ||
| + | \sum\limits_{n=0}^{\infty}a_n((z+\Delta z)^n-z^n)=</math> | ||
| + | mert mindkét sor konvergens, ekkor algebrai azonosságokkal: | ||
| + | :<math>=\Delta z\sum\limits_{n=0}^{\infty}a_n\sum\limits_{k=0}^{n-1}\Delta z^{k}z^{n-1-k}</math> | ||
| + | vagy ha tetszik nemnulla Δ''z''-vel: | ||
| + | :<math>\frac{\sum\limits_{n=0}^{\infty}a_n(z+\Delta z)^n-\sum\limits_{n=0}^{\infty}a_nz^n}{\Delta z}=\sum\limits_{n=0}^{\infty}a_n\sum\limits_{k=0}^{n-1}\Delta z^{k}z^{n-1-k}</math> | ||
| + | a jobb oldalon álló sor konvergenciáját a gyökkritériummal láthatjuk be: | ||
| + | :<math>\left|a_n\sum\limits_{k=0}^{n-1}\Delta z^{k}z^{n-1-k}\right|\leq|a_n|\cdot n r^n</math> | ||
| + | ahol r olyan pozitív szám, hogy | ''z'' + Δ''z'' | < r < R (ez utóbbi a hatványsor konvergenciasugára). És | ||
| + | :<math>\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|\cdot n r^n}=\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|}\cdot 1 \cdot r\leq\frac{1}{R}r<1\,</math> | ||
| + | Így azt kaptuk, hogy minden olyan Δ''z''-re, melyre | ''z'' + Δ''z'' | < r, teljesül és |Δ''z''| <ε/(1+∑<sub>n</sub>|a<sub>n</sub>|nr<sup>n</sup>)=:δ | ||
| + | :<math>\left|\sum\limits_{n=0}^{\infty}a_n(z+\Delta z)^n-\sum\limits_{n=0}^{\infty}a_nz^n\right|\leq|\Delta z|\cdot \sum\limits_{n=0}^\infty|a_n|nr^n<\varepsilon.</math> | ||
| + | |||
| + | Hosszadalmasabb számolásokkal, de lényegében ugyanígy kimutatható, hogy a hatványsor összegfüggvénye komplex differenciálható is a konvergenciakör belsejében és deriváltja a formális tagonkénti deriválásal kapott sor összegfüggvényével egyenlő, tehát: | ||
| + | :<math>\left(\sum\limits_{n=0}^{\infty}a_nz^n\right)'=\sum\limits_{n=1}^{\infty}a_n n z^{n-1}</math> | ||
| + | |||
==Laurent-sorba fejtés== | ==Laurent-sorba fejtés== | ||
==Cauchy-féle integrálformulák== | ==Cauchy-féle integrálformulák== | ||
A lap 2008. december 12., 16:51-kori változata
Tartalomjegyzék |
Lineáris differenciálegyenletek
Geometriai tenzorok
Stokes-tétel
Abel-tétel
Komplex nemnegatív kitevőjű hatványsorok
Definíció – Legyen (an) komplex számsorozat és z0 ∈ C. Ekkor a
- ∑(an(idC-z0)n)
függvénysort hatványsornak nevezzük és összegét, az
hozzárendelési utasítással értelmezett, a
- {z ∈ | ∑(an(z-z0)n) konvergál }
halmazon értelmezett függvényt a hatványsor összegének nevezzük. Középpontja z0, együtthatósorozata (an).
A továbbiakban csak a ∑(anzn) alakú, azaz a 0 körüli hatványsorokkal foglalkozunk (ezzel nem csorbítjuk az általánosságot, mert eltolással megkaphatjuk a többit is).
Tétel – Cauchy–Hadamard-tétel – Ha (an) komplex számsorozat, ![c= \limsup\limits_{n}\sqrt[n]{|a_n|}](/upload/math/0/8/a/08a549d611fba6d99576372e981e8b49.png) és
és
akkor ∑(anzn) abszolút konvergens a BR(0) gömbön és divergens a B1/R(∞) gömbön.
Bizonyítás. Nyilvánvaló, hogy a Cauchy-féle gyökkritériumot kell használni a valós értékű abszolútérték-sorozatokra. Komplex sor konvergens, ha abszolút konvergens, mert igaz, hogy minden Cauchy-sorzat konvergál C-ben.
Megjegyzés. A tételbeli R sugarat a hatványsor konvergenciasugarának nevezzük. R-et másként is kiszámíthajuk. Ha azt tudjuk, a hányadoskritérium alapján, hogy
akkor létezik és ezzel egyenlő az n-edik gyökök sorozata is:
ahol az idézőjel azt jelzi, hogy a konvergenciasugár lehet végtelen vagy 0 is.
Példa. Az alábbi mértani sor konvergens, ha |z|<1 és összege a szokásos:
Példa.Minden z ∈ C-re konvergens az
sor, mert konvergenciasugara ∞. Ezt legegyszerűbben a hányadoskritéruimmal és a fenti megjegyzéssel állapíthatjuk meg:
Hatványsorok összegfüggvényének folytonossága és differenciálhatósága
Tétel – Ha (an) komplex számsorozat, akkor az ∑(anzn) hatványsor összegfüggvénye folytonos a konvergenciakör belsejében. Sőt, reguláris is ott.
Emlékeztetünk arra, hogy egy függvény reguláris egy pontban, ha a pont egy környezetében mindenütt értelmezett és komplex deriválható. A tétel szerint tehát analitikus függvény reguláris. A döbbenetes azonban, hogymint később kiderül: reguláris függvény analitikus: f ∈ Cω(z0) akkor és csak akkr, ha f ∈ Reg(z0).
Bizonyítás. Legyen z a konvergenciakör egy belső pontja és Δz olyan, hogy még z + Δz is a konvergenciakör belsejébe esik. Ekkor:
mert mindkét sor konvergens, ekkor algebrai azonosságokkal:
vagy ha tetszik nemnulla Δz-vel:
a jobb oldalon álló sor konvergenciáját a gyökkritériummal láthatjuk be:
ahol r olyan pozitív szám, hogy | z + Δz | < r < R (ez utóbbi a hatványsor konvergenciasugára). És
Így azt kaptuk, hogy minden olyan Δz-re, melyre | z + Δz | < r, teljesül és |Δz| <ε/(1+∑n|an|nrn)=:δ
Hosszadalmasabb számolásokkal, de lényegében ugyanígy kimutatható, hogy a hatványsor összegfüggvénye komplex differenciálható is a konvergenciakör belsejében és deriváltja a formális tagonkénti deriválásal kapott sor összegfüggvényével egyenlő, tehát:
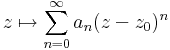
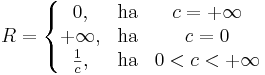
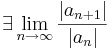
![\exists\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}=\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|}=\,''\,\frac{1}{R}\,''](/upload/math/2/1/0/210b8f12a11f0846e6103b096dee2a3d.png)



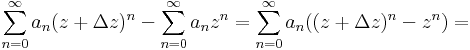
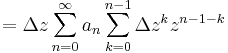
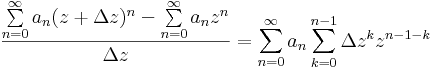
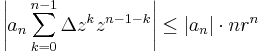
![\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|\cdot n r^n}=\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|}\cdot 1 \cdot r\leq\frac{1}{R}r<1\,](/upload/math/e/f/0/ef0679b874a4aae352293176852288ad.png)