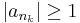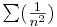Szerkesztő:Mozo/ A2 bizonyítások
Tartalomjegyzék |
Weierstrass tétele
Az alábbiakban felhasználjuk a kompaktság fogalmát (és esetleg a bizonyitas egy masik variansa a Heine–Borel-tételt).
(Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.
Heine–Borel-tétel. Veges dimenzios normalt terben korlátos és zárt halmaz kompakt.)
Tétel (Weierstrass) Valós értékű, kompakt halmazon folytonos függvény felveszi minimumát és maximumát.
- (Ha f ∈ C(Rn,R), Dom(f) kompakt, akkor sup(f), inf(f) ∈ Ran(f) )
Bizonyítás.
1) Először belátjuk, hogy kompakt halmazon folytonos függvény korlátos. Legyen ugyanis ε tetszőleges pozitív szám és f értelmezési tartománya K. A folytonosság miatt K minden u eleméhez létezik δ(u) pozitív szám, hogy f a Bδ(u) környezeten belül mindvégig az (f(u)-ε,f(u)+ε) intervallumon belül marad. Ekkor a nyílt halmazokbol allo {Bδ(u)(u) : u ∈ K} rendszer lefedi K-t, ami kompakt, azaz ebből mar véges sok is lefedi K-t. Legyen ez {Bδ(u)(u) : u ∈ F}, ahol tehát F ⊆ K véges. Ezek képei mind a (f(u)-ε,f(u)+ε) (u∈F) intervallumokban vannak, így a {(f(u)-ε,f(u)+ε) : u ∈ F} véges intervallumrendszer lefedi Ran(f)-et. Tehát f a "legmagasabb" intervallum felső határa és a "legalacsonyabb" intervallum alsó határa közé esik.
2) Belátjuk, hogy f felveszi a szuprémumát (és ugyanígy az infimumát is). Legyen S := sup(f) (azaz f értékkészletének legkisebb felső korlátja). Ekkor a g : K  R, x
R, x  S-f(x)függvény nemnegatív értékeket vesz föl. Ha f nem venné fel a szuprémumát, akkor g pozitív lenne. Ekkor értelmezhető lenne a
S-f(x)függvény nemnegatív értékeket vesz föl. Ha f nem venné fel a szuprémumát, akkor g pozitív lenne. Ekkor értelmezhető lenne a
függvény. h mert folytonos függvényekből van folytonosságot megőrző módon összetéve. Az 1) pont szerint korlátos is, ami azonban ellentmond annak, hogy S a szuprémum, mert f minden határon túl megközelíti S-et. Ugyanis minden S - 1/n számhoz létezik olyan xn ∈ K, hogy f(xn) > S - 1/n. Létezik tehát olyan (xn) K-ban haladó sorozat, melyre f(x_n) alulrúl az S-hez tart. Ám, ekkor az 1/(S-f(xn)) a +∞-hez tart, ami h korlátossága miatt lehetetlen.
Differenciálhatóság
Definíciója
Legyen f: Rn  Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn
Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn  Rm lineáris leképezés, hogy
Rm lineáris leképezés, hogy
Ekkor A egyértelmű és az f leképezés u-bent beli deriválttenzorának vagy differenciáljának nevezzük és df(u)-val vagy Df(u)-val jelöljük. Ezt a fogalmat néha teljes differenciálnak, totális differenciálnak vagy Fréchet-deriváltnak is mondjuk.
Deriváltmátrix
Vizsgáljuk mibe viszi a bázisokat df(u) komponensleképezésenként. A df(u) lineáris leképezés (e1,e2,...,en) szetenderd bázisbeli mátrixa legyen: [df(u)] = A. Világos, hogy (df(u))(x)=A x. Először vegyük az A első sorvektorát, A1-et és az e1 egységvektor mentén tartunk u-hoz: x = u + te1. A df(u)-t definiáló határértékegyenlőség ekkor a következő alakot ölti:
azaz
vagyis f első koordinátafüggvényének f1-nek az első változó szerinti parciális deriváltja az u pontban. A többi mátrixelemet ugyanígy:
amelyet Jacobi-mátrixnak nevezünk.
Lineáris, konstans és affin függvény deriváltja
Az A : Rn  Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
Ugyanis, legyen u ∈ Rn. Ekkor
c konstans függény esetén az dc(u)  0 alkalmas differenciálnak, mert
0 alkalmas differenciálnak, mert
így világos, hogy c + A alakú affin függvények is differenciálhatóak, és differenciáljuk minden pontban az az A lineáris leképezés, melynek eltolásából az affin származik. Ezt szintén behelyettesítéssel ellenőrizhetjük.
Tehát minden u ∈ Rn-re
Elégséges feltétel totális differenciálhatóságra
Tétel. Ha az f:Rn ⊃ Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható.
Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható.
Dimenziótétel
A dimenziótétel az lineáris leképezések magterének és képterének dimenziója közötti szoros (kiegészítő jellegű) kapcsolatra mutat rá. Most csak az 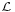 (Rn;Rm) leképezéseket vizsgáljuk (a tétel bármely végesdimenziós vektortérből tetszőleges vektortérbe menő lineáris függvényre is igaz.)
(Rn;Rm) leképezéseket vizsgáljuk (a tétel bármely végesdimenziós vektortérből tetszőleges vektortérbe menő lineáris függvényre is igaz.)
Magtér
Az A : Rn  Rm lineáris leképezés magtere:
Rm lineáris leképezés magtere:
világos, hogy ez altér. Ugyanis altér jelemzhető úgy, mint olyan részhalmaz a térben, mely zárt az összeadásra és a skalárral történő szorzásra. De Ker(A) ilyen, mert tetszőleges u, v vektorra
és
Bázisát (Rn-ben) például az A leképezés [A] mátrixának Gauss-eliminációjával és az [A]x=0 homogén egyenletrendszer megoldásával nyerhetünk (példa itt).
Képtér
Az A : Rn  Rm lineáris leképezés képtere:
Rm lineáris leképezés képtere:
világos, hogy ez altér. Ugyanis alkalmas v és u vektorokkal:
és
Bázisát (Rn-ben) például úgy nyerünk, hogy a A leképezés [A] mátrixának oszlopvektorai közül Gauss-eliminációval kiválasztjuk a legtöbb vektort tartalmazó lineárisan független rendszert (példa itt).
Dimenziótétel
Ha A: V → V' egy lineáris leképezés és V egy véges dimenziós vektortér, akkor a Ker A (az A leképezés magtere) és az Im A (az A leképezés képtere) dimenzióinak összege megegyezik a V (az A leképezés kiindulási tere) dimenziójával.
dim(KerA) + dim(ImA) = dim(V)
Bizonyítás
Legyen  a
a 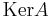 egy bázisa, és
egy bázisa, és  az
az 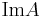 egy bázisa. A tétel bizonyításához elegendő megmutatni, hogy az
egy bázisa. A tétel bizonyításához elegendő megmutatni, hogy az 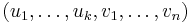 vektorrendszer a V tér egy bázisát alkotja. Ehhez be kell látni, hogy a vektorrendszer lineárisan független és egyben generátorrendszer is.
vektorrendszer a V tér egy bázisát alkotja. Ehhez be kell látni, hogy a vektorrendszer lineárisan független és egyben generátorrendszer is.
1. Lineáris függetlenség
Azt kell megmutatni, hogy a nullvektor csak triviális lineáris kombinációként állítható elő. Tegyük fel, hogy:
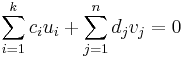
Alkalmazzuk mindkét oldalra az A lineáris leképezést:
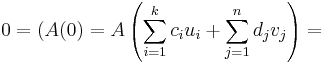
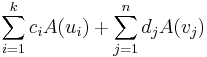
Mivel az ui vektorok a magtér bázisát alkotják, A(ui) = 0 minden i-re. Így az egyenlet a következőre egyszerűsödik:
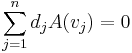
Mivel az  vektorok az képtér bázisát alkotják, lineárisan függetlenek. Ebből következik, hogy minden dj együttható nullával egyenlő. Ha ezt visszahelyettesítjük az eredeti egyenletbe, azt kapjuk, hogy:
vektorok az képtér bázisát alkotják, lineárisan függetlenek. Ebből következik, hogy minden dj együttható nullával egyenlő. Ha ezt visszahelyettesítjük az eredeti egyenletbe, azt kapjuk, hogy:
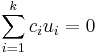
Mivel az  vektorok a magtér bázisát alkotják, ők is lineárisan függetlenek, ezért minden ci együtthatónak is nullának kell lennie. Ezzel beláttuk, hogy a
vektorok a magtér bázisát alkotják, ők is lineárisan függetlenek, ezért minden ci együtthatónak is nullának kell lennie. Ezzel beláttuk, hogy a 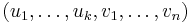 vektorrendszer lineárisan független.
vektorrendszer lineárisan független.
2. Generátorrendszer
Be kell látni, hogy a V tér bármely w vektora előáll az 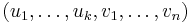 vektorok lineáris kombinációjaként.
vektorok lineáris kombinációjaként.
Mivel A(w) eleme az ImA képtérnek, és  a képtér bázisa, léteznek olyan dj skalárok, amelyekkel:
a képtér bázisa, léteznek olyan dj skalárok, amelyekkel:
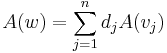
Az A leképezés linearitása miatt ez átírható a következő alakba:
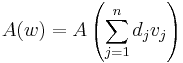
Ezt átrendezve kapjuk:
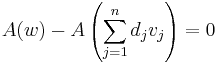 ill.
ill.
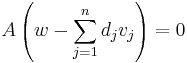
Ez azt jelenti, hogy a 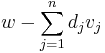 vektor eleme a KerA magtérnek. Mivel
vektor eleme a KerA magtérnek. Mivel  a magtér bázisa, léteznek olyan ci skalárok, hogy:
a magtér bázisa, léteznek olyan ci skalárok, hogy:
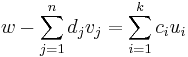
Átrendezve az egyenletet w-re:
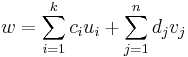
Ezzel megmutattuk, hogy bármely w vektor előáll a vizsgált vektorrendszer lineáris kombinációjaként, tehát a rendszer generátorrendszer.
Mivel a 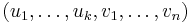 vektorrendszer lineárisan független és generátorrendszer is, ezért a V tér egy bázisát alkotja. A bázis elemszáma pedig a tér dimenzióját adja, tehát k + n = dim(V), ami a tétel állítása.
vektorrendszer lineárisan független és generátorrendszer is, ezért a V tér egy bázisát alkotja. A bázis elemszáma pedig a tér dimenzióját adja, tehát k + n = dim(V), ami a tétel állítása.
Cauchy-féle gyökkritérium
Tétel. Legyen (an) valós számsorozat, ∑(an) pedig a belőle képezett sor. Ekkor
- ha
![\mbox{ }_{\mathrm{limsup}\sqrt[n]{|a_n|}<1}](/upload/math/2/a/2/2a2c0ff510cb6780177e06a528d0b021.png) , akkor ∑(an) abszolút konvergens
, akkor ∑(an) abszolút konvergens
- ha
![\mbox{ }_{\mathrm{limsup}\sqrt[n]{|a_n|}>1}](/upload/math/f/a/7/fa7619a6b425862203c91113c4990925.png) , akkor ∑(an) divergens
, akkor ∑(an) divergens
Bizonyítás
1. Legyen
Ekkor s = limsup(cn) a lismesz szuperrior fogalmának deifíciója szerint az |an| sorozat elemeinek n-edik gyökeinek (cn) sorozatának legnagyobb sűrűsödési pontja. Sűrűsödési pont, azaz s minden környezetében van a (cn) sorozatnak végtelen sok eleme, és a legnagyobb, mert nincs nála nagyobb sűrűsödési helye (cn)-nek.
s < 1 miatt vehetünk egy q számot úgy, hogy
- s < q < 1
Ekkor s "limsupsága" miatt egy adott M természetes számot követő minden n-re:
hiszen ha lenne végtelen sok elem, melyre ez nem telhesülne, akkor lenne s nél nagyobb sűrűsödési pont is. Tehát
azaz
De a (qn) mértani sorozatból képezett sor konvergens (hisz |q|<1), így a majoráns kritérium miatt a
sor is konvergens (merthogy a szóbanforgó mértani sor majorálja). Eszerint ∑(an) abszolút konvergens.
2. A másik esetben, minthogy s = limsup(cn), van olyan részsorozata (cn)-nek melynek minden eleme 1-nél nagyobb egyenlő:
ekkor viszont
és
de a szükséges kritérium miatt ha (an) (és vele együtt az összes részsorozata) nem a 0-hoz tart, akkor ∑(an) nem konvergens, márpedig a fenti olyan részsorozata (an)-nek, mely nem tarthat a 0-hoz, így ∑(an) nem konvergens.
Megjegyzések. A bizonyításból kiderül, hogy a tétel állításának második pontjánál többet is állíthatunk. Ha ugyanis van olyan részsorozata (cn)-nek melynek minden eleme 1-nél nagyobb egyenlő, már akkor is állíthatjuk, hogy ∑(an) nem konvergens. Ám az nem igaz, hogy ha limsup(cn) 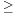 1, akkor ∑(an) nem konvergens, ellenpélda az
1, akkor ∑(an) nem konvergens, ellenpélda az
sor. Ez konverges, holott az n-edik gyökök sorozatának limesz szuperiorja 1.
Az előbb említett általános divergencia kritériumon túl azonban csak azt mondhatjuk, hogy ha limsup(cn) = 1, akkor további vizsgálatokat kell végeznünk, hogy döntésre juthassunk a konvergencia/divergencia kérdésében.
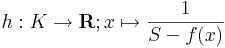
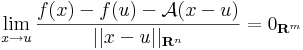
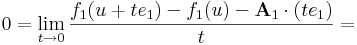
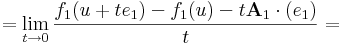
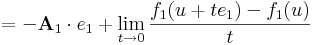
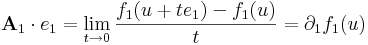
![[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix}
\partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\
\partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\
\vdots & \vdots & \ddots & \vdots \\
\partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\
\end{bmatrix}](/upload/math/b/c/8/bc8c1cf3c3d6f5032a7858552cc82a3a.png)
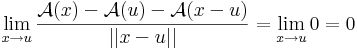
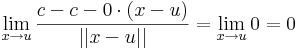

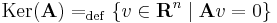
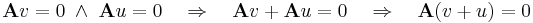
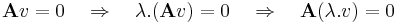
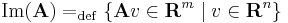


![c_n=\sqrt[n]{|a_n|}\,](/upload/math/b/3/c/b3c93c4892c869fcaa0541f02c6420cc.png)
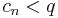
![\sqrt[n]{|a_n|} < q\,](/upload/math/8/e/d/8ed01181ef1c12da8e399eba5cdebaec.png)
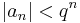
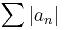
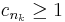
![\sqrt[n_k]{|a_{n_k}|} \geq 1\,](/upload/math/2/c/e/2ced0800302863bba53c806d141a7036.png)