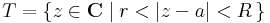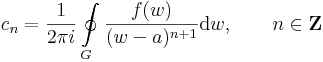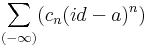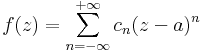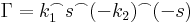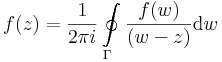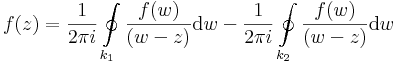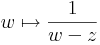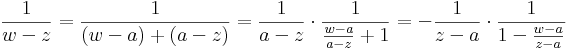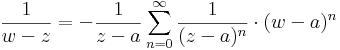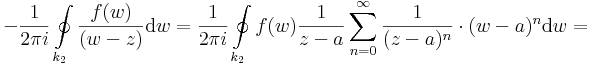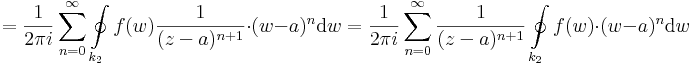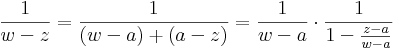Szerkesztő:Mozo/ A3 bizonyítások
Mozo (vitalap | szerkesztései) (→A tétel) |
Mozo (vitalap | szerkesztései) (→A tétel) |
||
| 89. sor: | 89. sor: | ||
De akkor a különbségi hányados minusz a majdani derivált abszolút eltérése felülbecsülhető egy nullához tartó szor korlátos függvénnyel, azaz P deriválató ''z''-ben és a deriváltja a formális tagonkénti deriválással kapott sor. | De akkor a különbségi hányados minusz a majdani derivált abszolút eltérése felülbecsülhető egy nullához tartó szor korlátos függvénnyel, azaz P deriválató ''z''-ben és a deriváltja a formális tagonkénti deriválással kapott sor. | ||
| − | De! Ez is egy hatványsor, ami ugyanilyen módon és ugyanazon a halmazon | + | De! Ez is egy hatványsor, ami ugyanilyen módon és ugyanazon a halmazon deriválható, azaz végül azt kaptuk, hogy a hatványsor nemcsak egyszer, de végtelenszer is differenciálható. Azt, hogy a Taylor-sora saját maga, a Taylor-sor létezési és egyértelműségi tételéből fog következni és mivel P előállítja saját magát, ezért persze analitikus (bár a hatványsor-előállíthatóság ezesetben a nyilvánvalónál is triviálisabb). |
==Cauchy-féle integrálformulák== | ==Cauchy-féle integrálformulák== | ||
A lap 2008. december 12., 21:07-kori változata
Tartalomjegyzék |
Lineáris differenciálegyenletek
Geometriai tenzorok
Stokes-tétel
Analitikus függvény reguláris
Komplex nemnegatív kitevőjű hatványsorok
Definíció – Legyen (an) komplex számsorozat és z0 ∈ C. Ekkor a
- ∑(an(idC-z0)n)
függvénysort hatványsornak nevezzük és összegét, az
hozzárendelési utasítással értelmezett, a
- {z ∈ | ∑(an(z-z0)n) konvergál }
halmazon értelmezett függvényt a hatványsor összegének nevezzük. Középpontja z0, együtthatósorozata (an).
A továbbiakban csak a ∑(anzn) alakú, azaz a 0 körüli hatványsorokkal foglalkozunk (ezzel nem csorbítjuk az általánosságot, mert eltolással megkaphatjuk a többit is).
Tétel – Cauchy–Hadamard-tétel – Ha (an) komplex számsorozat, ![c= \limsup\limits_{n}\sqrt[n]{|a_n|}](/upload/math/0/8/a/08a549d611fba6d99576372e981e8b49.png) és
és
akkor ∑(anzn) abszolút konvergens a BR(0) gömbön és divergens a B1/R(∞) gömbön.
Bizonyítás. Nyilvánvaló, hogy a Cauchy-féle gyökkritériumot kell használni a valós értékű abszolútérték-sorozatokra. Komplex sor konvergens, ha abszolút konvergens, mert igaz, hogy minden Cauchy-sorzat konvergál C-ben.
Megjegyzés. A tételbeli R sugarat a hatványsor konvergenciasugarának nevezzük. R-et másként is kiszámíthajuk. Ha azt tudjuk, a hányadoskritérium alapján, hogy
akkor létezik és ezzel egyenlő az n-edik gyökök sorozata is:
ahol az idézőjel azt jelzi, hogy a konvergenciasugár lehet végtelen vagy 0 is.
Példa. Az alábbi mértani sor konvergens, ha |z|<1 és összege a szokásos:
Példa.Minden z ∈ C-re konvergens az
sor, mert konvergenciasugara ∞. Ezt legegyszerűbben a hányadoskritéruimmal és a fenti megjegyzéssel állapíthatjuk meg:
A tétel
Reguláris egy függvény, ha egy nyílt halmazon komplex differenciálható. A hatványsorok ilyenek.
Tétel – Ha (an) komplex számsorozat, akkor az ∑(anzn) hatványsor összegfüggvénye komplex differenciálható a konvergenciakör belsejében.
Másként fogalmazva:
Analitikus függvény reguláris. Hiszen, ha f analitikus, akkor lokálisan hatványsor.
Bizonyítás. Ha R a konvergenciasugár, akkor legyen
és Δz olyan, hogy
A következő függvény z-beli komplex differenciálhatóságát kell belátni:
Nem árulunk zsákbamacskát, formális tagonkénti deriválással megkapható az a sor, mely ennek a függvénynek a jövendőbeli deriváltja lesz:
Világos, hogy ez utóbbi sor is konvergens a konvergenciakör belsejében. Erről a Cauchy--Hadamard-tétellel győződhetünk meg, ha |z|< r < R, akkor a konvergenciasugara:
Képezzük a különbségi hányadost és vonjuk le belőle ezt a kifejezést!
ekkor a kéttagú összeg négyzetére vonatkozó
algebrai azonossággal alakÍtjuk át a hatványt, majd amivel lehet leosztunl és amit lehet kiemelünk:
Azt kell ellenőrizni, hogy az abszolútértékbeli sor konvergens. Ezt a gyökkritériummal látjuk be. Legyen r olyan pozitív szám, hogy | z|, |Δz | < r < R. Ilyet találunk, mert a BR(0) nyílt. Ekkor
ahol (ez utóbbi a hatványsor konvergenciasugára). És
De akkor a különbségi hányados minusz a majdani derivált abszolút eltérése felülbecsülhető egy nullához tartó szor korlátos függvénnyel, azaz P deriválató z-ben és a deriváltja a formális tagonkénti deriválással kapott sor.
De! Ez is egy hatványsor, ami ugyanilyen módon és ugyanazon a halmazon deriválható, azaz végül azt kaptuk, hogy a hatványsor nemcsak egyszer, de végtelenszer is differenciálható. Azt, hogy a Taylor-sora saját maga, a Taylor-sor létezési és egyértelműségi tételéből fog következni és mivel P előállítja saját magát, ezért persze analitikus (bár a hatványsor-előállíthatóság ezesetben a nyilvánvalónál is triviálisabb).
Cauchy-féle integrálformulák
Laurent-sorba fejtés
Tétel. -- A Laurent-sor tétele -- Ha az f: C 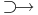 C és a ∈ C szám és 0 ≤ r < R ≤ +∞ olyan sugarak, hogy f az
C és a ∈ C szám és 0 ≤ r < R ≤ +∞ olyan sugarak, hogy f az
nyílt körgyűrűben reguláris, akkor egyértelműen léteznek olyan (cn)n∈Z komplex számok, éspedig tetszőleges a T-ben haladó az a-t egyszer pozitív irányban körbehurkoló G görbére:
hogy a
függvénysor konvergens T-ben és minden z ∈ T számra:
Bizonyítás. f-et most nem tudjuk előállítani a Cauchy-integrálformulával, mint a Taylor-sor esetén, mert az a pontban esetleg a függvény nem reguláris. De előállíthatjuk két hasonló formula különbségeként.
Rögzítsük egy tetszőlegesen választott z ∈ T-t. Legyenek k1 és k2 két a középpontú, T-ben haladó, pozitívan irányított kör, úgy, hogy z a k1 és k2 körök közötti nyílt tartományba essen. Ezekből a körökből és az őket elválasztó gyűrűt sugárirányban befelé átmetsző s szakaszból elkészítünk egy olyan zárt görbét, melyre már alkalmazható az integrálformula. Tekintsük úgy, hogy k1 kezdő és végpontja az s kezdőpontja, k2 kezdő és végpontja pedig az s végpontja. Legyen
itt (-s) az s-sel ellenkező irányítású szakaszt jelzi. Ekkor Γ a z-t egy reguláris tartományban hurkolja egyszer, pozitívan körbe, így a Cauchy-integrálformulával:
Node, ebben az integálban az s íven kétszer oda-vissza végezzük el az integrálást, így az erre vett integrál eltűnik. Másrészt a (-k2)-n vett integrál ellenkezője a 'k2-vettének, így végülis:
Hangsúlyozzuk, hogy z és a most konstansok, így a
az értelmezési tartományán analitikus függvény. Ennek -- szikásos módon a mértani sor összegére vonatkozó képlet segítségével -- elvégezhetjük az a középpontú, valamilyen körön belüli hatványsorba fejtését. Természetesen a |w-a| < |z-a| feltételt meg kell követelnünk, hiszen hatványsor konvergenciakörében nem lehet benne a z szakadási pont. Tegyük fel tehát, hogy |w-a| < |z-a|. Ekkor:
Ezzel megvan a sorfejtés minden együtthatója, ugyanis 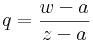 -ra kell alkalmazni a mértani sor formuláját:
-ra kell alkalmazni a mértani sor formuláját:
1) Világos, hogy ezt a sorfejtést csak a k2-re vonatkozó integrálban használhatjuk fel, mert ott lesz a q < 1 (ill. a w mindig közelebb a-hoz mint z-hez). Ezt az integrált tehát:
az integrál felcserélhető a szummával és a w-től független tagok kihozhatók az integrál elé, ezért
Ekkor egy konvergens, negatív kitevőjű hatványsort kaptunk, melynek csak főrésze van, de érdekes módon nem a középponttal és w-re, hanem a középponttal és z-ra. Ez pont a kívánt sorfejtés, melyet érdemes átindexelni úgy, hogy a szummázás -1-től induljon és -∞-ig menjen:
Már csak azt kell megmagyaráznunk, hogy a k2 helyére most már minden olyan G görbére felírható, mely az a-t pozitívan öleli körbe egyszer és a regularitási tartományban halad. Valóban, a képletbeli integrál már független az 1/(w-z) sorfejtési szituációjától és minden olyan G görbére áttranszformálható melyek folytonosan áttranszformálható k2-be. Ez a T körgyűrű összes a tételi állításban megadott görbéjére áll.
2) Most már az előző számolásból sejthető, hogy a Laurent-sor reguláris része akkor jön ki, ha az 1/(w-z) reciprokfüggvényt a az a körül nem pozitív, hanem negatív kitevőjű hatványsorba, fejtjük -- mint az első példában. Ezt a |w-a| > |z-a| feltétellel tehetjük csak meg, hisz ilyen sor konvergenciatartománya körgyűrű és a z szinguláris pontot nem tartalmazhatja:
Ez a sor valóban akkor konvergens, ha |w-a| > |z-a|. Ezzel az előző pomt számolását elvégezve az f(z)-t előállító Laurent-sor reguláris részét kapjuk. QED
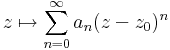
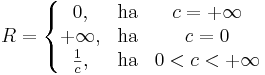
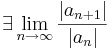
![\exists\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}=\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|}=\,''\,\frac{1}{R}\,''](/upload/math/2/1/0/210b8f12a11f0846e6103b096dee2a3d.png)



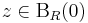


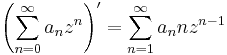
![\limsup\limits_{n\to \infty}\sqrt[n]{|a_{n}|\cdot n }=\limsup\limits_{n\to \infty}\sqrt[n]{|a_{n}|}\cdot 1=\frac{1}{R}\,](/upload/math/5/7/c/57ca0d31da52e342a251e1cc555470e9.png)
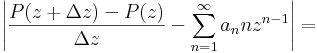

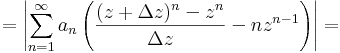
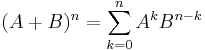


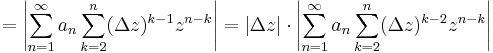

![\limsup\limits_{n\to \infty}\sqrt[n]{\frac{|a_n|\cdot (n-1) r^n}{r^2}}=\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|}\cdot \frac{1}{1} \cdot r\leq\frac{1}{R}r<1\,](/upload/math/d/a/4/da4b7320d170bffea4c4f9af93ac0d33.png)