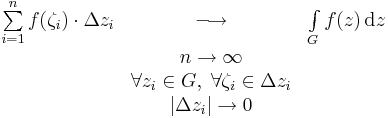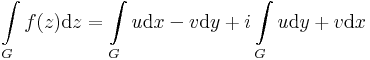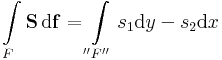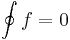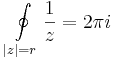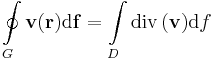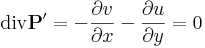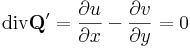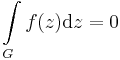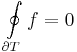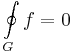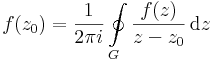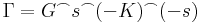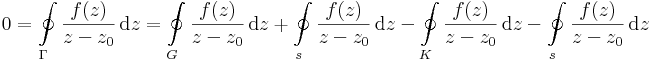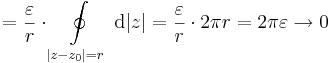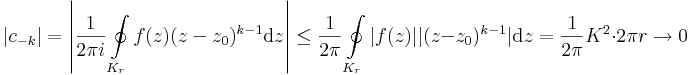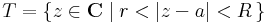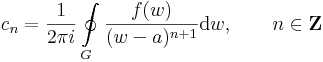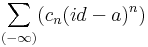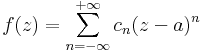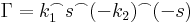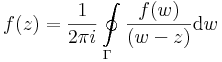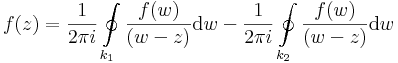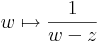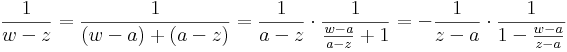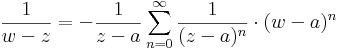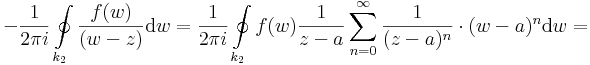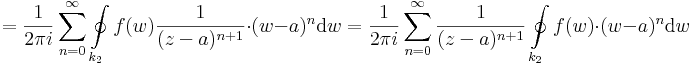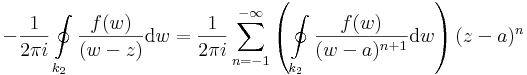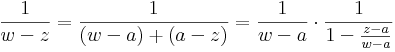Szerkesztő:Mozo/ A3 bizonyítások
Tartalomjegyzék |
Lineáris differenciálegyenletek
Inhomogén lineáris egyenlet megoldásai
Tétel. Ha V, W tetszőleges lineáris tér, A ∈ Lin(V,W) lineáris operátor, b ∈ W. Ha x0 ∈ V megoldása az Ax = b inhomogén egyenletnek, akkor az
összes megoldásainak halmaza:
Bizonyítás. 1) Ha x ∈ Ker(A), akkor Ax = 0. Ekkor
azaz ekkor x+x0 ∈ M.
2) Ha
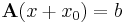 és
és 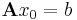
akkor
tehát x ∈ Ker(A). QED.
Megjegyzés. Tudjuk tehát akármilyen lineáris térben az inhomogén egyenlet összes megoldását, ha ismert egy megoldása. Ha tehát Ax=b lineáris differenciálegyenlet, akkor a tétel azt a szlogent fejezi ki, hogy inhomogén lineáris differenciálegyenlet általános megoldása egyenlő a homogén egyenlet általános megoldása plusz az inhomogén egyenlet egy partikuláris megoldása.
Elsőrendű inh. lin. diff. egyenlet és az állandó variálása
Állítás. Ha f: I  R folytonos függvény akkor az
R folytonos függvény akkor az
lineáris operátor a Lin(C1(I),C(I)) téren.
Bizonyítás.
Következmény. A fenti jelölésekkel, tetszőleges g folytonos függvényre, ha y0 a
differenciálegyenlet egy megoldása, akkor az egyenlet általános megoldása egyenlő a
homogén egyenlet általános megoldása plusz y0.
Példa. Oldjuk meg az
egyenletet! A partikuláris megoldást keressük az állandók variálása módszerével!
Másodrendű, áll. ehós hom. egyenlet
Tétel. Ha a,b ∈ R, akkor az
C2(I)  C(I) lineáris operátor magja kétdimenziós.
C(I) lineáris operátor magja kétdimenziós.
Megoldás. A bizonyítás két részből fog állni. Először is Laplace-transzformációval belátjuk, hogy ha dim Ker(A) legalább kettő, akkor legfeljebb 2. Másodszor pedig mutatunk 2 lineárisan független megoldást.
Bizonyítás nélkül elfogadjuk azt a tényt, hogy ha ezen egyenlet esetén egy adott pontban kezdeti értéket adunk az y-nak és az y'-nek akkor a megoldás (ha van) egyértelmű. Szemléletes képpel, ez azt jelenti, hogy ha a kezdőfázist és a sebességet megadjuk, akkor azzal a teljes hullámformát megkapjuk.
I. Legyen y1 és y2 két lineárisan független megolása az
- A y = 0
egyenletnek és legyen y ∈ Ker(A) tetszőleges. Rögzítsünk egy x0 ∈ I helyet, melyen y(x0) = u és y'(x0) = v. Elő fogjuk állítani ezt a partikuláris megoldást a két előbbi megoldás lineáris kombinációjaként. Legyenek:
azt kívánjuk elérni, hogy az
- αu1 + βu2 = u
- αv1 + βv2 = v
egyenletrendszernek legyen egyértelmű megoldása (α,β)-ra. Ez pontosan akkor van, ha a
determináns (azaz az egyenletrendszer x0-beli Wronsky-determinánsa) nem nulla. Hiszen ekkor a megoldás egyértelműsége miatt (azaz, hogy u és v egyértelműen meghatározza y-t) azt kapjuk, hogy (α,β) "globális konstansok is", azaz αy1 + βy2 = y.
Az egyenlet Laplace-transzformáltja:
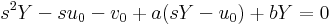
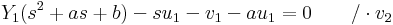
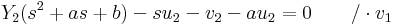
- (s2 + as + b)(v2Y1 − v1Y2) + (s + a)(u2v1 − u1v2) = 0
Ennek az egyenletnek minden s-re fenn kell állnia, ezért ha u2v1 − u1v2 = 0 lenne, akkor v2Y1 − v1Y2 = 0 is lenne (minden s-re), azaz Y2 és Y1 lineárisan kifejezhetők lennének egymással, ami ellentmondana a rájuk tett kezdeti feltevésnek.
II. A megoldéskeresési feladatot kicsit bővebb körben, a valós változós, komplex értékű kétszer folytonosan R-differenciálható függvények körében oldjuk meg. Tehát ekkor A a C2(I,C) térből a C(I,C) térbe hat. Ezek között fogunk valós megoldás keresni. A differenciáloperátornak sajátfüggvénye az exponenciális függvény, így tetszőleges λ ∈ C
próbafüggvény behelyettesítésével kapjuk:
Tehát a megoldások:
1. ha λ1 ≠ λ2 valósak, akkor
bázis, mert lineárisan függetlenek és éppen ezért I. miatt előállítják Ker(A)-t:
2. ha λ1 = λ2 valósak, akkor keresnünk kell mégegy az eλx-től lineárisan független megoldást.
Világos, hogy ez az, hiszen a 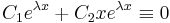 egyenletet eλx-vel leosztva, a polinom balodalú
egyenletet eλx-vel leosztva, a polinom balodalú 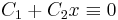 adódna, ami csak akkor lehet a nullapolinom, ha az ehók mind nullák.
adódna, ami csak akkor lehet a nullapolinom, ha az ehók mind nullák.
3. ha λ = α 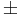 β nemvalós, akkor
β nemvalós, akkor
azaz
megoldások, melyek azonban komplexek. De ezeket összeadva, illetve a különbségüket i-vel beszorozva már valós megoldásokat kapunk (ezek az előbbi végzett műveletek lineárisak voltak, így a függvények megoldás mivoltán nem változtattak). Azaz:
a tér pedig:
bázis, mert lineárisan függetlenek és éppen ezért I. miatt előállítják Ker(A)-t.
Geometriai tenzorok
- Lásd erről még Serény jegyzetének (ps.gz/dvi) 30., 34-35., 70-72. oldalán.
A V = R2-ben, vagy R3-ban olyan matematikai objektumokat hozunk létre, melyek V minden bázisában felírva egy-egy mátrixszal jellemezhetők, de invariánsak a koordinátarendszer megváltoztatására nézve, azaz mátrixaik egymással vett szorzata (vagy összege, vagy vektorral, számmal vett szorzata) egyenlő a szorzat mátrixával. Rn-ben ilyet könnyen találunk: ezek az L(Rn,Rn)-beli lineáris operátorok:
Definíció. Az L(Rn,Rn)-beli lineáris operátorokat tenzoroknak, vagy másodrendű tenzoroknak nevezzük.
Minthogy a tenzorok maguk is invariánsak, találhatunk velük kapcsolatos további vektor, tenzor vagy skalárinvariánsokat.
Először is megfogalmazzuk, hogy mitől invariáns egy mennyiség. Legyen B és C az n dimenziós V egy-egy bázisa. Legyen T a B-t a C-re váltó koordinátaváltás transzformációja, azaz a
(tehát ez invertálható tenzor). Tudjuk hogy, ha A tetszőleges tenzor, akkor ő egy lineáris leképezés, és emiatt
Ez a tenzorok invariáns tulajdonsága.
Az f(M) ∈ R (M ∈ Mn×n) skalárfüggvényt akkor nevezzük invariánsnak, ha minden B és C bázisra és A tenzorra:
Másként, minden B bázisra, T a B megváltoztató koordinátaváltó transzformációra és A tenzorra
ahol [.] a B-beli koordinátamátrixot jelenti.
Az m(M) ∈ Mn×n (M ∈ Mn×n) mátrixfüggvényt pedig akkor nevezzük invariánsnak, ha minden B és C bázisra és A tenzorra:
azaz ha m az A mátrixával együtt transzformálódik.
Determináns
Vegyük az M  det(M) mátrixleképezést. A determinánsok szorzástétele szerint tetszőleges M és N mátrixra:
det(M) mátrixleképezést. A determinánsok szorzástétele szerint tetszőleges M és N mátrixra:
Emiatt ha A az A tenzor egy mátrixa és T a koordinátaváltó-mátrix, akkor:
Hiszen T-1T = I az egységmátrix.
Értelmes tehát az A tenzor determinánsának értelmezése úgy, hogy det(A) az A tetszőleges mátrixának determinánsa.
Nyom, trace, spur
Vegyük a következő mátrix leképezést:
azaz a mátrixok főátlóbeli elemeinek összegét. Ez is invariáns, melyet a következőkkel bizonyíthatunk. Először is belátjuk a spur szimmetrikus tulajdonságát. Tetszőleges A, B mátrixra Sp(AB) = Sp(BA). Tudjuk, hogy két mátrix szorzata a következőképpen definiált:
ezért:
Ez a képlet azt mondja, hogy "spur alatt a mátrixok kommutálnak". Az invariancia pedig:
Ez a mennyiség tehát az A tenzor egy skalárinvariánsa.
Szimmetrikus és antiszimmetrikus tenzorok
Vegyük az A lineáris leképezést és ennek az S sztenderd bázisbeli mátrixát A-t. Ekkor világos, hogy az AT transzponált mátrixszal történő AT[v]S szorzás egy lineáris leképezés, tehát tenzor, tenzortranszponálás definíciója tehát az, hogy minden A tenzorhoz hozzárendeljük a következő lineáris leképezést:
ahol  a mátrixszorzás.
a mátrixszorzás.
Ám, ez nem minden bázisban viselkedik úgy, ahogy azt a transzponálástól elvárjuk, azaz ha B egy tetszőleges bázis, akkor az [A]BT már nem feltétlejül a T-1 ATT mátrix, ahogy azt várnánk. Ellenben ortonormált bázisokra és a köztük váltó ortogonális transzformációkra már igen. Ezután a tárgyalást csak ortonormált (azaz páronként merőleges, egységhosszúságú bázisvektorú) bázisokra és az ezek között váltó OT = O-1 egyenlőségnek eleget tévő távolságtartó vagy másként ortogonális transzformációkra szorítkozunk.
Igaz az alábbi invariancia-tulajdonság. Ha B tetszőleges ortonormált bázis, [A]B=A és OT = O-1, akkor
(Felhasználtuk a szorzat transzponálásának (AB)T= BTAT szabályát -- nemdebár a mátrixszorzás nem kommutatív.) Tehát a sztenderd bázisban definiált transzponálás minden ortonormált bázisban transzponálás lesz, így ha csak ezekre szorítkozunk, akkor a AT fenti definíciója invariáns leképezést ad meg.
Lényeges tehát, hogy transzponálást, szimmetria és antiszimmetria vizsgálatokat a tenzorok tekintetében most úgy végezünk, hogy tudatában vagyunk annak, hogy eközben a hagyományos, geometriai |a||b|cos γ definíciójú skaláris szorzást használjuk (illetve ennek komponensenkénti változatát). Ezért nevezzük ezeket néha geometriai tenzoroknak.
Az S tenzor szimmetrikus, ha minden ortonormált bázisban a mátrixa szimmetrikus mátrix. Igaz az, hogy S pontosan akkor szimmetrikus, ha minden u, v vektorra
- u
 (Sv)=v
(Sv)=v (Su),
(Su),
ahol  a skaláris szorzás.
a skaláris szorzás.
Az A tenzor antiszimmetrikus, ha minden ortonormált bázisban a mátrixa antiszimmetrikus mátrix. Igaz az, hogy A pontosan akkor antiszimmetrikus, ha minden u, v vektorra
- u
 (Av)=-v
(Av)=-v (Au),
(Au),
ahol  a skaláris szorzás.
a skaláris szorzás.
Bármely T tenzor egyértélműen előáll S + A alakban, ahol S szimmetrikus, A pedig antiszimmetrikus, éspedig:
Két fontos tétel:
Tétel -- Ha A ∈R3 (illetve R2 ) antiszimmetrikus, akkor létezik olyan a vektor (vagy a skalár), hogy minden v vektorra:
a-t (ill. a-t) az A vektorinvariánsának nevezzük (bár a síkon ez skalár). A tételt elég a sztenderd bázisban igazolni, ott az a×( . ) opertátorral, azonos így A ez az operátor.
Főtengelyétel -- Ha S ∈Rn szimmetrikus, akkor minden sajátértéke valós és létezik a sajátvektorokból álló B ortonormált bázis, amiben S főtengelyre transzformálható, azaz diagonális és az elemei az S sajátértékei:
Ez nehéz, de fontos tétel.
A deriválttenzor invariánsai
Tudjuk, hogy ha v differenciálható vektorfüggvény, akkor az r0 pontbeli differenciálján, vagy deriváltján, vagy deriválttenzorán azt az egyértelműen létező A lineáris leképezést értjük, melyre:
Minthogy az A deriválttenzor maga is tenzor, ezért érdemes külön elnevezni az invariánsait (h tetszőleges vektora a térnek):
azaz A vektorinvariánsának duplája a rotáció. A divergencia a skalárinvariáns:
Világos, hogy ebből úgy lesznek a parciális deriváltakkal definiált alakok, ha a A sztenderd bázisbeli mátrixát, azaz a J Jacobi mátrixot írjuk fel. Ekkor mindkét említett differenciáloperátort a szokásos alakjában kapjuk:
Megjegyzés. A főtengelytételből következik, hogy hogyan jellemezhető az az eset, amikor az A deriváltenzor főtengelyre transzformálható. Ez pontosan akkor van, amikor rot(v)=0.
Potenciál
A továbbiakban feltesszük, hogy a v vektorfüggvény folytonosan differenciálható.
Azt mondjuk, hogy a v vektorfüggvény potenciálos, ha van olyan u skalárfüggvény, mely differenciálható és
A v vektorfüggvény cirkulációja a Γ egyszerű zárt görbén a
vonalintegrál.
A potenciálosság rendkívül szoros kapcsolatban van a cirkulációval és a rotációval:
Tétel. Ha v folyt. diff. vektormező az A egyszeresen összefüggő tartományon. Ekkor az alábbi három kijelentés egymással egyenértékű (v folyt. diff. vektormező):
- v potenciálos,
- v rotációja minden pontban nulla,
- v cirkulációja minden zárt görbére nulla (más kifejezéssel: v konzetvatív).
Bizonyítás.
1. --> 2. Tegyük fel, hogy grad u = v, így rot v = rot grad u. Ekkor formálisan hivatkozhatunk például a vektoriális szorzás azon szabályára, hogy párhuzamos vektorok vektoriális szorzata 0, hisz
De itt végül is a Young-tételről van szó. Komponensenként kiírva:
kétszer folytonsan differenciálható u Hesse-mátrixa szimmertikus, azaz a vegyes másodrendű parciális deriváltak egyenlők, azaz a fenti összeg 0.
2. --> 3. Itt a Stokes-tételre kell hivatkoznunk:
egyszeresen összefüggő tartományban haladó Γ = ∂F görbére és tetszőleges olyan F felületre, melynek ő a pereme. De rot v mindenhol 0. így a jobb oldal 0, azaz cirkuláció is.
3. --> 1. Belátjuk, hogy van potenciál. Legyen a rögzített pont és b tetszőlegesen választott. Legyen Γ1 és Γ2 két tetszőleges görbe, mely a-ból b-be megy. Ekkor az egyszeres összefüggőség miatt a Γ2 -t visszfelé irányítva:
az a zárt görbe, mely az a-ból megy a Γ1 mentén a b-be és a b-ből megy a Γ2 mentén, de ellenkezőleg irányítva az a-ba. De v minden körintegrálj eltűnik, így
azaz
Tehát az
skalárfüggvény független az úttól és a felső határ szerinti gradiense ugyanúgy az integrandus, mint az egyváltozós valós függvények esetén. QED.
Az előbb említett, az integrálfüggvény deriválhatóságának tételének megvan a párja is. Ez az első gradientétel, mely végül is nem más, mint a Newton--Leibniz-formula többdimenziós általánosításai közül a legelső verzió:
Tétel.
(ha u folyt. diff. és egysz. öf. tartományon ért.)
A tétel beleillik a "nagy integrálátalakító tételek" sorába (Stokes-tétel, Gauss--Osztrogradszkij-tétel és most az I. gradienstétel), melyek alapszlogenje, hogy "integrál a peremen = a derivált integrálja belül", persze itt a perem az {a,b} véges halmaz, a derivált a gradiens, a "belül" pedig a Γ görbe. (S.-t-nél felület a belső, a határán futó zárt görbe a perem és rot a derivált, G--O-t nél térrész a belső, az őt határoló zárt felület a perem és div a derivált).
Potenciálkeresés.
- lásd: egzakt differenciálegyenlet megoldása (un. pancsolásos módszer), komplex potenciál keresése és harmonikus társ.
- grad u = rnr típusú differenciálegyenletek megoldása
Analitikus függvény reguláris
Komplex nemnegatív kitevőjű hatványsorok
Definíció – Legyen (an) komplex számsorozat és z0 ∈ C. Ekkor a
- ∑(an(idC-z0)n)
függvénysort hatványsornak nevezzük és összegét, az
hozzárendelési utasítással értelmezett, a
- {z ∈ | ∑(an(z-z0)n) konvergál }
halmazon értelmezett függvényt a hatványsor összegének nevezzük. Középpontja z0, együtthatósorozata (an).
A továbbiakban csak a ∑(anzn) alakú, azaz a 0 körüli hatványsorokkal foglalkozunk (ezzel nem csorbítjuk az általánosságot, mert eltolással megkaphatjuk a többit is).
Tétel – Cauchy–Hadamard-tétel – Ha (an) komplex számsorozat, ![c= \limsup\limits_{n}\sqrt[n]{|a_n|}](/upload/math/0/8/a/08a549d611fba6d99576372e981e8b49.png) és
és
akkor ∑(anzn) abszolút konvergens a BR(0) gömbön és divergens a B1/R(∞) gömbön.
Bizonyítás. Nyilvánvaló, hogy a Cauchy-féle gyökkritériumot kell használni a valós értékű abszolútérték-sorozatokra. Komplex sor konvergens, ha abszolút konvergens, mert igaz, hogy minden Cauchy-sorzat konvergál C-ben.
Megjegyzés. A tételbeli R sugarat a hatványsor konvergenciasugarának nevezzük. R-et másként is kiszámíthajuk. Ha azt tudjuk, a hányadoskritérium alapján, hogy
akkor létezik és ezzel egyenlő az n-edik gyökök sorozata is:
ahol az idézőjel azt jelzi, hogy a konvergenciasugár lehet végtelen vagy 0 is.
Példa. Az alábbi mértani sor konvergens, ha |z|<1 és összege a szokásos:
Példa.Minden z ∈ C-re konvergens az
sor, mert konvergenciasugara ∞. Ezt legegyszerűbben a hányadoskritéruimmal és a fenti megjegyzéssel állapíthatjuk meg:
A tétel
Reguláris egy függvény, ha egy nyílt halmazon komplex differenciálható. A hatványsorok ilyenek.
Tétel – Ha (an) komplex számsorozat, akkor az ∑(anzn) hatványsor összegfüggvénye komplex differenciálható a konvergenciakör belsejében.
Másként fogalmazva:
Analitikus függvény reguláris. Hiszen, ha f analitikus, akkor lokálisan hatványsor.
Bizonyítás. Belátjuk, hogy a hatványsor a középpont körüli elég kis körben mindenütt differenciálható. Legyen R a konvergenciasugár, egyelőre legyen r < R (később erre adunk becslést) és legyen
továbbá Δz olyan, hogy
még mindig teljesüljön.
A következő függvény z-beli komplex differenciálhatóságát kell belátni:
Nem árulunk zsákbamacskát, formális tagonkénti deriválással megkapható az a sor, mely ennek a függvénynek a majdani deriváltja lesz:
Világos, hogy ez utóbbi sor is konvergens a konvergenciakör belsejében. Erről a Cauchy--Hadamard-tétellel győződhetünk meg, ha |z|< R, így:
Képezzük a különbségi hányadost és vonjuk le belőle ezt a kifejezést!
ekkor a kéttagú összeg négyzetére vonatkozó
algebrai azonossággal alakítjuk át a hatványt, majd amivel lehet leosztunk és amit lehet kiemelünk:
Azt kell ellenőrizni, hogy második tényezőben lévő sor konvergens-e, hiszen ekkor a véges összeget a nullához tartóval összeszorozva nullához tartót kapunk. Ezt a gyökkritériummal látjuk be:
itt |z|-t korlátoztuk 1-nél kisebbre, |Δz|-t pedig nemnulla, de |z|-nél kisebbre (z=0 triviális eset). A konvergencia ekkor
amennyiben az |Δz| < |z| < r olyan, hogy r < 1/(2R).
Így a különbségi hányados minusz a majdani derivált abszolút eltérése felülbecsülhető egy nullához tartó szor korlátos függvénnyel, azaz P deriválató z-ben és a deriváltja a formális tagonkénti deriválással kapott sor. A korlátosság onnan adódik, hogy hatványsor összegfüggvénye folytonos és a min{1/(2R),R/2} sugarú zárt körön, mint kompakt halmazon korlátos.
Komplex körintegrálok
Ebben a tételben a komplex körintegrálok kiszámításával foglalkozunk.
Az f folytonos komplex függvény komplex integrálját egy szakaszonként folytonosan differenciálható G: [a,b]  C görbe mengtén értelmezhetjük közvetlenül a C síkon a
C görbe mengtén értelmezhetjük közvetlenül a C síkon a
Riemann-közelítőösszeg határátmenetével vagy a síkbeli vonalintegrálra visszavezetve. Ez utóbbi esetben válik kifehezetten szembetűnővé, hogy a fenti képletben a  szorzás a komplex szorzás. Ha ugyanis f= u + iv, akkor az f=(u,v) vektormezőnek olyan differenciálforma szerinti integrálja a komplex pályamenti integrál, mely az f=(u,v) vektor és a dz=(dx,dy) infinitezimális elmozdulásvektor komplex szorzásaként jön létre:
szorzás a komplex szorzás. Ha ugyanis f= u + iv, akkor az f=(u,v) vektormezőnek olyan differenciálforma szerinti integrálja a komplex pályamenti integrál, mely az f=(u,v) vektor és a dz=(dx,dy) infinitezimális elmozdulásvektor komplex szorzásaként jön létre:
Ebben a felírásban az (u,-v) és (v,u) olyan segédvektormezők, melyek vonalintegráljai adják meg a komplex integrál valós és képzetes részét. Tehát az integrált a
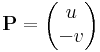 és
és 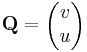
segédvektormezők síkbeli vonalintegráljai, vagy a
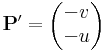 és
és 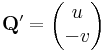
segédvektormezők síkbeli felületi integráljai szolgáltatják.
Itt érdemes feleleveníteni, hogy az S = (s1, s2) síkvektormező felületi integrálja nem más, mint a ( − s2, s1) vektormező vonalintegrálja (a megfelelő irányítással).
megfelelő módon irányítva az F felületet, ill ennek "F" görbe mivoltát.
(Azaz a s_2dx - s_1 dy differenciálforma integrálja. Differenciálforma -- nemes egyszerűséggel -- egy olyan kifejezése, ahol dx, dy, dz-k és egy vektormező komponensei vannak összeszorozva-összeadva.)
Primitívfüggvény
A G: [a,b]  C görbe zárt görbe, ha G(a)=G(b). A zárt görbére vett integrál a körintegrál.
C görbe zárt görbe, ha G(a)=G(b). A zárt görbére vett integrál a körintegrál.
Az első eszköz a Newton--Leibniz-formulából következik, hisz ha F'=f, akkor ∫zw f = F(w) - F(z).
Tétel. Ha a D tartományon értelmezett f függvénynek van primitív függvénye, akkor a körintegrál minden a D-ben haladó zárt görbén eltűnik:
Példa. Az 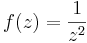 -nek van primitívfüggvény, így körintegrálja mindenütt eltűnik.
-nek van primitívfüggvény, így körintegrálja mindenütt eltűnik.
Példa. Paraméteresen kiszámolható, hogy
akrámilyen r > 0 sugárra. Tehát a teljes C \ {0}-n a reciproknak nincs primitívfüggvénye. (De egyszeresen összefüggő, a 0-t nem tartalmazó tartományon már van: a logaritmus.)
A komplex analízis főtétele
A komplex N--L-tétel nem túl hatékony eszköz. A N--L-tétel síkvektoranalízisbeli általánosításához kell folyamodnunk, például a Gauss-tételhez, ha többet akarunk mondani:
Gauss-tétel (R2-re) Legyen D egyszeresen összefüggő, síktartomány és legyen G : r=r(t) ennek határát paraméterező zárt görbe. Ha v folytonosan R-differenciálható a D lezártján, akkor
A tételben rendkívül lényeges az egyszeres összefüggőség kitétel (ahogy a folytonos differenciálhatóság is). Gondoljunk csak a térbeli v(r) = r/|r|3 vektormezőre. Ennek körintegrálja az origóközéppontú gömbön 4π, miközben a divergenciája mindenhol 0.
Így tehát a komplex vonalintegrál kiszámításához csak a P ' és Q ' felületi integrálját kell kiszámítanunk, amihez a Gauss-tétel miatt a divergenciákat ki kell kiszámítanunk:
Ami, a C-R-egyenletek miatt igaz.
Innen
Goursat ennél is mélyebb eredményt talált:
Goursat-lemma. A T háromszöglapon reguláris f komplex függvény integrálja a háromszög határán nulla:
Innen már könnyen adódik a komplex analízis főtétele, melyet először Cauchy modott ki ugyan csak folytonosan diffható komplex függvényre, de Goursat ezt megfejelte a gyengített feltételével:
Cauchy-tétel vagy Főtétel. Ha a D tartományon egyszeresen összefüggő tartományon reguláris az f komplex függvény, akkor a tartományban minden zárt G görbén a függvény integrálja nulla:
Cauchy-formula
A Cauchy-formula azért múlhatatlan fontosságú, mert ennek a kifejezetten komplex jellegű állításnak a következménye, hogy egy reguláris függvény nem csak egyszer, de végtelenszer differenciálható, sőt analitikus.
Tétel. Ha f az z_0 egy U környezetén reguláris, akkor tetszőleges az U-ban haladó, a z_0-t egyszer körülhurkoló pozitívan irányított G zárt görbére:
Bizonyítás. Vegyünk a z0 körül egy olyan K kört, mely a pozitívan irányított G belsejében halad és r > 0 sugarú. Definiáljuk azt a görbét melyet a következőkppen kapunk. Metszük át egy befelé menő s sugárral a G és K közötti tartományt. Tegyük fel, hogy G és K kezdőpontjai a sugár metszetei. tákoljuk össze a következő görbét:
Világos, hogy ekkor a Γ-ra vett körintegrál eltűnik, másrész szakaszonként intergálva a Γ-n:
mivel az s-en oda-vissza integrálva az integrálösszeg nulla és a Γ-ban a negatívan irányított K-t kell venni. Emiatt:
Vagy hivatkozva egy a gyakorlaton vett lemmára: egyetlen izolált szinguláris hely körüli görbén az integrál ugyanaz, mint az integrál a pont körüli kis körön.
Márcsak ennek az f(z0)-lal arányos voltát kell belátni:
ebből a tagok:
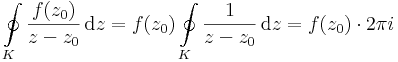
- minthogy a reciprok körintegrálja 2πi (egy egyszerű zárt görbén).
másrészt az f függvény z0-beli folytonossága miatt tetszőleges ε > 0 számhoz létezik olyan z0 körüli környezet, hogy ha K abban van, azaz a sugara, az r elég kicsi, akkor |f(z)-f(z0)| < ε; emiatt
Vagyis az utolsó tag nulla így a formulát megkaptuk.
Riemann-tétel
Tétel. Legyen U nyilt tartomány, z0 ∈ U. Ha f az U\{z0}-on reguláris és korlátos, akkor minden U-beli körintegrálja eltűnik.
Bizonyítás. Belátjuk, az f Laurent-sora csak reguláris részből áll a z0 körül. Az Laurent-sor együtthatóformuláiból, k < 0 egészre és Kr r sugarú körre:
hiszen f korlátjához létezik olyan kis környzet, ahol a nullához tartó második tényező K-nál kisebb (vagy 1, és akkor a képletben és a végeredméybencsak K szerepel). Ha pedig r-rel tartunk a 0-hoz, az együttható eltűnik.
f-tehát kiterjeszthető U-n reguláris függvénnyé, így a Cauchy-tétel miatt minden körintegrálja eltűnik. Vagy egyszerűbben: f reziduuma a megszüntethető szingularitási helyen 0.
Reguláris függvény analitikus, Laurent-sorfejtés
Tétel. -- A Laurent-sor tétele -- Ha az f: C  C és a ∈ C szám és 0 ≤ r < R ≤ +∞ olyan sugarak, hogy f az
C és a ∈ C szám és 0 ≤ r < R ≤ +∞ olyan sugarak, hogy f az
nyílt körgyűrűben reguláris, akkor egyértelműen léteznek olyan (cn)n∈Z komplex számok, éspedig tetszőleges a T-ben haladó az a-t egyszer pozitív irányban körbehurkoló G görbére:
hogy a
függvénysor konvergens T-ben és minden z ∈ T számra:
Bizonyítás. f-et most nem tudjuk előállítani a Cauchy-integrálformulával, mint a Taylor-sor esetén, mert az a pontban esetleg a függvény nem reguláris. De előállíthatjuk két hasonló formula különbségeként.
Rögzítsük egy tetszőlegesen választott z ∈ T-t. Legyenek k1 és k2 két a középpontú, T-ben haladó, pozitívan irányított kör, úgy, hogy z a k1 és k2 körök közötti nyílt tartományba essen. Ezekből a körökből és az őket elválasztó gyűrűt sugárirányban befelé átmetsző s szakaszból elkészítünk egy olyan zárt görbét, melyre már alkalmazható az integrálformula. Tekintsük úgy, hogy k1 kezdő és végpontja az s kezdőpontja, k2 kezdő és végpontja pedig az s végpontja. Legyen
itt (-s) az s-sel ellenkező irányítású szakaszt jelzi. Ekkor Γ a z-t egy reguláris tartományban hurkolja egyszer, pozitívan körbe, így a Cauchy-integrálformulával:
Node, ebben az integálban az s íven kétszer oda-vissza végezzük el az integrálást, így az erre vett integrál eltűnik. Másrészt a (-k2)-n vett integrál ellenkezője a 'k2-vettének, így végülis:
Hangsúlyozzuk, hogy z és a most konstansok, így a
az értelmezési tartományán analitikus függvény. Ennek -- szikásos módon a mértani sor összegére vonatkozó képlet segítségével -- elvégezhetjük az a középpontú, valamilyen körön belüli hatványsorba fejtését. Természetesen a |w-a| < |z-a| feltételt meg kell követelnünk, hiszen hatványsor konvergenciakörében nem lehet benne a z szakadási pont. Tegyük fel tehát, hogy |w-a| < |z-a|. Ekkor:
Ezzel megvan a sorfejtés minden együtthatója, ugyanis 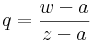 -ra kell alkalmazni a mértani sor formuláját:
-ra kell alkalmazni a mértani sor formuláját:
1) Világos, hogy ezt a sorfejtést csak a k2-re vonatkozó integrálban használhatjuk fel, mert ott lesz a q < 1 (ill. a w mindig közelebb a-hoz mint z-hez). Ezt az integrált tehát:
az integrál felcserélhető a szummával és a w-től független tagok kihozhatók az integrál elé, ezért
Ekkor egy konvergens, negatív kitevőjű hatványsort kaptunk, melynek csak főrésze van, de érdekes módon nem a középponttal és w-re, hanem a középponttal és z-ra. Ez pont a kívánt sorfejtés, melyet érdemes átindexelni úgy, hogy a szummázás -1-től induljon és -∞-ig menjen:
Már csak azt kell megmagyaráznunk, hogy a k2 helyére most már minden olyan G görbére felírható, mely az a-t pozitívan öleli körbe egyszer és a regularitási tartományban halad. Valóban, a képletbeli integrál már független az 1/(w-z) sorfejtési szituációjától és minden olyan G görbére áttranszformálható melyek folytonosan áttranszformálható k2-be. Ez a T körgyűrű összes a tételi állításban megadott görbéjére áll.
2) Most már az előző számolásból sejthető, hogy a Laurent-sor reguláris része akkor jön ki, ha az 1/(w-z) reciprokfüggvényt a az a körül nem pozitív, hanem negatív kitevőjű hatványsorba, fejtjük -- mint az első példában. Ezt a |w-a| > |z-a| feltétellel tehetjük csak meg, hisz ilyen sor konvergenciatartománya körgyűrű és a z szinguláris pontot nem tartalmazhatja:
Ez a sor valóban akkor konvergens, ha |w-a| > |z-a|. Ezzel az előző pomt számolását elvégezve az f(z)-t előállító Laurent-sor reguláris részét kapjuk. QED
Következmény. Reguláris függvény analitikus.
Következmény. Az izolált szingularitások a sorfejtés szerint osztályozhatóak éspedig. Az f függvény z0 izolált szinguláris pontja körüli sorfejtésben
- pontosan akkor van csak reguláris tag, ha a szingularitás megszüntethető,
- pontosan akkor van véges sok főrészbeli tag, ha végtelen a határérék z0-ban,
- pontosan akkor van végtelen sok főrészbeli tag (lényeges szingularitás), ha nem létezik a határérék z0-ban.
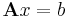
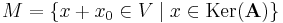
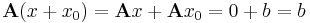
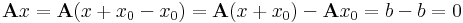
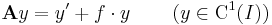
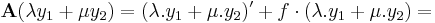



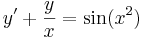
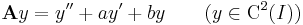
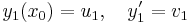
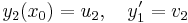
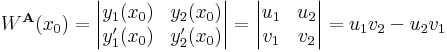
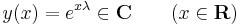
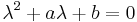
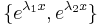
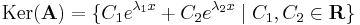
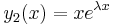
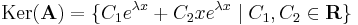



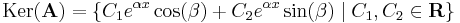

![[\mathbf{A}]_C=[\mathbf{T}^{-1}]_B[\mathbf{A}]_B[\mathbf{T}]_B\,](/upload/math/1/e/8/1e86f5ac6238920be02735a4995475fc.png)
![f([\mathbf{A}]_C)=f([\mathbf{A}]_B)\,](/upload/math/4/1/3/413f64190dcf29a18a75473d47f8e612.png)
![f([\mathbf{A}])=f([\mathbf{T}^{-1}][\mathbf{A}][\mathbf{T}])\,](/upload/math/5/b/6/5b60873191e7c52251cbcbd7f4a2b39e.png)
![m([\mathbf{A}]_C)=[\mathbf{T}^{-1}]m([\mathbf{A}]_B)[\mathbf{T}])\,](/upload/math/3/a/3/3a3bd86297790dd047e40a881ce829b3.png)
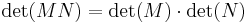
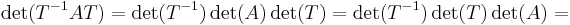
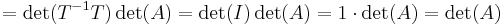
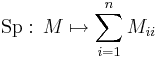
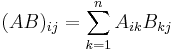
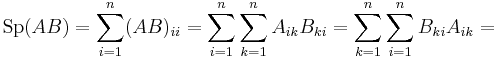
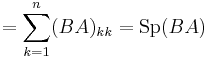
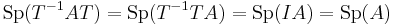
![\mathbf{A}^{\mathrm{T}}\mathbf{v}=[\mathbf{A}]_S^T\cdot [\mathbf{v}]_S\,](/upload/math/0/a/3/0a3e3168846ab0faa0d695ff3dc4f954.png)
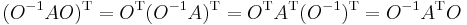
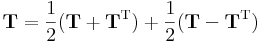
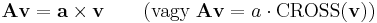
![[\mathbf{S}]_{\{\mathbf{v}_1,...,\mathbf{v}_n\}}=\begin{pmatrix}\lambda_1& 0& 0\\
0& \ddots& 0\\
0 & 0& \lambda_n\end{pmatrix}](/upload/math/2/b/6/2b6d68afeb211967e07984838ae5f4a1.png)
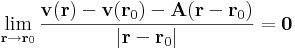
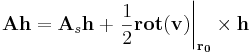

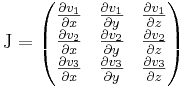
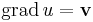
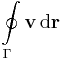
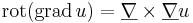
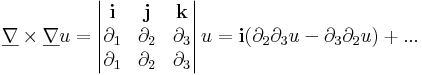
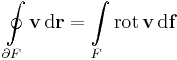
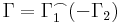
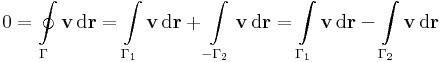
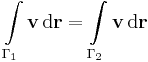
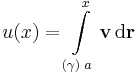
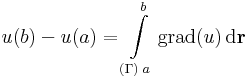
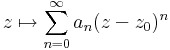
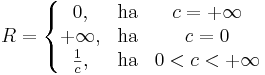
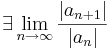
![\exists\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}=\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|}=\,''\,\frac{1}{R}\,''](/upload/math/2/1/0/210b8f12a11f0846e6103b096dee2a3d.png)



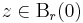
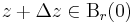

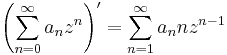
![\limsup\limits_{n\to \infty}\sqrt[n]{|a_{n}|\cdot n }=\limsup\limits_{n\to \infty}\sqrt[n]{|a_{n}|}\cdot 1=\frac{1}{R}\,](/upload/math/5/7/c/57ca0d31da52e342a251e1cc555470e9.png)
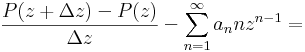


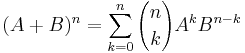
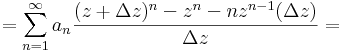
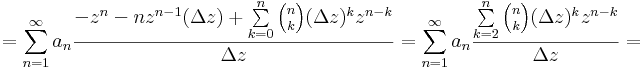



![\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|\cdot 2^n\cdot |\Delta z |^{n-2}\}}=\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|}\cdot 2 \cdot |\Delta z|<\frac{1}{R}R=1\,](/upload/math/1/5/f/15f72212ba98e9ee4cab8226fe265e98.png)