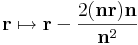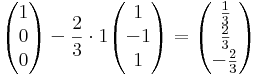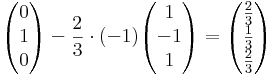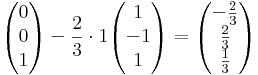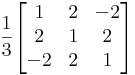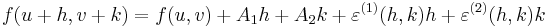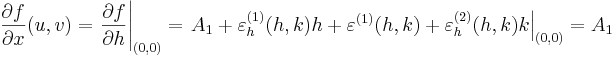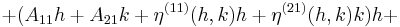Szerkesztő:Mozo/egyéb

A MathWikiből
< Szerkesztő:Mozo(Változatok közti eltérés)
(→Tükrözés síkra)
(→Young-tétel)
 
(egy szerkesztő 8 közbeeső változata nincs mutatva)
15. sor: 15. sor:
 
\end{bmatrix}</math>
 
\end{bmatrix}</math>
 
ez -1 determinánsú szimmetrikus mátrix, ortonormált vektorokból álló sajátrendszerrel,
 
ez -1 determinánsú szimmetrikus mátrix, ortonormált vektorokból álló sajátrendszerrel,
 +
 +
==Young-tétel==
 +
'''Tétel''' (''Gyenge Young-tétel'') ''U'' = B<sub>&delta;</sub>(''a'') &sube; '''R'''<sup>2</sup>, ''f'': ''U'' <math>\to</math> '''R''',
 +
:''f'' &isin; C<sup>&infin;</sup>(''U'') és ''f''<sup>(n)</sup> egyenletesen korlátos
 +
akkor
 +
:&part;<sub>21</sub>f = &part;<sub>12</sub>f
 +
 +
 +
''Bizonyítás.'' a=(u,v), (x,y)=(u+h,v+k) &isin; B<sub>&delta;</sub>(a), A<sub>1</sub> = &part;<sub>1</sub>f(a), A<sub>2</sub> = &part;<sub>2</sub>f(a), A<sub>ij</sub> = &part;<sub>ij</sub>f(a).
 +
 +
:<math>f(u+h,v+k)=f(u,v) + A_1h + A_2k + \,</math>
 +
:<math>+ A_{11}h^2 + A_{12}hk + A_{21}kh + A_{22}k^2 + r_3(h,k)\,</math>
 +
ahol
 +
:<math>r_3(h,k)=\sum\limits_{i=0}^{3}\varepsilon_{i}(h,k)\cdot h^ik^{3-i}\,</math>
 +
harmadrendűen kicsiny, de differenciálható tagok. Ekkor
 +
:<math>\partial_1f(x,y)=\frac{\partial f(h,k)}{\partial h}=A_1+2A_{11}h+A_{12}k+A_{21}k+\frac{\partial r_3(h,k)}{\partial h}\,</math>
 +
:<math>\partial_{21}f(x,y)=\frac{\partial^2 f(h,k)}{\partial k\partial h}=A_{12}+A_{21}+\frac{\partial^2 r_3(h,k)}{\partial k\partial h}\,</math>
 +
ez a (h,k)=(0,0)-ban:
 +
:<math>\partial_{21}f(u,v)=A_{12}+A_{21}\,</math>
 +
mert a harmadrendűen kicsiny tagok a (h,k)=(0,0)-ban eltűnnek. Ugyanígy:
 +
:<math>\partial_{12}f(u,v)=A_{12}+A_{21}\,</math>
 +
így ezek is egyenlők.
 +
 +
'''Gondolatkísérlet'''
 +
:<math>f(u+h,v+k)=f(u,v) + A_1h + A_2k + \varepsilon^{(1)}(h,k)h+\varepsilon^{(2)}(h,k)k</math>
 +
 +
ha az &epsilon;-ok diff.-hatóak, akkor:
 +
 +
:<math>\frac{\partial f}{\partial x}(u,v)=\left.\frac{\partial f}{\partial h}\right|_{(0,0)}=\left.A_1 + \varepsilon^{(1)}_h(h,k)h+\varepsilon^{(1)} (h,k)+\varepsilon^{(2)}_h(h,k)k\right|_{(0,0)}=A_1</math>
 +
ugyanígy
 +
:<math>\frac{\partial f}{\partial y}(u,v)=\left.\frac{\partial f}{\partial h}\right|_{(0,0)}=A_2</math>
 +
 +
De ennél többet is mondhatunk. Ha az &epsilon;-okon kívül a parciális differenciálok és az epszilon másoderndű tagjának függvényegyütthatója is differenciálható, akkor:
 +
 +
:<math>f(u+h,v+k)=f(u,v) + A_1h + A_2k +\,</math>
 +
:<math>+(A_{11}h + A_{21}k + \eta^{(11)}(h,k)h+\eta^{(21)}(h,k)k)h+ \,</math>
 +
:<math>+(A_{21}h + A_{22}k + \eta^{(21)}(h,k)h+\eta^{(22)}(h,k)k)k= \,</math>
 +
:<math>=f(u,v) + A_1h + A_2k +\,</math>
 +
:<math>+A_{11}h^2 + A_{21}kh + \eta^{(11)}(h,k)h^2+\eta^{(21)}(h,k)kh+ \,</math>
 +
:<math>+A_{21}hk + A_{22}k^2 + \eta^{(21)}(h,k)hk+\eta^{(22)}(h,k)k^2= \,</math>
 +
ha most mindegyik &eta; deriválható, akkor:
 +
:<math>\frac{\partial f(u+h,v+k)}{\partial h}=A_1 + 2A_{11}h + A_{21}k + \frac{\partial \eta^{(11)}(h,k)}{\partial h}h^2+ \eta^{(11)}(h,k)2h+\frac{\partial\eta^{(21)}(h,k)}{\partial h}k+\eta^{(21)}(h,k)k+ \,</math>
 +
:<math>+A_{21}hk + A_{22}k^2 + \eta^{(21)}(h,k)hk+\eta^{(22)}(h,k)k^2= \,</math>

A lap jelenlegi, 2008. március 28., 18:19-kori változata

Tükrözés síkra

Példa. Tekintsük az S = {(x,y,z) ∈ R3 | x-y+z=0 } síkot. Adjuk meg az S síkra történő tükrözés mátrixát, a sajátvektorait és a sajátaltereket, illetve a sajátkoordinátarendszert!

A síkra tükrözés hozzárendelési utasítása:

\mathbf{r}\mapsto \mathbf{r}-\frac{2(\mathbf{n}\mathbf{r})\mathbf{n}}{\mathbf{n}^2}

ahol n a sík normálvektora, itt (1,-1,1). A bázisok képei:

\begin{pmatrix}1\\0\\0\end{pmatrix} - \frac{2}{3}\cdot 1\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}\frac{1}{3}\\\frac{2}{3}\\-\frac{2}{3}\end{pmatrix}
\begin{pmatrix}0\\1\\0\end{pmatrix} - \frac{2}{3}\cdot (-1)\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}\frac{2}{3}\\\frac{1}{3}\\\frac{2}{3}\end{pmatrix}
\begin{pmatrix}0\\0\\1\end{pmatrix} - \frac{2}{3}\cdot 1\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}-\frac{2}{3}\\\frac{2}{3}\\\frac{1}{3}\end{pmatrix}

A mátrix:

\frac{1}{3}\begin{bmatrix} 1 & 2 & -2\\ 2 & 1 & 2\\ -2 & 2 & 1 \end{bmatrix}

ez -1 determinánsú szimmetrikus mátrix, ortonormált vektorokból álló sajátrendszerrel,

Young-tétel

Tétel (Gyenge Young-tétel) U = Bδ(a) ⊆ R2, f: U \to R,

f ∈ C∞(U) és f(n) egyenletesen korlátos

akkor

∂21f = ∂12f


Bizonyítás. a=(u,v), (x,y)=(u+h,v+k) ∈ Bδ(a), A1 = ∂1f(a), A2 = ∂2f(a), Aij = ∂ijf(a).

f(u+h,v+k)=f(u,v) + A_1h + A_2k + \,
+ A_{11}h^2 + A_{12}hk + A_{21}kh + A_{22}k^2 + r_3(h,k)\,

ahol

r_3(h,k)=\sum\limits_{i=0}^{3}\varepsilon_{i}(h,k)\cdot h^ik^{3-i}\,

harmadrendűen kicsiny, de differenciálható tagok. Ekkor

\partial_1f(x,y)=\frac{\partial f(h,k)}{\partial h}=A_1+2A_{11}h+A_{12}k+A_{21}k+\frac{\partial r_3(h,k)}{\partial h}\,
\partial_{21}f(x,y)=\frac{\partial^2 f(h,k)}{\partial k\partial h}=A_{12}+A_{21}+\frac{\partial^2 r_3(h,k)}{\partial k\partial h}\,

ez a (h,k)=(0,0)-ban:

\partial_{21}f(u,v)=A_{12}+A_{21}\,

mert a harmadrendűen kicsiny tagok a (h,k)=(0,0)-ban eltűnnek. Ugyanígy:

\partial_{12}f(u,v)=A_{12}+A_{21}\,

így ezek is egyenlők.

Gondolatkísérlet

f(u+h,v+k)=f(u,v) + A_1h + A_2k + \varepsilon^{(1)}(h,k)h+\varepsilon^{(2)}(h,k)k

ha az ε-ok diff.-hatóak, akkor:

\frac{\partial f}{\partial x}(u,v)=\left.\frac{\partial f}{\partial h}\right|_{(0,0)}=\left.A_1 + \varepsilon^{(1)}_h(h,k)h+\varepsilon^{(1)} (h,k)+\varepsilon^{(2)}_h(h,k)k\right|_{(0,0)}=A_1

ugyanígy

\frac{\partial f}{\partial y}(u,v)=\left.\frac{\partial f}{\partial h}\right|_{(0,0)}=A_2

De ennél többet is mondhatunk. Ha az ε-okon kívül a parciális differenciálok és az epszilon másoderndű tagjának függvényegyütthatója is differenciálható, akkor:

f(u+h,v+k)=f(u,v) + A_1h + A_2k +\,
+(A_{11}h + A_{21}k + \eta^{(11)}(h,k)h+\eta^{(21)}(h,k)k)h+ \,
+(A_{21}h + A_{22}k + \eta^{(21)}(h,k)h+\eta^{(22)}(h,k)k)k= \,
=f(u,v) + A_1h + A_2k +\,
+A_{11}h^2 + A_{21}kh + \eta^{(11)}(h,k)h^2+\eta^{(21)}(h,k)kh+ \,
+A_{21}hk + A_{22}k^2 + \eta^{(21)}(h,k)hk+\eta^{(22)}(h,k)k^2= \,

ha most mindegyik η deriválható, akkor:

\frac{\partial f(u+h,v+k)}{\partial h}=A_1 + 2A_{11}h + A_{21}k + \frac{\partial \eta^{(11)}(h,k)}{\partial h}h^2+ \eta^{(11)}(h,k)2h+\frac{\partial\eta^{(21)}(h,k)}{\partial h}k+\eta^{(21)}(h,k)k+ \,
+A_{21}hk + A_{22}k^2 + \eta^{(21)}(h,k)hk+\eta^{(22)}(h,k)k^2= \,
A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Szerkeszt%C5%91:Mozo/egy%C3%A9b&oldid=3483”
Személyes eszközök