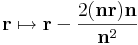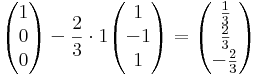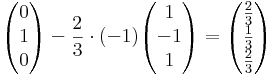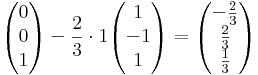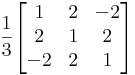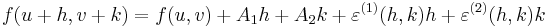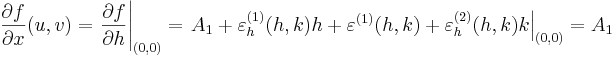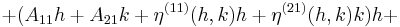Szerkesztő:Mozo/egyéb

Tükrözés síkra

Példa. Tekintsük az S = {(x,y,z) ∈ R³ | x-y+z=0 } síkot. Adjuk meg az S síkra történő tükrözés mátrixát, a sajátvektorait és a sajátaltereket, illetve a sajátkoordinátarendszert!

A síkra tükrözés hozzárendelési utasítása:

$\mathbf{r}\mapsto \mathbf{r}-\frac{2(\mathbf{n}\mathbf{r})\mathbf{n}}{\mathbf{n}^2}$

ahol n a sík normálvektora, itt (1,-1,1). A bázisok képei:

$\begin{pmatrix}1\\0\\0\end{pmatrix} - \frac{2}{3}\cdot 1\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}\frac{1}{3}\\\frac{2}{3}\\-\frac{2}{3}\end{pmatrix}$

$\begin{pmatrix}0\\1\\0\end{pmatrix} - \frac{2}{3}\cdot (-1)\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}\frac{2}{3}\\\frac{1}{3}\\\frac{2}{3}\end{pmatrix}$

$\begin{pmatrix}0\\0\\1\end{pmatrix} - \frac{2}{3}\cdot 1\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}-\frac{2}{3}\\\frac{2}{3}\\\frac{1}{3}\end{pmatrix}$

A mátrix:

$\frac{1}{3}\begin{bmatrix} 1 & 2 & -2\\ 2 & 1 & 2\\ -2 & 2 & 1 \end{bmatrix}$

ez -1 determinánsú szimmetrikus mátrix, ortonormált vektorokból álló sajátrendszerrel,

Young-tétel

Tétel (Gyenge Young-tétel) U = B_δ(a) ⊆ R², f: U $\to$ R,

f ∈ C^∞(U) és f⁽ⁿ⁾ egyenletesen korlátos

akkor

∂₂₁f = ∂₁₂f

Bizonyítás. a=(u,v), (x,y)=(u+h,v+k) ∈ B_δ(a), A₁ = ∂₁f(a), A₂ = ∂₂f(a), A_ij = ∂_ijf(a).

$f(u+h,v+k)=f(u,v) + A_1h + A_2k + \,$

$+ A_{11}h^2 + A_{12}hk + A_{21}kh + A_{22}k^2 + r_3(h,k)\,$

ahol

$r_3(h,k)=\sum\limits_{i=0}^{3}\varepsilon_{i}(h,k)\cdot h^ik^{3-i}\,$

harmadrendűen kicsiny, de differenciálható tagok. Ekkor

$\partial_1f(x,y)=\frac{\partial f(h,k)}{\partial h}=A_1+2A_{11}h+A_{12}k+A_{21}k+\frac{\partial r_3(h,k)}{\partial h}\,$

$\partial_{21}f(x,y)=\frac{\partial^2 f(h,k)}{\partial k\partial h}=A_{12}+A_{21}+\frac{\partial^2 r_3(h,k)}{\partial k\partial h}\,$

ez a (h,k)=(0,0)-ban:

$\partial_{21}f(u,v)=A_{12}+A_{21}\,$

mert a harmadrendűen kicsiny tagok a (h,k)=(0,0)-ban eltűnnek. Ugyanígy:

$\partial_{12}f(u,v)=A_{12}+A_{21}\,$

így ezek is egyenlők.

Gondolatkísérlet

$f(u+h,v+k)=f(u,v) + A_1h + A_2k + \varepsilon^{(1)}(h,k)h+\varepsilon^{(2)}(h,k)k$

ha az ε-ok diff.-hatóak, akkor:

$\frac{\partial f}{\partial x}(u,v)=\left.\frac{\partial f}{\partial h}\right|_{(0,0)}=\left.A_1 + \varepsilon^{(1)}_h(h,k)h+\varepsilon^{(1)} (h,k)+\varepsilon^{(2)}_h(h,k)k\right|_{(0,0)}=A_1$

ugyanígy

$\frac{\partial f}{\partial y}(u,v)=\left.\frac{\partial f}{\partial h}\right|_{(0,0)}=A_2$

De ennél többet is mondhatunk. Ha az ε-okon kívül a parciális differenciálok és az epszilon másoderndű tagjának függvényegyütthatója is differenciálható, akkor:

$f(u+h,v+k)=f(u,v) + A_1h + A_2k +\,$

$+(A_{11}h + A_{21}k + \eta^{(11)}(h,k)h+\eta^{(21)}(h,k)k)h+ \,$

$+(A_{21}h + A_{22}k + \eta^{(21)}(h,k)h+\eta^{(22)}(h,k)k)k= \,$

$=f(u,v) + A_1h + A_2k +\,$

$+A_{11}h^2 + A_{21}kh + \eta^{(11)}(h,k)h^2+\eta^{(21)}(h,k)kh+ \,$

$+A_{21}hk + A_{22}k^2 + \eta^{(21)}(h,k)hk+\eta^{(22)}(h,k)k^2= \,$

ha most mindegyik η deriválható, akkor:

$\frac{\partial f(u+h,v+k)}{\partial h}=A_1 + 2A_{11}h + A_{21}k + \frac{\partial \eta^{(11)}(h,k)}{\partial h}h^2+ \eta^{(11)}(h,k)2h+\frac{\partial\eta^{(21)}(h,k)}{\partial h}k+\eta^{(21)}(h,k)k+ \,$

$+A_{21}hk + A_{22}k^2 + \eta^{(21)}(h,k)hk+\eta^{(22)}(h,k)k^2= \,$