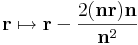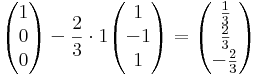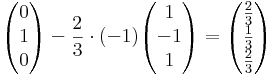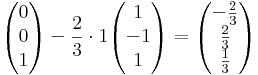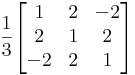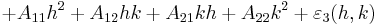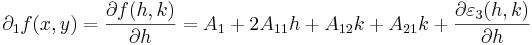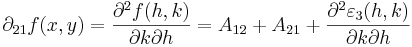Szerkesztő:Mozo/egyéb

Tükrözés síkra

Példa. Tekintsük az S = {(x,y,z) ∈ R³ | x-y+z=0 } síkot. Adjuk meg az S síkra történő tükrözés mátrixát, a sajátvektorait és a sajátaltereket, illetve a sajátkoordinátarendszert!

A síkra tükrözés hozzárendelési utasítása:

$\mathbf{r}\mapsto \mathbf{r}-\frac{2(\mathbf{n}\mathbf{r})\mathbf{n}}{\mathbf{n}^2}$

ahol n a sík normálvektora, itt (1,-1,1). A bázisok képei:

$\begin{pmatrix}1\\0\\0\end{pmatrix} - \frac{2}{3}\cdot 1\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}\frac{1}{3}\\\frac{2}{3}\\-\frac{2}{3}\end{pmatrix}$

$\begin{pmatrix}0\\1\\0\end{pmatrix} - \frac{2}{3}\cdot (-1)\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}\frac{2}{3}\\\frac{1}{3}\\\frac{2}{3}\end{pmatrix}$

$\begin{pmatrix}0\\0\\1\end{pmatrix} - \frac{2}{3}\cdot 1\begin{pmatrix}1\\-1\\1\end{pmatrix}=\begin{pmatrix}-\frac{2}{3}\\\frac{2}{3}\\\frac{1}{3}\end{pmatrix}$

A mátrix:

$\frac{1}{3}\begin{bmatrix} 1 & 2 & -2\\ 2 & 1 & 2\\ -2 & 2 & 1 \end{bmatrix}$

ez -1 determinánsú szimmetrikus mátrix, ortonormált vektorokból álló sajátrendszerrel,

Young-tétel

Tétel (Young) U = B_δ(a) ⊆ R², f: U $\to$ R,

f ∈ C^ω(U),

akkor

∂₂₁f = ∂₁₂f

Bizonyítás. a=(u,v), (x,y)=(u+h,v+k) ∈ B_δ(a), A₁ = ∂₁f(a), A₂ = ∂₂f(a), A_ij = ∂_ijf(a).

$f(u+h,v+k)=f(u,v) + A_1h + A_2k + \,$

$+ A_{11}h^2 + A_{12}hk + A_{21}kh + A_{22}k^2 + \varepsilon_3(h,k)\,$

$\partial_1f(x,y)=\frac{\partial f(h,k)}{\partial h}=A_1+2A_{11}h+A_{12}k+A_{21}k+\frac{\partial\varepsilon_3(h,k)}{\partial h}\,$

$\partial_{21}f(x,y)=\frac{\partial^2 f(h,k)}{\partial k\partial h}=A_{12}+A_{21}+\frac{\partial^2\varepsilon_3(h,k)}{\partial k\partial h}\,$

ez a (h,k)=(0,0)-ban:

$\partial_{21}f(u,v)=A_{12}+A_{21}\,$

mert a harmadrendűen kicsiny tagok a (h,k)=(0,0)-ban eltűnnek. Ugyanígy:

$\partial_{12}f(u,v)=A_{12}+A_{21}\,$

így ezek is egyenlők.