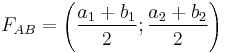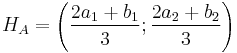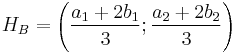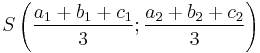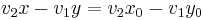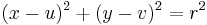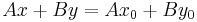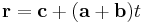11-edikes matek

Témák

OFI Tankönyv (Itt a "Megtekint"-ből lehet letölteni a pdf-et.)

Koordinátageometria

SZEPTEMBER

1. hét

1. heti feladatok Csapatok:

1. (Halacskás) Merőlegesség a koordinátarendszerben: OFI 180-180. oldal.

2. (Napocskás) Felezéspont, harmadolópont OFI 192-193. oldal.

3. (Dönci) A háromszög területe (csak "Dönci"): OFI 228-229. oldal.

4. (?) A kör egyenlete: OFI 202-205. oldal

5. (Holdacskás) Az egyenes irányvektoros egyenlete: OFI 214-215

6. (Láma) Ponthalmazok a koordinátarendszerben I., II. OFI 198-201. oldal.

7. (Ördögök) Súlypont: OFI 194-195.

2. hét

2. heti feladatok

3. hét

Felezéspont:

$F_{AB}=\left(\frac{a_1+b_1}{2};\frac{a_2+b_2}{2}\right)$

szlogen: "átlag"

Harmadolópont:

$H_{A}=\left(\frac{2a_1+b_1}{3};\frac{2a_2+b_2}{3}\right)$

$H_{B}=\left(\frac{a_1+2b_1}{3};\frac{a_2+2b_2}{3}\right)$

szlogen: "átlag, amiben a tz-t duplán számítjuk"

Párhuzamosság:

(a;b)-vel párhuzamos az (a;b) és a (-a;-b), de a (λa;λb) is.

Merőlegesség:

(a;b)-re merőleges a (-b;a) és a (b;-a) (vagy ezek lambdaszorosa)

3. heti feladatok

Példákhoz: Egy egyenes irányvektora olyan nemnulla vektor, ami párhuzamos az egyenessel. (Egy egyenesnek sok irányvektora tud lenni.) Egy oldal felezőmerőlegese, az az egyenes, ami áthalad az oldal felezéspontján és merőleges az oldalra.

Súlypont:

$S\left(\frac{a_1+b_1+c_1}{3};\frac{a_2+b_2+c_2}{3}\right)$

4. hét

Egy alakzat egyenlete egy olyan egyenlet, melyet egy (x,y) pont akkor és csak akkor tesz igazzá, ha rajta van az alakzaton.

Az egyenes egyenlete:

$v_2x-v_1y=v_2x_0-v_1y_0\,$

ahol (v₁,v₂) az egyenes egy irányvektora, (x₀,y₀) egy adott pontja. A kör egyenlete:

$(x-u)^2+(y-v)^2=r^2\,$

ahol (u,v) a kör középpontja, r a sugara.

OKTÓBER

1. hét

Gyakorlás:

Gyakorló

Dolgozat:

Koordinátageometria 1. A

Koordinátageometria 1. B

2. hét

Csoportok:

1. (Halacskás) Pont és alakzat távolsága: OFI 230-231. oldal.

2. (Napocskás) Egyenesek metszéspontja OFI 218-219. oldal.

3. (Dönci) Alapszerkesztések, egyenes egy pontjában merőleges, felezőmerőleges: OFI 220-223. oldal.

4. (Teki) Oldalfelező merőleges, oldalfelező merőlegesek metszéspontja, magasságpont: OFI 224-225.

5. (Holdacskás) A kör érintője: OFI 226. o.

6. (Lámás) Külső pontból merőleges, párhuzamos. OFI 202-205. oldal

7. (Ördögök) Magasságvonal, súlyvonal OFI 224-225.

Közös feladat: Studium Generale Koordinátageometria 1. oldal

Az egyenes paraméteres vektoregyenlete:

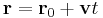$\mathbf{r}=\mathbf{r}_0+\mathbf{v}t$, (t∈R)

Az egyenes paraméteres egyenletrendszere:

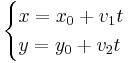$\begin{cases}x=x_0+v_1t\\y=y_0+v_2t\end{cases}$, (t∈R)

Az egyenes paramétermentes egyenlete:

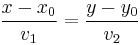$\frac{x-x_0}{v_1}=\frac{y-y_0}{v_2}\,$, v₁,v₂ ≠ 0

Az egyenes irányvektoros egyenlete:

$v_2x-v_1y=v_2x_0-v_1y_0\,$

Az egyenes normálvektoros egyenlete:

$Ax+By=Ax_0+By_0\,$

Feladat: Igazoljuk, hogy ha az a, b, c vektorok az ABC háromszög körül írt körének középpontjából indulnak a csúcsokhoz, akkor a magasságpontba az a + b + c vektor mutat.

Megoldás. A magasságvonalak vektoregyenletei:

$\mathbf{r}=\mathbf{c}+(\mathbf{a}+\mathbf{b})t$

$\mathbf{r}=\mathbf{b}+(\mathbf{a}+\mathbf{c})t$

$\mathbf{r}=\mathbf{a}+(\mathbf{b}+\mathbf{c})t$

mert pl. az a + b vektor az m_c egy irányvektora, hiszen |a|=|b|=R a körül írt kör sugara, azaz a és b rombuszt feszít ki, aminek az átlói merőlegesen felezik egymás és az a + b átlóvektor merőleges a c oldalra. De t=1 paraméterértéknél mindhárom fenti vektoregyenletben r = a + b + c, ami a magasságok metszéspontjába mutat, azaz a magasságpontba.

3. hét

Súlyvonal és magasságvonal.

A háromszög egy súlyvonalának nevezzük a csúcsot a szemközti oldal felezőpontjával összekötő egyenest.

A háromszög egy magasságvonalának nevezzük a csúcsból a szemközti oldalra bocsátott merőleges egyenest.

Feladatlap

Dolgozat

Feladatlap Feladatlap