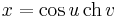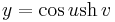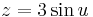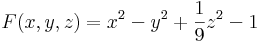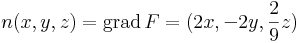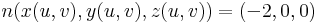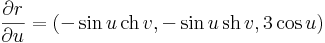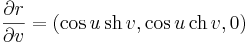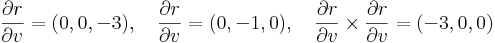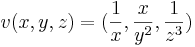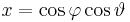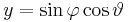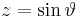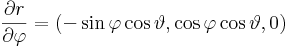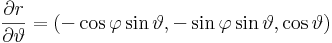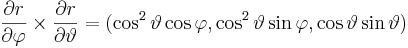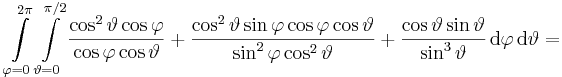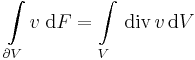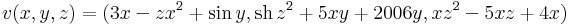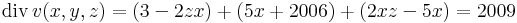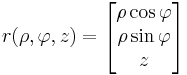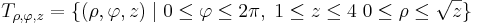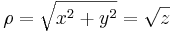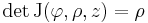A3 2009 gyak 1
Tartalomjegyzék |
Vonalintegrál
1. Integrálja a
vektormezőt az
görbe mentén!
Mo.
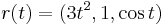
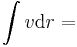
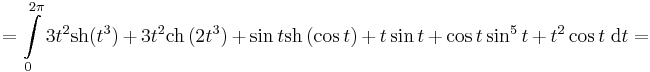
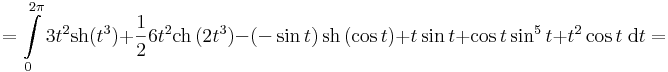
- itt
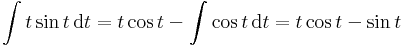
- és
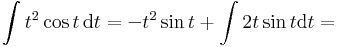
- itt
ezért
Rotációmentes vektormező, potenciál
Tétel Ha v(r) egy egyszeresen összefüggő tartományon értelmezett differenciálható függvény, amire rot v ≡ 0, akkor minden zárt görbére a vonalintegrálja 0.
Tétel (Konzervatív vektormezők jellemzése) v(r) egy egyszeresen összefüggő tartományon értelmezett folytonosa differenciálható függvény. Ekkor a következő három kijelentés ekvivalens egymással:
- rot v ≡ 0 (örvénymentes)
- minden zárt görbére a vonalintegrálja 0 (konzervatív)
- létezik Φ(r) folytonosan differenciálható skalárfüggvény, hogy grad Φ ≡ v (potenciálos)
Tétel (Első gradiens tétel) Ha a v(r) egy egyszeresen összefüggő tartományon értelmezett folytonosan differenciálható függvény potenciálos és Φ a potenciálja, akkor
Stokes-tétel Ha v egy folytonosan differenciálható vektormező és F olyan felület, mely peremével együtt a v értelmezési tartományában van, akkor
(megj.: ha G egy egyszeresen összefüggő tartománybeli zárt görbe, akkor mindig létezik olyan F felület ezen belül, melynek pereme G.)
2. Integráljuk a
vektormezőt az
görbe mentén!
Mo. A vektormező rotációmentes:
A görbe azonban nem zárt, így nem használhatjuk közvetlenül a Stokes-tételt. Két megoldási módot választhatunk.
(1) Kiegészítjük egy egyszerű görbével zárttá. A két végpont:
ezeket paraméter szerint növekvő módon az
Köti össze. Ekkor r+r2 már zárt és
(2) Megmondjuk a vektormező potenciálfüggvényét; ezt is vonalintegrállal. Tudjuk, hogy a rot v ≡ 0 miatt létezik Φ, amivel grad Φ = v és
Ezért legyen
Legyen a kezdőpont (0,0,0), a görbe:
Ezzel
Ellenőrizzük!
Ezzel a görbére a vonalintegrál:
- Φ( − 3,0,2) − Φ(3,0,2) = 12
Felületi integrál
3. Határozzuk meg az
felület normálvektorát a (u,v)=(π,0)-hoz tartozó pontban!
Mo. (1) Felírhatjuk például a görbét implicit alakban. Mivel
ezért
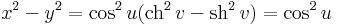
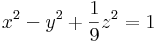 ill.
ill. 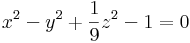
Ekkor az
gradiense a normálvektort adja:
azaz az adott pontban
(2) A felületi normálist a koordinátavonal irányú vektorok vektoriális szorzata is kiadja.
Az adott pontban:
4. Integráljuk a felső egységsugarú, origóközépponttú félgömbefelületre az
vektormezőt!
Mo. Paraméterezzük gömbi koordinátákkal: r(φ,θ)=(x(φ,θ),y(φ,θ),z(φ,θ))
A koordinátavonal irányú vektorok:
Az integrál:
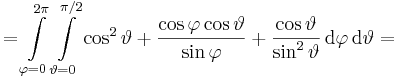
Gauss-tétel
Ha v folytonosan differenciálható vektormező és V az értelmezési tartományába eső kompakt térrész, melynek határa a ∂V felület, akkor
5. Számítsuk ki az
- x2 + y2 = z
felület z=1 és z=4 síkok közé eső darabjára a
vektormező felületmenti integrálját!
Mo. Vegyük észre, hogy a fedő és alaplapokon a vektormezőnek csak felületirányú komponense van, ezért ezeken a vektormező integrálja 0. A vektormező divergenciájának integrálja a térrészre tehát egyenlő lesz a palást felületi integráljával.
Beparaméterezve a forgástestet (áttérve hengerkoordinátákra)
és a tartomány:
hiszen
tudjuk, hogy a hengerkoordinátáknál:
ezért
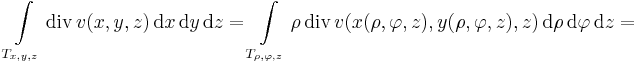
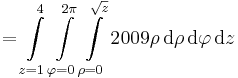
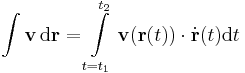
![v(x,y,z)=(\mathrm{sh}(y^2\sqrt[3]{x})+\mathrm{ch}\,(x+y^3),z\,\mathrm{sh}\,(\cos y)+yz,z^5+y^2)](/upload/math/5/5/3/553ca9b8ca0bf5a814d1ada9892b7d07.png)
![r(t)=(t^3,t,\sin t),\quad\quad t\in[0,2\pi]](/upload/math/b/4/4/b44634145192b4ccc45c6423bf4a50ef.png)
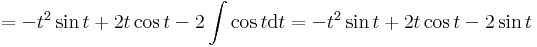
![=[\mathrm{ch}(t^3)]_0^{2\pi}+\frac{1}{2}[\mathrm{sh}\,(2t^3)]_0^{2\pi}-[\mathrm{ch}\,(\cos t)]_0^{2\pi}+](/upload/math/0/7/c/07cbc6914921034b3f7614bf4856fd22.png)
![+[t\cos t-\sin t]_0^{2\pi} +\frac{1}{6}[\sin^6t]_0^{2\pi}+[-t^2\sin t+2t\cos t-2\sin t]_0^{2\pi}=](/upload/math/1/c/1/1c17addd60523ef0c553f8578b9951b0.png)
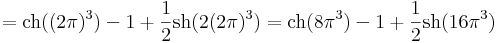
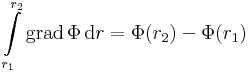
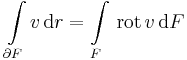
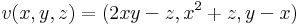
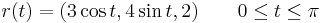
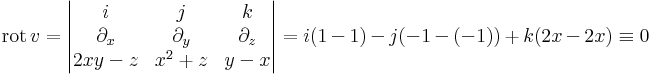
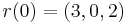
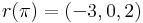
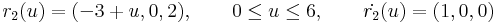
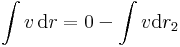
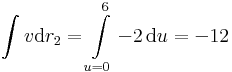
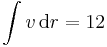
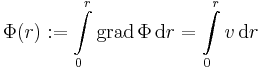
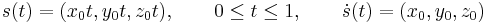
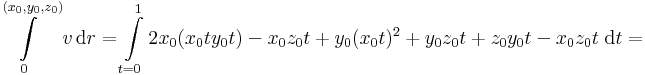
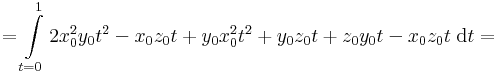
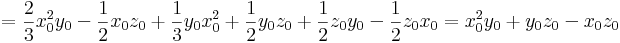
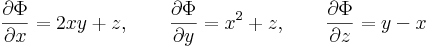
![r(u,v)=(\cos u\,\mathrm{ch}\,v,\cos u\,\mathrm{sh}\,v,3\sin u),\quad\quad (u,v)\in [0,4]\times [0,2]](/upload/math/7/4/c/74c56f94610e18ccfb7b3f950fd5b32a.png)