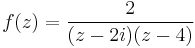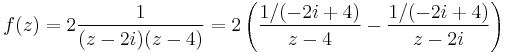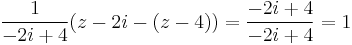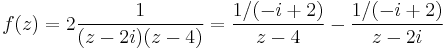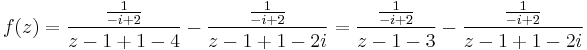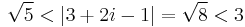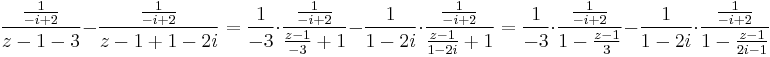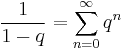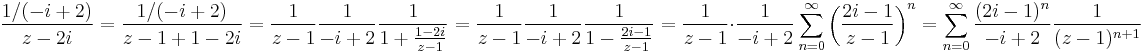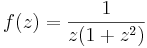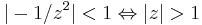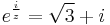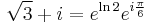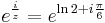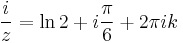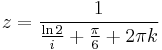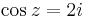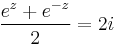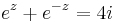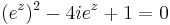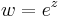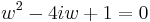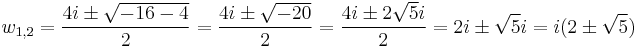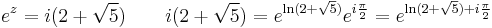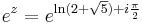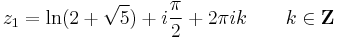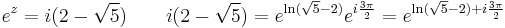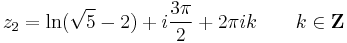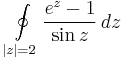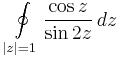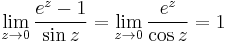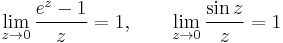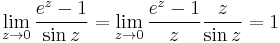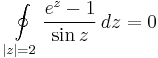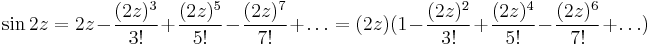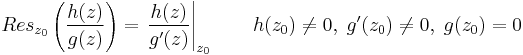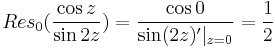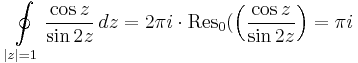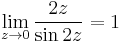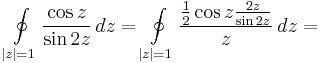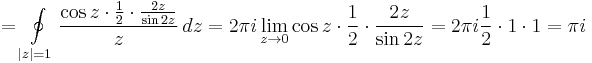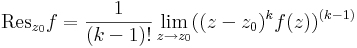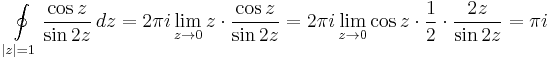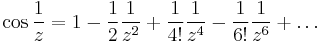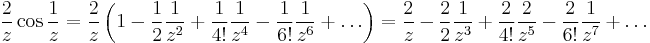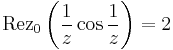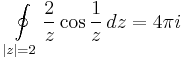A3 2016 gyak 2

Laurent-sorfejtés

1. a Határozzuk meg az

$f(z)=\frac{2}{(z-2i)(z-4)}$

függvény 1 körüli Laurent-sorait! Melyik sor állítja elő a függvényt a 3+2i pontban?

Mo. Parciális törtekre bontás. Mivel z-2i-(z-4)=-2i+4, ezért

$f(z)=2\frac{1}{(z-2i)(z-4)}=2\left(\frac{1/(-2i+4)}{z-4}-\frac{1/(-2i+4)}{z-2i}\right)$

és valóban, mert

$\frac{1}{-2i+4}(z-2i-(z-4))=\frac{-2i+4}{-2i+4}=1$

azaz

$f(z)=2\frac{1}{(z-2i)(z-4)}=\frac{1/(-i+2)}{z-4}-\frac{1/(-i+2)}{z-2i}$

A sort a z₀ = 1 körül kell sorba fejteni, azaz a z − 1 hatványai szerepelnek majd az összegben. Ehhez z-1-nek szerepelnie kell a nevezőkben:

$f(z)=\frac{\frac{1}{-i+2}}{z-1+1-4}-\frac{\frac{1}{-i+2}}{z-1+1-2i}=\frac{\frac{1}{-i+2}}{z-1-3}-\frac{\frac{1}{-i+2}}{z-1+1-2i}$

Két szingularitás: z = 4 és z = 2i. Ezeknek a távolsága a középponttól:

|1-4|=3 és

$|1-2i|=\sqrt{5}$.

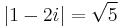A sorfejtés középpontja, az 1 körül tehát három olyan körgyűrű rajzolható, melyben reguláris lesz a függvény:

I.) |z-1|<|2i-1|, azaz $|z-1|<\sqrt{5}$

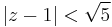
II.) |2i-1|<|z-1|<|4-1|, azaz 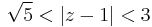$\sqrt{5}<|z-1|<3$ és

III.) 3<|z-1|.

A 3+2i pont a II. tartományba esik, mert a sorfejtés középpontjától való távolsága:

$\sqrt{5}<|3+2i-1|=\sqrt{8}<3$

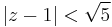I.) A $|z-1|<\sqrt{5}$ körlap,

melyen belül a sor reguláris és z − 1-nek csak nemnegatív hatványai szerepelnek a sorban. Ilyenkor "z − 1 melletti tagból csinálunk mértani sort":

$\frac{\frac{1}{-i+2}}{z-1-3}-\frac{\frac{1}{-i+2}}{z-1+1-2i}=\frac{1}{-3}\cdot\frac{\frac{1}{-i+2}}{\frac{z-1}{-3}+1}-\frac{1}{1-2i}\cdot\frac{\frac{1}{-i+2}}{\frac{z-1}{1-2i}+1}=\frac{1}{-3}\cdot\frac{\frac{1}{-i+2}}{1-\frac{z-1}{3}}-\frac{1}{1-2i}\cdot\frac{\frac{1}{-i+2}}{1-\frac{z-1}{2i-1}}$

Alkalmazva a

$\frac{1}{1-q}=\sum\limits_{n=0}^\infty q^n$

formulát, ha | q | < 1 a

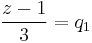$\frac{z-1}{3}=q_1$ és $\frac{z-1}{2i-1}=q_2$

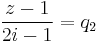
hányadosokra kapjuk:

$f(z)=\frac{1}{-3}\frac{1}{-i+2}\cdot\sum\limits_{n=0}^\infty\left(\frac{z-1}{3}\right)^n-\frac{1}{1-2i}\frac{1}{-i+2}\cdot\sum\limits_{n=0}^\infty\left(\frac{z-1}{2i-1}\right)^n=\sum\limits_{n=0}^\infty\frac{1}{3i-6}\cdot\left(\frac{1}{3}\right)^n(z-1)^n-\sum\limits_{n=0}^\infty\frac{1}{(1-2i)(-i+2)}\left(\frac{1}{2i-1}\right)^n(z-1)^n=\sum\limits_{n=0}^\infty\left(\frac{1}{3i-6}\cdot\left(\frac{1}{3}\right)^n-\frac{1}{(1-2i)(-i+2)}\left(\frac{1}{2i-1}\right)^n\right)(z-1)^n$

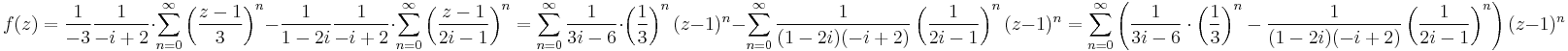
II.) A 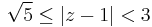$\sqrt{5}\leq|z-1|<3$ körgyűrű,

melyben az első tag reguláris, de a második már nem. Ilyenkor "a z-1-et emeljük ki a nevezőből":

$\frac{1/(-i+2)}{z-2i}=\frac{1/(-i+2)}{z-1+1-2i}=\frac{1}{z-1}\frac{1}{-i+2}\frac{1}{1+\frac{1-2i}{z-1}}=\frac{1}{z-1}\frac{1}{-i+2}\frac{1}{1-\frac{2i-1}{z-1}}=\frac{1}{z-1}\cdot\frac{1}{-i+2}\sum\limits_{n=0}^{\infty}\left(\frac{2i-1}{z-1}\right)^n=\sum\limits_{n=0}^{\infty}\frac{(2i-1)^n}{-i+2}\frac{1}{(z-1)^{n+1}}$

Tehát itt:

$f(z)=\sum\limits_{n=0}^\infty\frac{1}{3i-6}\cdot\left(\frac{1}{3}\right)^n(z-1)^n-\sum\limits_{n=0}^{\infty}\frac{(2i-1)^n}{-i+2}\frac{1}{(z-1)^{n+1}}$

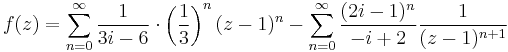
III.) Végül a |z-1|>3 körgyűrűn

$f(z)=\sum\limits_{n=0}^\infty\frac{1}{3i-6}\cdot\left(\frac{1}{z-1}\right)^{n+1}-\sum\limits_{n=0}^{\infty}\frac{(2i-1)^n}{-i+2}\frac{1}{(z-1)^{n+1}}$

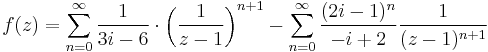
1. b Fejtsük sorba a 0 körül az

$f(z)=\frac{1}{z(1+z^2)}\,$

függvényt! Melyik sor állítja elő a függvényt az 1+2i-ben?

Mo. A szingularitások: 0, +i, -i. A sorfejtés középpontja, a nulla körül tehát két olyan körgyűrű rajzolható, melyben reguláris lesz a függvény: I.) 0<|z|<1 és II.) |z|>1. Az 1+2i pont a II. tartományba esik, mert 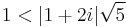$1<|1+2i|\sqrt{5}$. A függvényt nem kell parciális törtekre bontani, mert 1/z szorzótényezőként szerepel és a második tényező pont mértani sor alakú q=-z^2-tel.

I.) 0<|z|<1. "Ekkor az nevezőbeli 1-ból kell 1-et csinálni":

$f(z)=\frac{1}{z(1+z^2)}=\frac{1}{z}\frac{1}{1-(-z^2)}=\frac{1}{z}\sum\limits_{n=0}^\infty(-z^2)^n=\sum\limits_{n=0}^\infty(-1)^nz^{2n-1}$

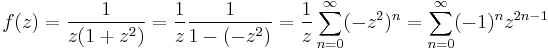
És a konvergencia tartománya valóban:

$|-z^2|<1\Leftrightarrow |z|<1$ ($z\ne 0$)

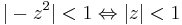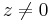II.) 1<|z|. "Ekkor az nevezőbeli z^2-ből kell 1-et csinálni":

$f(z)=\frac{1}{z}\cdot\frac{1}{z^2}\cdot\frac{1}{\frac{1}{z^2}+1}=\frac{1}{z}\cdot\frac{1}{z^2}\cdot\frac{1}{1-\frac{-1}{z^2}}=\frac{1}{z^3}\sum\limits_{n=0}^\infty\left(-\frac{1}{z^2}\right)^n=\sum\limits_{n=0}^\infty(-1)^nz^{-2n-3}$

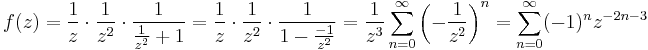
És a konvergencia tartománya valóban:

$|-1/z^2|<1\Leftrightarrow |z|>1$

Komplex egyenlet

2. a) Oldjuk meg az

$e^{\frac{i}{z}}=\sqrt{3}+i$

egyenletet!

Mo.

$\sqrt{3}+i=e^{\ln 2}e^{i\frac{\pi}{6}}$

mert a szöge 30 fok, a hossza 2. Ezért az egyenlet:

$e^{\frac{i}{z}}=e^{\ln 2 +i\frac{\pi}{6}}$

azaz

$\frac{i}{z}=\ln 2 +i\frac{\pi}{6}+2\pi i k$

$z=\frac{1}{\frac{\ln 2}{i} +\frac{\pi}{6}+2\pi k}$

2. b) Oldjuk meg a

$\cos z=2i\,$

egyenletet!

Mo.

$\frac{e^z+e^{-z}}{2}=2i$

$e^z+e^{-z}=4i\,$

$(e^z)^2-4ie^z+1=0\,$

$w=e^z\,$

$w^2-4iw+1=0\,$

$w_{1,2}=\frac{4i\pm\sqrt{-16-4}}{2}=\frac{4i\pm\sqrt{-20}}{2}=\frac{4i\pm 2\sqrt{5}i}{2}=2i\pm\sqrt{5}i=i(2\pm\sqrt{5})$

$e^{z}=i(2+\sqrt{5})\qquad i(2+\sqrt{5})=e^{\ln(2+\sqrt{5})}e^{i\frac{\pi}{2}}=e^{\ln(2+\sqrt{5})+i\frac{\pi}{2}}$

$e^{z}=e^{\ln(2+\sqrt{5})+i\frac{\pi}{2}}$

$z_1=\ln(2+\sqrt{5})+i\frac{\pi}{2}+2\pi i k\qquad k\in \mathbf{Z}$

$e^{z}=i(2-\sqrt{5})\qquad i(2-\sqrt{5})=e^{\ln(\sqrt{5}-2)}e^{i\frac{3\pi}{2}}=e^{\ln(\sqrt{5}-2)+i\frac{3\pi}{2}}$

$e^{z}=e^{\ln(\sqrt{5}-2)+i\frac{3\pi}{2}}$

$z_2=\ln(\sqrt{5}-2)+i\frac{3\pi}{2}+2\pi i k\qquad k\in \mathbf{Z}$

Reziduum és körintegrál

4. a)

$\oint\limits_{|z|=2}\frac{e^z-1}{\sin z}\,dz$

b)

$\oint\limits_{|z|=1}\frac{\cos z}{\sin 2z}\,dz$

c)

$\oint\limits_{|z|=2}\frac{2}{z}\cos \frac{1}{z}\,dz$

Mo. a) Szingularitásai: 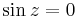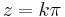$\sin z=0\,$; $z=k\pi\,$, tehát a körön belül csak a z=0-ban szakad. Mivel a számláló és a nevező is 0 a nullában, ezért a L'H-lal kiszámítható a határértéke, ha van. L'H-lal:

$\lim\limits_{z\to 0}\frac{e^z-1}{\sin z}=\lim\limits_{z\to 0}\frac{e^z}{\cos z}=1$

Vagy

$\lim\limits_{z\to 0}\frac{e^z-1}{z}=1,\qquad \lim\limits_{z\to 0}\frac{\sin z}{z}=1$

miatt

$\lim\limits_{z\to 0}\frac{e^z-1}{\sin z}=\lim\limits_{z\to 0}\frac{e^z-1}{z}\frac{z}{\sin z}=1$

Tehát megszüntethető a szingularitás. Ez a függvény megtévesztésig hasonlít egy reguláris függvényre, azaz az integrálja a Cauchy-integráltétel miatt 0. Vagy reguláris a 0-n kívül, a körön belül és mivel ott megszüntethető a szingularitás, ezért nincs a Laurent-sorában főrész, azaz nincs 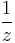$\frac{1}{z}$-s tag. Emiatt 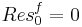$Res_0^f=0$. Innen:

$\oint\limits_{|z|=2}\frac{e^z-1}{\sin z}\,dz=0$

b) Szingularitásai: 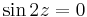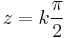$\sin 2z=0\,$; $z=k\frac{\pi}{2}\,$, tehát a körön belül csak a z=0-ban szakad. Itt cos(0) = 1 és

$\sin 2z=2z-\frac{(2z)^3}{3!}+\frac{(2z)^5}{5!}-\frac{(2z)^7}{7!}+\dots=(2z)(1-\frac{(2z)^2}{3!}+\frac{(2z)^4}{5!}-\frac{(2z)^6}{7!}+\dots)$

azaz pólusszingularitása van és elsőfokú pólusa van a nullában. Ezt onnan tudjuk, hogy 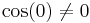$\cos(0)\ne 0$, és a nevező gyöktényezőjét, 2z-t az első hatványon lehet a legmagasabb hatványon kiemelni a sorból.

1. megoldás. Alkalmazhatjuk tehát az elsőrendű pólus reziduumának képletét:

$Res_{z_0}\left(\frac{h(z)}{g(z)}\right)=\left.\frac{h(z)}{g'(z)}\right|_{z_0}\qquad h(z_0)\ne 0, \;g'(z_0)\ne 0,\;g(z_0)=0$

$Res_0(\frac{\cos z}{\sin 2z})=\frac{\cos 0}{\sin(2z)'|_{z=0}}=\frac{1}{2}$

Innen a reziduumtétellel:

$\oint\limits_{|z|=1}\frac{\cos z}{\sin 2z}\,dz=2\pi i \cdot\mathrm{Res}_0(\left(\frac{\cos z}{\sin 2z}\right)=\pi i$

2. megoldás. C.i.f.-fel. Felhasználva, hogy

$\lim\limits_{z\to 0}\frac{2z}{\sin 2z}=1$

$\oint\limits_{|z|=1}\frac{\cos z}{\sin 2z}\,dz=\oint\limits_{|z|=1}\frac{\frac{1}{2}\cos z\frac{2z}{\sin 2z}}{z}\,dz=$

a számlálóban reguláris, a nevezőben elsőfokú, azaz a nulladik deriváltra vontkozó Cauchy-integrálformulából:

$=\oint\limits_{|z|=1}\frac{\cos z\cdot \frac{1}{2}\cdot\frac{2z}{\sin 2z}}{z}\,dz=2\pi i\lim\limits_{z\to 0}\cos z\cdot \frac{1}{2}\cdot\frac{2z}{\sin 2z}=2\pi i\frac{1}{2}\cdot 1\cdot 1=\pi i$

3. megoldás. Az általános reziduumszámítós képlettel. k-adfokú pólus esetén

$\mathrm{Res}_{z_0}f=\frac{1}{(k-1)!}\lim\limits_{z\to z_0}((z-z_0)^k f(z))^{(k-1)}$

Most k=1, azaz k-1=0, azaz nem kell deriválni, csak határértéket számítani:

$\oint\limits_{|z|=1}\frac{\cos z}{\sin 2z}\,dz=2\pi i\lim\limits_{z\to 0}z\cdot\frac{\cos z}{\sin 2z}=2\pi i\lim\limits_{z\to 0}\cos z\cdot\frac{1}{2}\cdot \frac{2z}{\sin 2z}=\pi i$

c) Csak a 0-ban szakad (de ott nagyon). Laurent-sorba fejtve 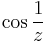$\cos \frac{1}{z}$-t:

$\cos \frac{1}{z}=1-\frac{1}{2}\frac{1}{z^2}+\frac{1}{4!}\frac{1}{z^4}-\frac{1}{6!}\frac{1}{z^6}+\dots$

azaz a Laurent-sor főrészében végtelen sok tag van, ez azt jelenti, hogy függvénynek a nullában lényeges szingularitása van. Ilyen függvény integrálját reziduumtétellel szoktuk kiszámítani. Innen:

$\frac{2}{z}\cos \frac{1}{z}=\frac{2}{z}\left(1-\frac{1}{2}\frac{1}{z^2}+\frac{1}{4!}\frac{1}{z^4}-\frac{1}{6!}\frac{1}{z^6}+\dots\right)=\frac{2}{z}-\frac{2}{2}\frac{1}{z^3}+\frac{2}{4!}\frac{2}{z^5}-\frac{2}{6!}\frac{1}{z^7}+\dots$

Leolvasva a reziduumot, az 1/z együtthatója:

$\mathrm{Rez}_0\left(\frac{1}{z}\cos \frac{1}{z}\right)=2$

$\oint\limits_{|z|=2}\frac{2}{z}\cos \frac{1}{z}\,dz=4\pi i$