Informatics1-2018/HW6
Tartalomjegyzék |
1. Exercise
3 points
The Collatz or 3n+1 problem is the following:
- Let n be a positive integer.
- Let g(n) = n/2 is n is even and 3n+1 is odd.
- Then one can iterate g over-and-over for any given number. For example starting with 98:
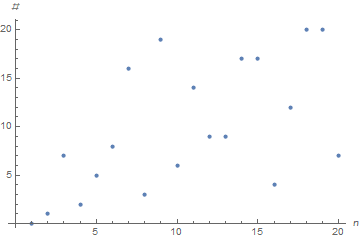
{98, 49, 148, 74, 37, 112, 56, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1}
It is an interesting and unproven conjecture that starting from any number, you will reach 1 sooner or later. In the example above it took 25 steps. For example 5 -> 16 -> 8 -> 4 -> 2 -> 1 takes 5 steps.
Plot the number of steps needed to reach one against n, use ListPlot and n=1...1000
2. Exercise
a)
3 points
Define a function T with three arguments:
- f a function
- n a natural number
- x0 a real number
For this values calculate the nth Taylor polynomial of f around x0.
For example:
In[1]:= T[Exp,4,0] Out[1]:= 1 + x + x^2/2 + x^3/6 + x^4/24
Note that there is a buit-on function Series which does exactly this, but don't use that, implement it on your own! Use the sum symbol from the paletta and the Derivative.
b)
3 points
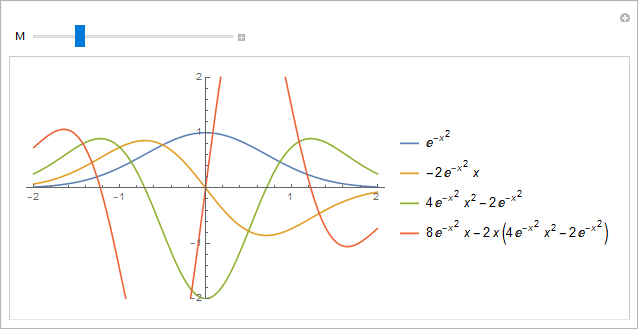
Plot the function 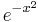 and its derivatives on a single Plot.
For a given M, plot
and its derivatives on a single Plot.
For a given M, plot 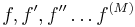 on the interval [ − 2,2] (this is M+1 functions in total).
Use Manipulate to set the value of M.
on the interval [ − 2,2] (this is M+1 functions in total).
Use Manipulate to set the value of M.
Handing in
Deadline: 2018.11.25 23:59
Attach the solution notebook file to the email named like this (use your own login, not mine):
A1_borbely_HW6.nb