Informatics2-2019/HW8
Tartalomjegyzék |
numpy Homework
Implement the following python functions. The name of the exercise should be the name of the function.
You will need import numpy! On your own computer I recommend Anaconda because it is installed with numpy by default. Mind that you need the 2.7 version.
Or you can use the leibniz.
matrix (2p)
The function should have 3 parameters, one matrix and two indices:
M: a matrix i: a row index j: a column index
The output should be a matrix (let's call A) with the same size as M. It should be the outer product of the ath row and the ath column of M. In formula:
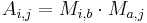
You can calculate this kind of product of vectors by multiplying a somethig-by-1 and a 1-by-something matrix.
derivative (3p)
The function should have 3 parameters, two real numbers and one integer:
a: the left-hand-side of the interval b: the right-hand-side of the interval n: the number of uniformly distributed points in the interval
a < b and n > 1.
- The output should be a numpy vector of length n-2 containing the numerical derivative of the function
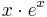 on the given interval, except the endpoints.
on the given interval, except the endpoints.
- Use the following estimation for the derivative (more about numerical differentiation):
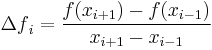
Handing-in
Send the exercises as a python code from your math email account to info1hazi@gmail.com
You should attach one python file containing the definition of the required functions without any test code or print command.
The file should be named:
EN1_HW8_<user account>.py
the subject of the letter should be the same (without the extension). For me example:
EN1_HW8_borbely.py
Deadline
12th of May, 29:59