Informatika1-2013/ZH2Gyakorlo

A gyakorló feladatok nem feltétlen tükrözik a ZH feladatainak nehézségét, de mindenképp jó gyakorlásnak számítanak a ZH-ra.

• Keresd meg a következő kódban található hibákat. (4 hiba van benne.)

def prim(n):
    s = 0
    for p in range(n):
        if is_prime(p) = True:
            s += 1
    L = ()
    i = 0
    psz = 0
    while psz < s:
        if is_prime(i)
            L.append[i]
            psz = psz + 1
        i = i + 1
    return L

• Írj Sage függvényt, mely a kapott x pozitív egész számot, ha páratlan megszorozza 3-al és hozzáad 1-et, ha páros elosztja 2-vel, majd kiírja az így kapott eredményt, és ezt addig folytatja amíg el nem jut 1-ig. (El fog jutni 1-ig, ez a Collatz sejtés.) A kiegészitendő részeket jelölik a <1>, <2>, <3>, <4>.

def collatz(x):
    <1> x > 1:
        if <2>:
            x = x / 2
        <3>:
            <4>
        print x

• Mit ír ki az alábbi kód?

d = {}
i = 0
while i < 10:
    d[i ** 2] = i
    i = i + 2
L = d.keys()
L.sort()
print L

• Írj Sage kódot amely ábrázolja a 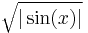$\sqrt{|\sin(x)|}$ függvényt piros színnel, és az x²cos(x) függvényt sárga színnel, a − π,π intervallumon, közös grafikonon. (Az abszolút érték függvény Sage-ben az abs(x))

• Írj olyan osztoszam(L, n) Sage függvényt, mely visszaadja, hogy az L egész számokat tartalmazó listának hány eleme osztja az n egész számot.

• Írj olyan hatvany(n) Sage függvényt, mely visszaadja azt a legnagyobb kitevőt melyre az n számot emelve a hatvány még 100 alatt marad.

• Mutass példát a find_root és a sum használatára, a Sage válaszával együtt!

• Mit ad ki az expand((a + b) ** 2) parancs? Hogyan kell az a és b változókat definiálni hogy ez működjön?

• Egy táskába pakolunk sorban elemeket, egészen addig amíg meg nem halad egy adott súlyt, amint meghaladta befejezzük a pakolást. Írj olyan pakol(L1, n) Sage függvényt, mely visszaadja a súlyt ahol megállt, L1 listában találhatók sorban az elemek súlyai, n a súly korlát. (A listában összesen nehezebb dolgok vannak mint a súly korlát, így nem kell figyelnünk túlindexelésre.)

• Futtassátok le a BFS és DFS algoritmust ezen a gráfon. Arra figyeljetek, hogy mindkét algoritmus, lexikografikusan vegye a szomszédokat, tehát, ha egy x csúcsnak y és z a szomszédja, akkor y-t dolgozza fel elõbb.