Informatika2-2014/Eloadas Python/1ZH

1. ZH

1. Írjunk fel egy reguláris kifejezést, mely pontosan azokra a két számból álló karakterláncokra illeszkedik, melyek oszthatók 3-mal. A reguláris kifejezés tehát illeszkedjen a "00", "03", "12", "24", "99" karaterláncokra, de ne illeszkedjen a "01", "98", "0a", "ab" karakterláncokra (az egyszerűség kedvéért az előtte lévő és az utána következő karakterekkel nem kell foglalkozni).

Megoldás

[0369][0369]|[147][258]|[258][147]

2. Írjunk kódot, mely egy karakterláncból mozaikszót képez. A mozaikszó a karakterlánc minden nagy betűvel kezdődő szavából csak a nagy betűk megtartásával képződik. A karakterlánc csak az angol ábécé betűit és szóközöket tartalmaz. Használjuk a 're' modul 'sub' függvényét, vagy egy regexp objektum 'sub' metódusát a megoldáshoz. A kód példa bemenetekre adott válaszai: \pont2

"American Mathematical Society" --> "AMS"

"Masters of Business Administration" --> "MBA"

Két megoldás

>>> import re
>>> line = 'Masters of Business Administration'
>>> prog = re.compile("[^A-Z]")
>>> prog.sub("", line)
'MBA'

>>> import re
>>> line = 'Masters of Business Administration'
>>> re.sub("[^A-Z]", "", line)
'MBA'

Két másik megoldás

>>> import re
>>> line = 'Masters of Business Administration'
>>> prog = re.compile("([A-Z])[a-z ]+")
>>> prog.sub(r"\1", line)
'MBA'

>>> import re
>>> line = 'Masters of Business Administration'
>>> re.sub("([A-Z])[a-z ]+", r"\1", line)
'MBA'

3. Egy file-ban soronként vannak a neptunkód--pontszám párok, szóközzel elválasztva. Írjunk python kódot, mely beolvassa ezt a file-t és egy szótárban tárolja a hallgatók eredményeit. A szótár kulcsai neptunkódok, az értékek ZH pontok.

Megoldás

f = open("eredmenyek.txt", "r")
 
d = {}
for line in f:
    l = line.split()
    d[l[0]] = int(l[1])
 
print d

4. Írjunk egy legjobbak nevű függvényt, mely egy -- az előző feladat szerinti -- szótárat és egy pozitív egész számot kap paraméterként. A függvény egy listában visszaadja az n legmagasabb pontszámú hallgató neptunkódját tetszőleges sorrendben, ahol n a második paraméter. Nincs két hallgató azonos pontszámmal.

Megoldás

pontszamok = {'C3WRGQ':15, 'PTKFGS':54, 'TB7RU9':65, 'YTMND1':43, 'BATMAN':78}
 
def legjobbak(pontDict, n):
    retval = []
    p = pontDict.values()
    p.sort()
    p = p[-n:]
    for k in pontDict:
        if pontDict[k] in p:
            retval.append(k)
    return retval
 
print legjobbak(pontszamok, 3)

5. Adjuk meg, hogy mely változók lesznek elérhetők az a és b objektumokból az alábbi kód futtatása után.

class A(object):
 
    x = 1
    z = 2
    def __init__(self):
        self.u = 6
        self.w = 4
 
class B(A):
 
    y = 5
    def __init__(self):
        self.v = 3
 
a = A()
b = B()

Megoldás

Az a objektumban elérhető a.x, a.z, a.u, a.w

A b objektumban elérhető b.x, b.z, b.y, b.v

6. Egészítsd ki az alábbi kódot. Az osztály egy téglatestet reprezentál, melynek surface tulajdonsággal lehet lekérni a felszínét.

Megoldás

import math
 
class Cuboid(object):
 
    def __init__(self, sideA, sideB, sideC):
        self.a = sideA
        self.b = sideB
        self.c = sideC
 
    @property
    def surface(self):
        return 2 * (self.a*self.b + self.a*self.c + self.b*self.c)

Használata:

>>> t = Cuboid(3, 4, 5)
>>> print t.surface
94

7. A Cube osztály a fenti Cuboid leszármazottja, mely a kockákat írja le.

• Egészítsük ki az '__init__' metódusát, hogy annak a 'self'-en kívül csak egy argumentuma legyen.
• Legyen volume (térfogat) írható és olvasható tulajdonsága. (Köbgyökhöz használjuk a python ** operátorát tört kitevővel.)

Egyszerű megoldás

import math
 
class Cube(Cuboid):
 
    def __init__(self, side):
        Cuboid.__init__(self, side, side, side)
 
    def __get_volume(self):
        """Calculates the 'volume' property."""
        return self.a ** 3
 
    def __set_volume(self, volume):
        """Sets the 'volume' property."""
        self.a = self.b = self.c = volume ** (1.0 / 3.0)
 
    volume = property(__get_volume, __set_volume,
                    doc="""Gets or sets the volume of the cube.""")

Megoldás, melyben a cube osztály leszármazott osztályaiban is átírható lesz a __get_volume és a __set_volume függvény, mivel a property függvény csak implicit függvényekre hat:

class Cube(Cuboid):
 
    def __init__(self, side):
        Cuboid.__init__(self, side, side, side)
 
    def __get_volume(self):
        """Calculates the 'volume' property."""
        return self.a ** 3
 
    def ___get_volume(self):
        """Indirect accessor for 'volume' property."""
        return self.__get_volume()
 
    def __set_volume(self, volume):
        """Sets the 'volume' property."""
        self.a = volume ** (1.0 / 3.0)
        self.b = self.a
        self.c = self.a
 
    def ___set_volume(self, volume):
        """Indirect setter for 'volume' property."""
        self.__set_volume(volume)
 
    volume = property(___get_volume, ___set_volume,
                    doc="""Gets or sets the volume of the cube.""")

E megoldások használata:

>>> k = Cube(4)
>>>> print k.surface
96
>>> print k.volume
64
>>> k.volume = 8
>>> print k.a
2.0

8. Egészítsük ki az alábbi kódot, hogy a megfelelő kimenetet produkálja:

Megoldás

>>> def egysegvektor(dim = 2, e = 1):
...     l = []
...     for i in range(dim):
...         l.append(0)
...     l[e-1] = 1
...     return l
... 
>>> print egysegvektor(4, 2)
[0, 1, 0, 0]
>>> print egysegvektor(5, 4)
[0, 0, 0, 1, 0]
>>> print egysegvektor(3, 1)
[1, 0, 0]
>>> print egysegvektor(2)
[1, 0]
>>> print egysegvektor(3)
[1, 0, 0]
>>> print egysegvektor()
[1, 0]

9. Mely adattípusoknak létezik hash értéke?

Megoldás

Létezik: int bool float tuple string

Nem létezik: list dict

10. Mit írnak ki a következő kódok?

Megoldás

>>> print [(x, y) 
...          for y in range(5) 
...          for x in range(5) 
...          if abs(x - y) == 1]
[(1, 0), (0, 1), (2, 1), (1, 2), (3, 2), (2, 3), (4, 3), (3, 4)]

>>> print [p for p in range(30) 
...          if len([x for x in range(1, p + 1) 
...                    if p % x == 0]) == 2]
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]

>>> print map(lambda x: x * 2, [1, 2, 5])
[2, 4, 10]

11. A kvaterniók a komplex számtest bővítésével kapott algebrai struktúra elemei. Hasonlóan ahhoz, ahogy a komplex számokat az $R^2$ elemeivel, a kvaterniókat $R^4$ elemeivel reprezentálhatjuk. A kvaterniók szokásos reprezentációja: a+bi+cj+dk, ahol i, j és k imaginárius egységek és a, b, c, d eleme R (továbbá i^2=j^2=k^2=-1, ij=k, jk=i, ki=j).

Írjunk egy Quaternion nevű osztályt, melynek példányai kvaterniók. Az osztálydefinícióban szerepeljen az alábbi 4 metódus:

• __init__: a q = Quaternion(a,b,c,d) kód hatására létrehozza az a+bi+cj+dk kvaterniót (egy kvaterniót 4 tulajdonság fogja jellemezni).
• __add__: összead két kvaterniót. A kvaterniók összeadása megfelel a 4-dimenziós vektorok összeadásának.
• __mul__: összeszoroz két kvaterniót. A szorzás szabálya: 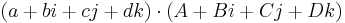$(a+bi+cj+dk)\cdot(A+Bi+Cj+Dk)$ szorzat értéke

aA − bB − cC − dD + (aB + bA + cD − dC)i + (aC − bD + cA + dB)j + (aD + bC − cB + dA)k

• __repr__: a (format metódus segítségével) a kvaterniót az $a+bi+cj+dk$ alaknak megfelelően írja ki. Például a q = Quaternion(1.1, 2.3, -3, 4.6) kvaternió megjelenítése 1.10000+2.30000i-3.00000j+4.60000k.

Megoldás

class Quaternion(object):
    """Calculating with quaternion"""
    def __init__(self, a, b, c, d):
        self.re, self.i, self.j, self.k = a, b, c, d
 
    def __add__(self, q):
        return Quaternion(self.re+q.re, self.i+q.i, self.j+q.j, self.k+q.k)
 
    def __mul__(self, q):
        a, b, c, d = self.re, self.i, self.j, self.k
        A, B, C, D = q.re, q.i, q.j, q.k
        return Quaternion(a*A - b*B - c*C - d*D,
                          a*B + b*A + c*D - d*C,
                          a*C - b*D + c*A + d*B,
                          a*D + b*C - c*B + d*A)
 
    def __repr__(self):
        return "{:.5f}{:+.5f}i{:+.5f}j{:+.5f}k".format(self.re, self.i, self.j, self.k)

Használata:

>>> q1 = Quaternion(1, 2, 3, 4)
>>> q2 = Quaternion(-1, 2, 0, -4)
>>> print q1
1.00000+2.00000i+3.00000j+4.00000k
>>> print q2
-1.00000+2.00000i+0.00000j-4.00000k
>>> q1 + q2
0.00000+4.00000i+3.00000j+0.00000k