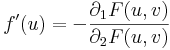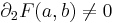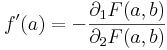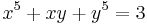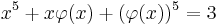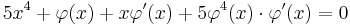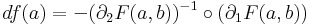Matematika A2a 2008/12. gyakorlat
Tartalomjegyzék |
Implicitfüggvény
Az egyenlettel megadott függvények esetén olyankor is ki tudjuk számítani a derivált értékét (adott pontban), ha nem rendezzük y-ra az egyenletet. Persze ekkor fel kell tennünk, hogy legalább elivleg kifejezhető y az egyeneltből és a kifejezés, amit kapunk differenciálható.
Az
egyenlet által meghatározott implicit függvénynek nevezzük azt az
függvényt melyre minden x ∈ H-ra:
Példa. Deriváljuk az
- x2 + y2 = 1
egyenlettel megadott differenciálható implicit függvényt!
Mo. A (-1,0) és az (1,0) pontokat tartalmazó részhamazokon nem lesz differenciálható implicit függény, de az ezeket nem tartalmazó intervallumokon igen. Az y-t az x függvényének tekintve: y=y(x)
- x2 + y(x)2 = 1
deriválva mindkét oldalt
visszaírva y-ra:
a derivált.
Általában, ha van differenciálható implicitfüggvény, akkor az alábbaikat állíthatjuk:
Tétel. Ha F:I×J  R téglalapon értelmezett, differenciálható függvény, létezik az F(x,y)=0 egyenletnek y: I
R téglalapon értelmezett, differenciálható függvény, létezik az F(x,y)=0 egyenletnek y: I  J differenciálható implicit függvénye és
J differenciálható implicit függvénye és
minden x∈I-re, akkor
Ui., Ekkor
ezt differenciálva (az összetett függvény deriválására vonatkozó képlettel)
azaz
Vegyük észre, hogy a fenti példában a kritikus pontokban ∂y(x2+y2)=0.
Tétel. Természetesen a fenti képlet akkor is felírható, ha F két többdimenziós téglalap szorzatán van értelmezve, de diffható, létezik a differenciálható implicit függvény és az F függvény y szerinti deriváltja nem nulla.
Legyen F:Rn×Rm Rm folytonosan differenciálható és tekintsük az F(x,y) = 0 egyenletet! Ha det(∂y)F ≠ 0, akkor (x,y)-ban létezik differenciálható y implicitfüggvénye F-nek és
Rm folytonosan differenciálható és tekintsük az F(x,y) = 0 egyenletet! Ha det(∂y)F ≠ 0, akkor (x,y)-ban létezik differenciálható y implicitfüggvénye F-nek és
Példa. Paraméterezzük az alábbi egyenletrendszer által meghatározott halmazt!
Itt az (x,y)-t szeretnénk kifejezni z-vel:
Implicit megadású függvényről akkor beszélünk, amikor egy függvény megadása nem (az explicit módon) y = f(x) alakban történik, hanem az x és y kapcsolatát egy mindkét változót tartalmazó
egyenlet írja le. Például adjunk meg olyan függvényt, melynek grafikonja valamely kör egy szakasza. Az
egyenletű körből könnyű az y változót kifejezni, az 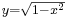 és
és 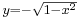 alakokat kapjuk. Bonyolultabb esetekben, például a
alakokat kapjuk. Bonyolultabb esetekben, például a
esetén semmi reményünk, hogy az y változóra valamilyen egyenletrendezéssel általános képletet kapjunk. Az ilyen példák miatt nevezik ezeket a típusú függvényeket implicit, avagy régi, választékos kifejezéssel élve bennrekedt függvényeknek. A differenciálszámítás szempontjából megelégedhetünk azzal, ha az implicit függvény deriváltját ki tudjuk számolni. Sok esetben ebből már következtethetünk a függvényre vagy annak viselkedésére is.
A modern analízis szemszögéből egy N × M  K normált terek között ható F függvény a ∈ N és b ∈ M pontokhoz tartozó implicit függvényén olyan, az a egy U környezetén értelmezett és a b egy V környezetébe képező f:U
K normált terek között ható F függvény a ∈ N és b ∈ M pontokhoz tartozó implicit függvényén olyan, az a egy U környezetén értelmezett és a b egy V környezetébe képező f:U  V függvényt értünk, melyre f(a)=b és minden x ∈ U pont esetén rendelkezik az
V függvényt értünk, melyre f(a)=b és minden x ∈ U pont esetén rendelkezik az
tulajdonsággal. Amelyet szavakban úgy fogalmazhatunk meg, hogy az F(x,y)=0 egyenletből az y változó kifejezhető y=f(x) alakban.
Most szorítkozzunk csak a kétváltozós esetre és tegyük fel, hogy létezik differenciálható implicit függvénye a differenciálható F függvénynek. Ekkor az F(x,y) függvény implicit függvénye az f(x), ha egy adott (u,v) pontban:
- F(u,v)=0 és
- minden az f értelmezési tartományába eső x-re F(x,f(x))≡0 és
- f(u)=v,
akkor világos, hogy ha
- 0 ≡ φ(x) = F(x,f(x)) = (F
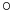 (id,f))(x) ,
(id,f))(x) ,
akkor
- φ'(x) ≡ 0
így tehát a függvénykompozíció deriválásának szabálya szerint:
így
Implicitfüggvény tétel
Tétel – Implicitfüggvény-tétel R-beli implicit függvényre – Legyen F az R2 egy részhalmazán értelmezett, R-be képező differenciálható függvény, mely az értelmezési tartománya egy (a,b) belső pontjában folytonosan differenciálható, F(a,b) = 0 és
(azaz (a,b)-ben az y szerinti parciális deriváltja nem nulla).
Ekkor van a-nak olyan I és b-nek olyan J környezete, hogy F-nek egyértelműen létezik az (a,b) párhoz tartozó f: I  J implicit függvénye, mely erősen differenciálható a-ban és deriváltja:
J implicit függvénye, mely erősen differenciálható a-ban és deriváltja:
Vázlatos bizonyítás. I. Először megkonstruáljuk az y=y(x) függvényt. Létezik olyan I × J ⊆ Dom(F) az (a,b) körül, hogy ∂2F sehol sem nulla, azonos előjelű -- sőt feltehetjük, hogy pozitív. Ez amiatt van, hogy ∂2F(a,b) ≠ 0 és ∂2F folytonos.
Az y=y(x) implicit függvény létezése egyenértékű azzal, hogy
- minden x ∈ I-re az F( x , . ) parciális függvénynek zérushelye van J-ben,
hiszen ekkor minden x-hez létezik olyan y ∈ J, hogy F(x,y)=0. Belátjuk, hogy minden ilyen x-hez egyetlen zérushelye van F( x , . )-nek.
Tekintsük a folytonos F( a , . ) parciális függvényt. A pozitívra választott y-szerinti deriváltból következik, hogy ez I-n szigorúan monoton növekvő. Mivel b-ben zérushelye van ( F(a,b)=0 ), ezért van olyan y2 > b pont, hogy ott F( a , . ) pozitív és y1 < b pont, hogy ott F( a , . ) negatív. Ekkor F folytonossága miatt van az (a,y1) pontnak olyan környezete, ahol F negatív és van az (a,y2) pontnak olyan környezete, ahol F pozitív. Most definiáljuk át I-t és J-t úgy, hogy I × J-n az F egy J-beli elem fölött mindenhol pozitív, egy J-beli elem alatt mindehol negatív értéket vegyen föl.
A praciális deriváltak folytonosságából az is következik, hogy minden x ∈ I-re az F( x , . ) függvény is szigorúan monoton növekvő, negatív és pozitív értéket is felvevő folytonos függvény, így a Bolzano-tétel alapján létezik yx zérushelye és mindegyiknek egyetlen zérushelye létezik.
II. Állítjuk, hogy a φ:I  J, x
J, x  yx függvény implicit függvénye F-nek, azaz minden x ∈ I-re F(x,φ(x))=0.
yx függvény implicit függvénye F-nek, azaz minden x ∈ I-re F(x,φ(x))=0.
Könnyen belátható, hogy φ folytonos a-ban, hiszen ha a-hoz közeledve mindig találnánk olyan x pontot, hogy φ(x) egy adott ε-nál mindig jobban eltér b-től, akkor φ(x) egy olyan környezetbe esne bele, ahol F mindenhol egy pozitív számnál nagyobb vagy mindenhol egy negatív számnál kisebb. Ám, F(x,φ(x))=0, így ez ellentmondana F folytonos tulajdonságának.
III. Végül az implicit függvény differenciálható a-ban, mert ha van (a,b)-ben érintősík, akkor az az érintőegyenesben metszi az [x,y] síkot.
Példák
Tekintsük a következő egyenletű síkgörbét:
Nem lenne könnyű feladat kifejezni belőle y-t, mert az ötödfokú egyenletnek nincs általános megoldóképlete. Mivel a baloldal akárhányszor differenciálható, ezért joggal feltételezhetjük, hogy bizonyos pontokban létezik implicit függvénye. Tegyük fel, hogy φ ilyen függvény. Ekkor az egyenlet
alakú, melynek minden olyan x-nél, ahol φ differenciálható:
ahonnan a derivált:
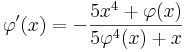 vagy szimbolikusan:
vagy szimbolikusan: 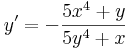 .
Alaposabb vizsgálatokkal kideríthető, hogy ez a derivált minden pontban létezik és negatív, így az implicit függvény mindenhol létezik és szigorúan monoton csökkenő. Vegyük észre, hogy a nevezőben lévő kifejezés pont ∂yF(x,y) és az implicit függvény létezésének feltétele pont a nevező nullától különböző volta.
.
Alaposabb vizsgálatokkal kideríthető, hogy ez a derivált minden pontban létezik és negatív, így az implicit függvény mindenhol létezik és szigorúan monoton csökkenő. Vegyük észre, hogy a nevezőben lévő kifejezés pont ∂yF(x,y) és az implicit függvény létezésének feltétele pont a nevező nullától különböző volta.
Többváltozós eset
Ebben az esetben is az „érintősík” végtelenül közelítő tulajdonsága játszik majd fontos szerepet. Jól látható az összefüggés, ha feltesszük, hogy F egy Rn×Rm-en értelmezett affin függvény, azaz egy lineáris leképezés eltoltja. Ekkor
- F(x,y) = F(a+h,b+k) = F(a,b)+dF1(a,b)h+dF2(a,b)k.
Amennyiben y = y(x) olyan, hogy y(a) = b és F(x,y(x)) = 0, akkor fennáll a 0 = dF1(a,b)h + dF2(a,b)k egyenlőség és k kifejezhető, amennyiben az A = dF2(a,b) mátrix invertálható. A B = dF1(a,b) jelöléssel ekkor
- k = -(A-1
 B) h.
B) h.
Általános esetben ez csak egy másodrendűen kicsiny tag hozzávételével lesz igaz, de az implicit függvény létezésének belátásához szükséges a fenti gondolatmenet is.
Banach-terek esetén (melyek akár végtelen dimenziósak is lehetnek) a tétel a következő.
Tétel – Implicitfüggvény-tétel Banach-terekre – Legyen E, H, G Banach-terek, F:E × H  G olyan függvény, mely (a,b) ∈ E × H-ban erősen differenciálható. Ha a ∂2F(a,b) lineáris leképezés injektív és az inverzével együtt folytonos, akkor egyértelműen létezik az F-nek egy az (a,b) párhoz tartozó f lokális implicit függvénye, ez erősen differenciálható a-ban és differenciálja:
G olyan függvény, mely (a,b) ∈ E × H-ban erősen differenciálható. Ha a ∂2F(a,b) lineáris leképezés injektív és az inverzével együtt folytonos, akkor egyértelműen létezik az F-nek egy az (a,b) párhoz tartozó f lokális implicit függvénye, ez erősen differenciálható a-ban és differenciálja:
Vagy egy kevésbé absztrakt tétel:
Tétel – Implicitfüggvény-tétel Rn-re – Legyen F:Rn×Rm Rm folytonosan differenciálható függvény, (a,b) ∈ Rn×Rmolyanok, hogy F(a,b)=0 és
Rm folytonosan differenciálható függvény, (a,b) ∈ Rn×Rmolyanok, hogy F(a,b)=0 és 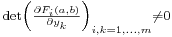 . Ekkor egyértelműen létezik F-nek egy az (a,b)-hez tartozó lokális implicit függvénye.
. Ekkor egyértelműen létezik F-nek egy az (a,b)-hez tartozó lokális implicit függvénye.
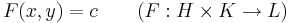
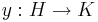
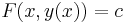
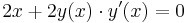
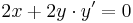
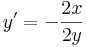
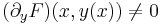
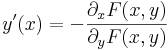
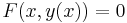
![[dF(x,y(x))]\cdot[1,y'(x)]=0\,](/upload/math/0/3/d/03df0c88cc92f15903dbacb24d470b40.png)
![[(\partial_x F)(x,y(x)),(\partial_y F)(x,y(x))]\cdot[1,y'(x)]=0\,](/upload/math/7/c/a/7ca9eceb268ea492e5c5dd4aa9f13282.png)
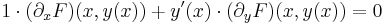
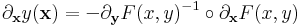
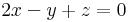

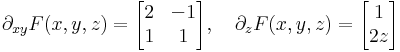
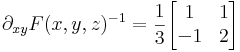
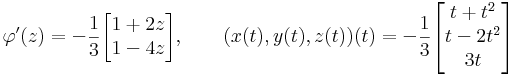
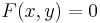
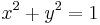
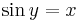
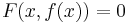
![\varphi'(u)=[\partial_1F(u,v),\partial_2F(u,v)]\cdot \begin{bmatrix}1\\f'(u)\end{bmatrix}=\partial_1 F(u,v)+\partial_2F(u,v)\cdot f'(u)\,=0](/upload/math/b/3/5/b359ce481428a0c89ae0f20fc230e3dc.png)